视觉slam14讲——第7讲 视觉里程计1
本系列文章是记录学习高翔所著《视觉slam14讲》的内容总结,文中的主要文字和代码、图片都是引用自课本和高翔博士的博客。代码运行效果是在自己电脑上实际运行得出。手动记录主要是为了深入理解
文章目录
- 第7讲 视觉里程计1
- 1 特征点法
- 1.1 人工设计的特征点有四个特征
- 1.2 特征点组成:
- 1.3 常见的特征点
- 2 ORB特征点
- 2.1 改进的FAST 关键点(Oriented FAST)
- 2.2 BRIEF描述子
- 2.3 特征匹配
- 2.3.1 存在的问题
- 2.3.2 匹配方法
- 2.4 特征提取和匹配代码实践的步骤分析
- 3 2D-2D对极几何
- 3.1 本质矩阵(Essential Matrix)$E$
- 3.2 单应矩阵H(Homography)
- 3.3 对极约束求相机运动代码实践
- 3.4 总结
- 4 三角测量(Triangulation)
- 4.1 三角测量理论介绍
- 4.2 三角测量代码实践
- 4.3 三角测量的矛盾
- 5 3D-2D : PnP
- 5.1 $PnP$简介
- 5.2 $PnP$求解——直接线性变换($DLT$)
- 5.3 $PnP$求解——$P3P$
- 5.3.1 $P3P$原理
- 5.3.2 $P3P$ 存在问题
- 5.4 $PnP$求解——Bundle Adjustment
- 5.5 $PnP$求解代码实践
- 5.5.1 使用$EPnP$求解位姿
- 5.5.2 使用$Bundle Adjustment$优化求解位姿
- 6 3D-3D:ICP估计相机位姿
- 6.1 求解ICP——SVD方法
- 6.2 求解ICP——非线性优化方法
- 6.3 代码实践
- 6.3.1 求解ICP——SVD方法代码实践
- 6.3.2 求解ICP——非线性方法代码实践
第7讲 视觉里程计1
这一讲笔记记录的主要下面几条内容
- 1 特征点如何提取并且匹配
- 2 利用对极约束方法从 2 D − 2 D 2D-2D 2D−2D匹配好的特征点估计相机运动
- 3 使用三角测量方法从 2 D − 2 D 2D-2D 2D−2D匹配估计一个点的空间位置
- 4 3 D − 2 D 3D-2D 3D−2D的 P n P PnP PnP问题的线性解法和 B o u n d A d j u s t m e n t Bound Adjustment BoundAdjustment解法
- 5 3 D − 3 D 3D-3D 3D−3D的 I C P ICP ICP问题的线性解法和 B o u n d A d j u s t m e n t Bound Adjustment BoundAdjustment解法
做了一个简单的流程图概括上述内容
1 特征点法
1.1 人工设计的特征点有四个特征
- 可重复性Repeatability
- 可区别性Distinctiveness
- 高效率Efficiency
- 本地性Locality
1.2 特征点组成:
- 关键点Key-Point
- 描述子Descriptor
外观相似的特征具有相似的描述子
1.3 常见的特征点
- SIFT 尺度不变特征变换
- SURF
- ORB 具有代表性的实时图像特征
2 ORB特征点
提取ORB特征的两个步骤:
- FAST角点提取
- BRIEF描述子
2.1 改进的FAST 关键点(Oriented FAST)
FAST是一种角点,主要检测局部像素灰度变化明显的地方,以速度快著称。它的一个思想是:如果一个像素与邻域像素的差别较大(过亮或过暗),那么它更可能是角点。
改进的FAST 关键点添加了方向和尺度信息。尺度不变性由构建图像金字塔,并在金字塔的每一层上检测角点来实现。而特征的旋转由灰度质心法来表示,步骤如下
(1) 定义图像块的矩 m p q = ∑ x p y q I ( x , y ) , p , q = 0 , 1 m_{pq}=\sum x^py^qI(x,y), p,q=0,1 mpq=∑xpyqI(x,y),p,q=0,1
(2) 图像块的质心
C = ( m 10 m 00 , m 01 m 00 ) = ( ∑ x I ( x , y ) ∑ I ( x , y ) , ∑ y I ( x , y ) ∑ I ( x , y ) ) C=(\frac{m_{10}}{m_{00}},\frac{m_{01}}{m_{00}})=(\frac{\sum{xI(x,y)}}{\sum{I(x,y)}},\frac{\sum{yI(x,y)}}{\sum{I(x,y)}}) C=(m00m10,m00m01)=(∑I(x,y)∑xI(x,y),∑I(x,y)∑yI(x,y))
(3) 特征点方向
θ = a r c t a n ( m 01 m 10 ) = a r c t a n ( ∑ y I ( x , y ) ∑ x I ( x , y ) ) \theta=arctan(\frac{m_{01}}{m_{10}})=arctan(\frac{\sum{yI(x,y)}}{\sum{xI(x,y)}}) θ=arctan(m10m01)=arctan(∑xI(x,y)∑yI(x,y))
2.2 BRIEF描述子
**BRIEF(Binary Robust Independent Elementary Feature)**是二进制描述子,它的描述向量是由许多个0和1组成,这里的0和1编码了关键点附近的两个像素 p p p和 q q q的大小关系,如果 p > q p>q p>q,则取1;反之取0。
大体上按照某种概率分布,随机的挑选 p p p和 q q q的位置,最终选取128对这样的 p p p和 q q q构成128维向量。
这段话看的一知半解,高博士说阅读BRIEF论文或者OPENCV源码可以查看具体实现。
这是使用opencv算法,提取出的ORB特征点,
作者高翔博士关于特征提取的代码如下
//-- 读取图像
Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );
//-- 初始化
std::vector keypoints_1, keypoints_2;
Mat descriptors_1, descriptors_2;
#ifndef __OPENCV_2__
// used in OpenCV3
Ptr detector = ORB::create();
Ptr descriptor = ORB::create();
#else
// use this if you are in OpenCV2
Ptr detector = FeatureDetector::create ( "ORB" );
Ptr descriptor = DescriptorExtractor::create ( "ORB" );
#endif
Ptr matcher = DescriptorMatcher::create ( "BruteForce-Hamming" );
//-- 第一步:检测 Oriented FAST 角点位置
detector->detect ( img_1, keypoints_1 );
detector->detect ( img_2, keypoints_2 );
//-- 第二步:根据角点位置计算 BRIEF 描述子
descriptor->compute ( img_1, keypoints_1, descriptors_1 );
descriptor->compute ( img_2, keypoints_2, descriptors_2 );
Mat outimg1;
drawKeypoints( img_1, keypoints_1, outimg1, Scalar::all(-1), DrawMatchesFlags::DEFAULT );
imshow("ORB特征点", outimg1);
2.3 特征匹配
特征匹配解决了SLAM中的数据关联问题(data association),即确定当前帧的图像特征与前一帧的图像对应关系,通过描述子的差异判断哪些特征为同一个点。
2.3.1 存在的问题
由于场景图像中存在大量重复的纹理,使得描述特征非常相似,导致错误匹配广泛存在。
2.3.2 匹配方法
在图像 I t I_t It中提取到特征点 x t m , m = 1 , 2 , . . . M x_t^m,m=1,2,...M xtm,m=1,2,...M,在图像 I t + 1 I_{t+1} It+1中提取到特征点 x t + 1 n , n = 1 , 2 , . . . N x_{t+1}^n,n=1,2,...N xt+1n,n=1,2,...N,寻找这两个集合之间的对应关系就是使用暴力匹配方法(Brute-Force Matcher)。
对每一个特征点 x t m x_t^m xtm和所有的 x t + 1 n x_{t+1}^n xt+1n测量描述子的距离,然后排序,取最近的一个点作为匹配点。
描述子 距离表示两个特征之间的相似程度,在实际应用中取不同的距离度量范数。
- 浮点类型的描述子使用欧式距离度量
- 二进制类型描述子 ( e g : B R I E F ) (eg: BRIEF) (eg:BRIEF)使用汉明距离 ( H a m m i n g D i s t a n c e ) (Hamming Distance) (HammingDistance)作为度量。比如两个二进制串的汉明距离表示不同位的个数。
特征点数量过大时,暴力匹配算法不能满足slam实时性的要求,它的改进算法是快速最近邻算法 ( F L A N N ) (FLANN) (FLANN),更加适合匹配点数量极多的情况。这些算法已经成熟,都已经集成到 O p e n C V OpenCV OpenCV中。
所有匹配点对如下图
优化后匹配的点对
特征匹配的代码如下,这个部分是紧接这上面的特征点提取部分的代码的。
//-- 第三步:对两幅图像中的BRIEF描述子进行匹配,使用 Hamming 距离
vector matches;
//BFMatcher matcher ( NORM_HAMMING );
matcher->match ( descriptors_1, descriptors_2, matches );
//-- 第四步:匹配点对筛选
double min_dist = 10000, max_dist = 0;
//找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
for ( int i = 0; i < descriptors_1.rows; i++ )
{
double dist = matches[i].distance;
if ( dist < min_dist ) min_dist = dist;
if ( dist > max_dist ) max_dist = dist;
}
// 仅供娱乐的写法
min_dist = min_element( matches.begin(), matches.end(), [](const DMatch & m1, const DMatch & m2) {return m1.distance < m2.distance;} )->distance;
max_dist = max_element( matches.begin(), matches.end(), [](const DMatch & m1, const DMatch & m2) {return m1.distance < m2.distance;} )->distance;
printf ( "-- Max dist : %f \n", max_dist );
printf ( "-- Min dist : %f \n", min_dist );
//当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
std::vector< DMatch > good_matches;
for ( int i = 0; i < descriptors_1.rows; i++ )
{
if ( matches[i].distance <= max ( 2 * min_dist, 30.0 ) )
{
good_matches.push_back ( matches[i] );
}
}
//-- 第五步:绘制匹配结果
Mat img_match;
Mat img_goodmatch;
drawMatches ( img_1, keypoints_1, img_2, keypoints_2, matches, img_match );
drawMatches ( img_1, keypoints_1, img_2, keypoints_2, good_matches, img_goodmatch );
imshow ( "所有匹配点对", img_match );
imshow ( "优化后匹配点对", img_goodmatch );
2.4 特征提取和匹配代码实践的步骤分析
(1)读取图像
(2)初始化 std::vector< KeyPoint > 类型的特征点和 Mat 类型的描述子
(3)定义Ptr< FeatureDetector >类型的检测对象,使用这个detect去检测两个图像,然后返回值存储在刚才定义的 std::vector< KeyPoint> 类型的特征点。
定义Ptr< DescriptorExtractor >类型的特征点提取对象,使用这个descriptor,根据计算出的关键点,计算BRIEF描述子
(4)使用OpenCV中的huigui模块,将特征点画出来
(5) 定义Ptr< DescriptorMatcher > 类型的匹配对象,用这个matcher,输入刚刚计算出的描述子descriptors_1,descriptors_2,对两幅图片的BRIEF描述子进行匹配,返回为vector< DMatch > 类型的匹配对象matches.
(6)对匹配点进行筛选,找出匹配点之间最小距离和最大距离,也就是找到最相似和最不相似的两组点之间的距离。当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限。
(7) 绘制匹配结果
最后高翔博士的输出结果是如下
可以看到最近的两个量的匹配的距离是4,最远的匹配距离是95。当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限。
3 2D-2D对极几何
根据得到的若干对匹配点,就可以通过这些二位图像的对应关系,恢复出两帧图像摄像机的运动。
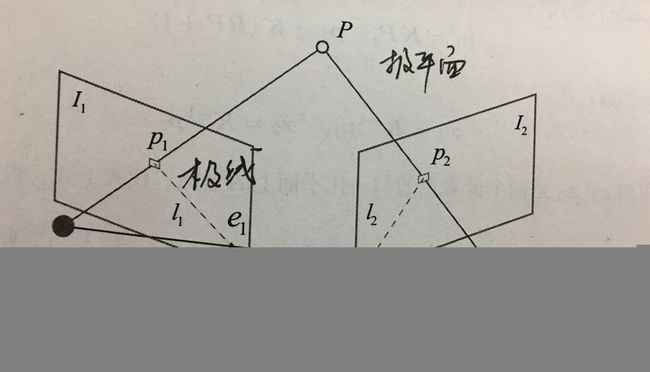
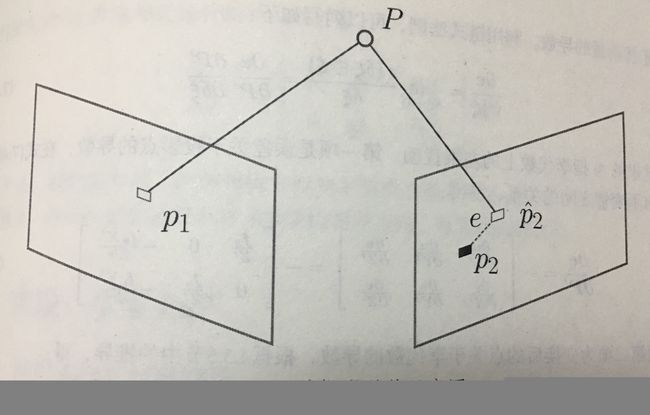
P P P为摄像机观察的空间的某一坐标点, p 1 , p 2 p_1,p_2 p1,p2为P在图像中的投影点,并且两幅图像较好的匹配到了, 最终推导出对极约束公式:
p 2 T K − T t ^ R K − 1 p 1 = 0 p_2^TK^{-T}t^{\hat{}}RK^{-1}p_1=0 p2TK−Tt^RK−1p1=0
定义中间部分的基础矩阵(Fundamental Matrix) F F F和本质矩阵(Essential Matrix) E E E
E = t ^ R , F = K − T t ^ R K − 1 E=t^{\hat{}}R, F=K^{-T}t^{\hat{}}RK^{-1} E=t^R,F=K−Tt^RK−1
也就得到 x 2 T E x 1 = p 2 T F p 1 x_2^TEx_1=p_2^TFp_1 x2TEx1=p2TFp1
对极约束给出了两个匹配点之间的空间关系,于是,问题简化为:
- 由匹配点的像素位置计算 E E E或者 F F F
- 由 E E E或 F F F求 R , t R,t R,t
3.1 本质矩阵(Essential Matrix) E E E
关于 E E E有三个特点
- 本质矩阵由对极约束定义,由于对极约束是等式为零的约束,所以对 E E E乘以乘任意非零常数依然满足,称 E E E在不同尺度下是等价的。
- KaTeX parse error: Got function '\hat' with no arguments as superscript at position 4: E=t^̲\hat{}R, E E E的奇异值(Singular Value)必定是 [ σ , σ , 0 ] T [\sigma, \sigma, 0]^T [σ,σ,0]T的形式,这称为本质矩阵 E E E的内在性质
- 由于平移旋转共6个自由度,所以KaTeX parse error: Got function '\hat' with no arguments as superscript at position 2: t^̲\hat{}R 有6个自由度。但是由于尺度等价性, E E E实际上共五个自由度
使用经典的八点法求解 E E E, 八点法构成的方程组可解出E, 还有一点需要注意的是下图,
八点法的总结:
- 用于单目视觉的初始化
- 尺度不确定性:归一化 t 或特征点的平均深度
- 纯旋转问题:t=0 时无法求解
- 多于八对点时:最小二乘或随机采样一致性(RANSAC)
3.2 单应矩阵H(Homography)
它描述的是两个平面之间的映射关系,如果场景中的特征点都落在同一平面上(比如情面、地面),则可以通过单应性进行运动估计。
假设特征点落在平面 P P P上,
n T P + d = 0 n^TP+d=0 nTP+d=0
也就是 − n T P d = 1 -\frac{n^TP}{d}=1 −dnTP=1
代入最开始式子 p 2 = K ( R P + t ) p_2=K(RP+t) p2=K(RP+t)
得到一个从图像坐标 p 1 p_1 p1到 p 2 p_2 p2之间的变换 p 2 = K ( R − t n T d ) K − 1 p 1 p_2=K(R-\frac{tn^T}{d})K^{-1}p_1 p2=K(R−dtnT)K−1p1
记作 p 2 = H p 1 p_2=Hp_1 p2=Hp1
它的定义与平移、旋转和平面的参数相关。
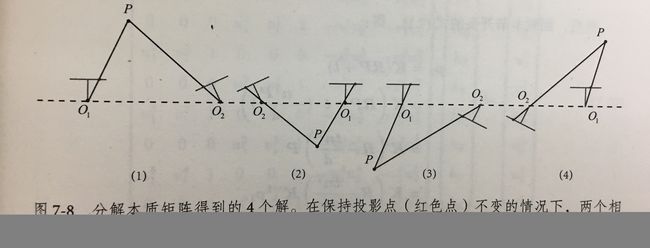
求解单应矩阵使用线性变换法(Direct Linear Transform), 与求解本质矩阵类似,求出来后需要对其进行分解才能得到 R , t R,t R,t,分解方法有数值法和解析法。分解同样得到四组解,最后根据先验信息进行排除得到唯一的一组 R , t R,t R,t解。
3.3 对极约束求相机运动代码实践
void pose_estimation_2d2d ( std::vector keypoints_1,
std::vector keypoints_2,
std::vector< DMatch > matches,
Mat& R, Mat& t )
{
// 相机内参,TUM Freiburg2
Mat K = ( Mat_ ( 3, 3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
//-- 把匹配点转换为vector的形式
vector points1;
vector points2;
for ( int i = 0; i < ( int ) matches.size(); i++ )
{
points1.push_back ( keypoints_1[matches[i].queryIdx].pt );
points2.push_back ( keypoints_2[matches[i].trainIdx].pt );
}
//-- 计算基础矩阵
Mat fundamental_matrix;
fundamental_matrix = findFundamentalMat ( points1, points2, CV_FM_8POINT );
cout << "fundamental_matrix is " << endl << fundamental_matrix << endl;
//-- 计算本质矩阵
Point2d principal_point ( 325.1, 249.7 ); //相机光心, TUM dataset标定值
double focal_length = 521; //相机焦距, TUM dataset标定值
Mat essential_matrix;
essential_matrix = findEssentialMat ( points1, points2, focal_length, principal_point );
cout << "essential_matrix is " << endl << essential_matrix << endl;
//-- 计算单应矩阵
Mat homography_matrix;
homography_matrix = findHomography ( points1, points2, RANSAC, 3 );
cout << "homography_matrix is " << endl << homography_matrix << endl;
//-- 从本质矩阵中恢复旋转和平移信息.
recoverPose ( essential_matrix, points1, points2, R, t, focal_length, principal_point );
cout << "R is " << endl << R << endl;
cout << "t is " << endl << t << endl;
}
演示了如何使用2D-2D的特征匹配估计相机运动代码如下
//-- 读取图像
Mat img_1 = imread ( argv[1], CV_LOAD_IMAGE_COLOR );
Mat img_2 = imread ( argv[2], CV_LOAD_IMAGE_COLOR );
vector keypoints_1, keypoints_2;
vector matches;
find_feature_matches ( img_1, img_2, keypoints_1, keypoints_2, matches );
cout << "一共找到了" << matches.size() << "组匹配点" << endl;
//-- 估计两张图像间运动
Mat R, t;
pose_estimation_2d2d ( keypoints_1, keypoints_2, matches, R, t );
//-- 验证E=t^R*scale
Mat t_x = ( Mat_ ( 3, 3 ) <<
0, -t.at ( 2, 0 ), t.at ( 1, 0 ),
t.at ( 2, 0 ), 0, -t.at ( 0, 0 ),
-t.at ( 1.0 ), t.at ( 0, 0 ), 0 );
cout << "t^R=" << endl << t_x*R << endl;
//-- 验证对极约束
Mat K = ( Mat_ ( 3, 3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
for ( DMatch m : matches )
{
Point2d pt1 = pixel2cam ( keypoints_1[ m.queryIdx ].pt, K );
Mat y1 = ( Mat_ ( 3, 1 ) << pt1.x, pt1.y, 1 );
Point2d pt2 = pixel2cam ( keypoints_2[ m.trainIdx ].pt, K );
Mat y2 = ( Mat_ ( 3, 1 ) << pt2.x, pt2.y, 1 );
Mat d = y2.t() * t_x * R * y1;
cout << "epipolar constraint = " << d << endl;
}
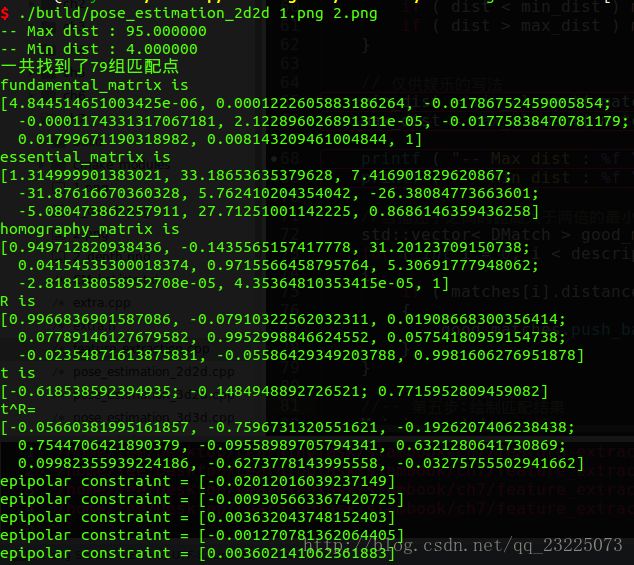
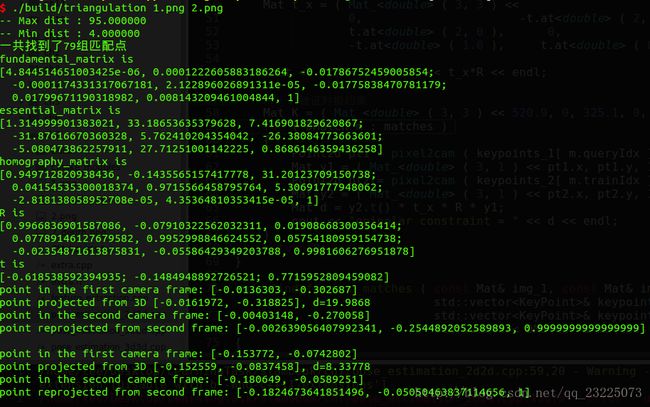
最后程序执行结果如下
观察结果可以看到验证对极约束的精度在小数点后三位 1 0 − 3 10^{-3} 10−3。
3.4 总结
-
尺度不确定性
对 t t t长度的归一化,直接导致单目视觉的尺度不确定性(Scale Ambiguity),在单目视觉中对两张图像的 t t t归一化相当于固定了制度,我们不知道长度是多少,但是我们这是 t t t的单位是1,计算相机运动和特征点的 3 D 3D 3D的位置,这被称为单目视觉SLAM的初始化。 -
初始化的纯旋转问题
单目视觉初始化不能只有纯旋转,必须要有一定程度的平移。如果没有平移,从 E E E分解到 R , t R,t R,t的过程中,导致 t t t为零,那么得到的 E E E也为零,这将导致无法求解 R R R。不过此时可以依靠 H H H求取旋转,但是仅仅有旋转时,无法使用三角测量估计特征点的空间位置。 -
对于8对点的情况
当给定匹配点多余8个的时候,比如算出79对匹配点,使用一个最小二乘计算 m i n e ∣ ∣ A e ∣ ∣ 2 2 = m i n e e T A T A e \underset{e}{min}||Ae||^2_2=\underset{e}{min \quad} e^TA^TAe emin∣∣Ae∣∣22=emineTATAe, 不过在存在错误匹配的情况下使用随机抽样一致算法(Random Sample Concensus,RANSAC),可以处理带有错误匹配的数据。 -
单应矩阵和本质矩阵使用情景区别
- 单应矩阵用于场景的特征点都落在同一个平面上的时候使用,比如墙,地面,可以通过单应性来估计运动,因为当特征点共面的时候,基础矩阵的自由度下降也就是出现退化现象
- 本质矩阵用于估计特征点不共面的情况下
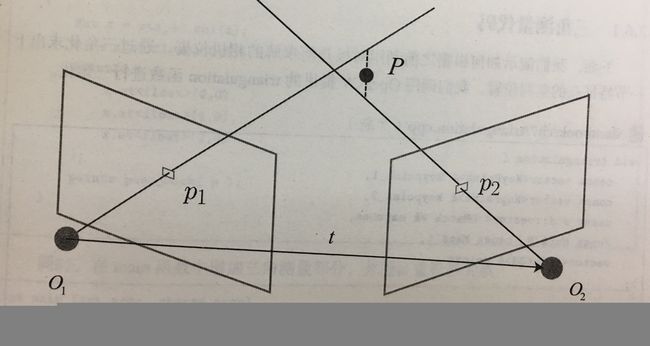
4 三角测量(Triangulation)
4.1 三角测量理论介绍
上一步得到运动之后,下一步需要用相机的运动估计特征点的空间位置。
三角测量指的是通过在两处观察同一个点的夹角,从而确定改点的距离。最早是由高斯提出的。由于噪声的影响,图中的两条直线无法相交,因此可以通过最小二乘求解。
按照对极几何的定义,设 x 1 , x 2 x_1,x_2 x1,x2为两个特征点归一化坐标,满足 s 1 x 1 = s 2 R x 2 + t s_1x_1=s_2Rx_2+t s1x1=s2Rx2+t
现在 R , t R,t R,t是已知的,需要求解深度信息 s 1 , s 2 s_1,s_2 s1,s2,先对上个式子两侧左乘 x 1 ^ x_1^{\hat{}} x1^,得到 s 1 x 1 ^ x 1 = 0 = s 2 x 1 ^ R x 2 + t s_1x_1^{\hat{}}x_1=0=s_2x_1^{\hat{}}Rx_2+t s1x1^x1=0=s2x1^Rx2+t
由此算出 s 2 s_2 s2,然后代入求出 s 1 s_1 s1
4.2 三角测量代码实践
void triangulation (
const vector< KeyPoint >& keypoint_1,
const vector< KeyPoint >& keypoint_2,
const std::vector< DMatch >& matches,
const Mat& R, const Mat& t,
vector< Point3d >& points )
{
Mat T1 = (Mat_ (3, 4) <<
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, 1, 0);
Mat T2 = (Mat_ (3, 4) <<
R.at(0, 0), R.at(0, 1), R.at(0, 2), t.at(0, 0),
R.at(1, 0), R.at(1, 1), R.at(1, 2), t.at(1, 0),
R.at(2, 0), R.at(2, 1), R.at(2, 2), t.at(2, 0)
);
Mat K = ( Mat_ ( 3, 3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
vector pts_1, pts_2;
for ( DMatch m : matches )
{
// 将像素坐标转换至相机坐标
pts_1.push_back ( pixel2cam( keypoint_1[m.queryIdx].pt, K) );
pts_2.push_back ( pixel2cam( keypoint_2[m.trainIdx].pt, K) );
}
Mat pts_4d;
cv::triangulatePoints( T1, T2, pts_1, pts_2, pts_4d );
// 转换成非齐次坐标
for ( int i = 0; i < pts_4d.cols; i++ )
{
Mat x = pts_4d.col(i);
x /= x.at(3, 0); // 归一化
Point3d p (
x.at(0, 0),
x.at(1, 0),
x.at(2, 0)
);
points.push_back( p );
}
}
验证三角化点与特征点的重投影关系代码如下,
//-- 验证三角化点与特征点的重投影关系
Mat K = ( Mat_ ( 3, 3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
for ( int i = 0; i < matches.size(); i++ )
{
Point2d pt1_cam = pixel2cam( keypoints_1[ matches[i].queryIdx ].pt, K );
Point2d pt1_cam_3d(
points[i].x / points[i].z,
points[i].y / points[i].z
);
cout << "point in the first camera frame: " << pt1_cam << endl;
cout << "point projected from 3D " << pt1_cam_3d << ", d=" << points[i].z << endl;
// 第二个图
Point2f pt2_cam = pixel2cam( keypoints_2[ matches[i].trainIdx ].pt, K );
Mat pt2_trans = R * ( Mat_(3, 1) << points[i].x, points[i].y, points[i].z ) + t;
pt2_trans /= pt2_trans.at(2, 0);
cout << "point in the second camera frame: " << pt2_cam << endl;
cout << "point reprojected from second frame: " << pt2_trans.t() << endl;
cout << endl;
}
结果显示了每个空间点在两个相机坐标系下的投影坐标和像素坐标,相当于 P P P的投影位置与看到的特征点的位置。由于误差存在,有微小差异。
point in the first camera frame: [-0.0136303, -0.302687]
point projected from 3D [-0.0161972, -0.318825], d=19.9868
比如这一对结果显示三角化特征点距离为19.9868,但是并不知道它代表多少米。
4.3 三角测量的矛盾
5 3D-2D : PnP
5.1 P n P PnP PnP简介
P n P PnP PnP(Perspective-n-Point)是求解3D到2D点对运动的方法。如果两张图像中其中一张特征点的3D位置已知,那么只需要3个点对便可以估计相机运动。
其中,特征点的3D位置可以由三角化或者RGB-D相机深度图获得。
单目双目使用 P n P PnP PnP的区别如下:
- 双目相机或者RGB-D相机的视觉里程计中可以使用 P n P PnP PnP估计相机运动
- 单目视觉需要先进性初始化,然后才能使用 P n P PnP PnP
解决 P n P PnP PnP问题的方法:
- 3对点估计位姿的 P 3 P P3P P3P
- 直接线性变换 D L T DLT DLT
- E P n P ( E f f i c i e n t P n P ) EPnP(Efficient PnP) EPnP(EfficientPnP)
- U P n P UPnP UPnP
- 非线性优化构建最小二乘并迭代求解(Bundle Adjustment)
5.2 P n P PnP PnP求解——直接线性变换( D L T DLT DLT)
最少通过6对匹配点实现矩阵 T T T的线性求解,当匹配点多于6对时,可以使用 S V D SVD SVD对超定方程求最小二乘解。
在 D L T DLT DLT中,将 T T T看做12个未知数,忽略之间的联系,求解出的 R R R不一定满足 S ( O 3 ) S(O3) S(O3)约束。对于旋转矩阵,必须针对 D L T DLT DLT估计的 T T T左边 3 × 3 3×3 3×3的矩阵块,寻找一个最好的旋转矩阵进行近似,可以使用 Q R QR QR分解完成。相当于把结果从矩阵空间投影到 S E ( 3 ) SE(3) SE(3)流形上。
5.3 P n P PnP PnP求解—— P 3 P P3P P3P
5.3.1 P 3 P P3P P3P原理
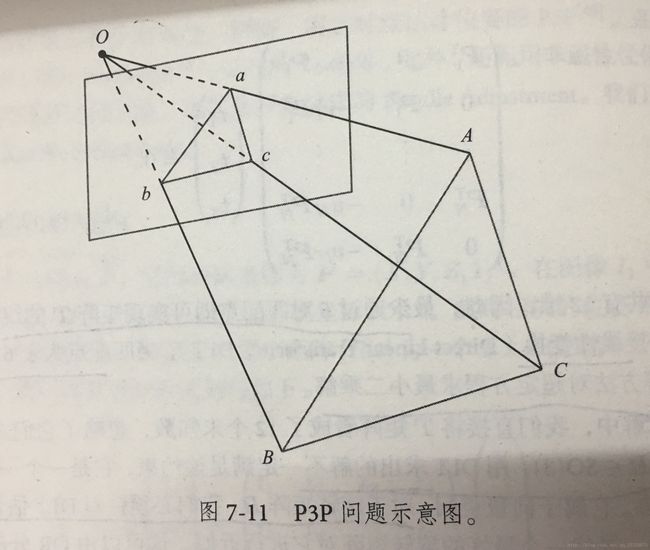
P 3 P P3P P3P利用3个点的几何关系(三角形的相似性),输入数据为3对 3 D − 2 D 3D-2D 3D−2D匹配点, 3 D 3D 3D点是 A , B , C A,B,C A,B,C(世界坐标系中坐标), 2 D 2D 2D点是 a , b , c a,b,c a,b,c(成像平面像素坐标)。此外 P 3 P P3P P3P还需要一对验证点,从可能解中选出正确的哪一个(类似于对极几何)。记验证点对为 D − d D-d D−d。
输出数据是得到 A , B , C A,B,C A,B,C在相机坐标系下的 3 D 3D 3D坐标。
这样就得到了 3 D − 3 D 3D-3D 3D−3D对应点,此时转换成了 I C P ICP ICP问题。
5.3.2 P 3 P P3P P3P 存在问题
- P 3 P P3P P3P只利用3个点的信息,当给定匹配点多余3组时,难以利用更多信息
- 如果 3 D 3D 3D点或者 2 D 2D 2D点受噪声影响,或者存在误匹配,算法失效
后续人们提出的 E P n P ( E f f i c i e n t P n P ) EPnP(Efficient PnP) EPnP(EfficientPnP), U P n P UPnP UPnP就是利用更多的信息,而且使用迭代的方式对相机位姿进行优化,尽可能消除噪声的影响。
在 S L A M SLAM SLAM中,通常先使用 P 3 P / E P n P P3P/EPnP P3P/EPnP等方法估计相机位姿,然后构建最小二乘优化问题对估计值进行调整(Bundle Adjustment) 。
5.4 P n P PnP PnP求解——Bundle Adjustment
除了使用线性方法之外,还可以把 P n P PnP PnP问题构建成一个定义于李代数上的非线性最小二乘问题。
- 线性方法:先求相机位姿,再求空间点位置
- 非线性优化方法:把他们都看成优化变量,放在一起进行优化。这是一种非常通用的求解方法。
在 P n P PnP PnP中这个Bundle Adjustment问题是一个最小化重投影误差(Reprojection error)的问题。
像素与空间点位置关系是 s i u i = K e x p ( ξ ^ ) P i s_iu_i=Kexp(\xi^{\hat{}})P_i siui=Kexp(ξ^)Pi
把误差求和构建最小二乘问题,然后寻找最好的相机位姿,使其最小化
ξ ∗ = a r g m i n ξ 1 2 ∑ i = 1 n ∣ ∣ u i − 1 s i K e x p ( ξ ^ ) P i ∣ ∣ 2 2 \xi^{*}=arg\space \underset{\xi}{min}\frac{1}{2}\sum_{i=1}^{n}||u_i-\frac{1}{s_i}Kexp(\xi^{\hat{}})P_i||_2^2 ξ∗=arg ξmin21i=1∑n∣∣ui−si1Kexp(ξ^)Pi∣∣22
该问题的误差项是将像素坐标(观测到的投影位置)与 3 D 3D 3D点按照当前估计的相机位姿进行投影得到的位置相比较得到的误差,称为重投影误差。
5.5 P n P PnP PnP求解代码实践
5.5.1 使用 E P n P EPnP EPnP求解位姿
利用 O p e n C V OpenCV OpenCV提供的 E P n P EPnP EPnP求解 P n P PnP PnP问题,然后通过 g 2 o g2o g2o对结果优化。
下面一段代码是在得到配对特征点后,在第一个图的深度图中寻找他们的深度,并求出空间位置。以此空间位置为3D点,在以第二个图的像素位置为2D点,调用 E P n P EPnP EPnP求解 P n P PnP PnP问题。
// 建立3D点
Mat d1 = imread ( argv[3], CV_LOAD_IMAGE_UNCHANGED ); // 深度图为16位无符号数,单通道图像
Mat K = ( Mat_ ( 3, 3 ) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1 );
vector pts_3d;
vector pts_2d;
for ( DMatch m : matches )
{
ushort d = d1.ptr (int ( keypoints_1[m.queryIdx].pt.y )) [ int ( keypoints_1[m.queryIdx].pt.x ) ];
if ( d == 0 ) // bad depth
continue;
float dd = d / 1000.0;
Point2d p1 = pixel2cam ( keypoints_1[m.queryIdx].pt, K );
pts_3d.push_back ( Point3f ( p1.x * dd, p1.y * dd, dd ) );
pts_2d.push_back ( keypoints_2[m.trainIdx].pt );
}
cout << "3d-2d pairs: " << pts_3d.size() << endl;
Mat r, t;
solvePnP ( pts_3d, pts_2d, K, Mat(), r, t, false ); // 调用OpenCV 的 PnP 求解,可选择EPNP,DLS等方法
Mat R;
cv::Rodrigues ( r, R ); // r为旋转向量形式,用Rodrigues公式转换为矩阵
cout << "R=" << endl << R << endl;
cout << "t=" << endl << t << endl;
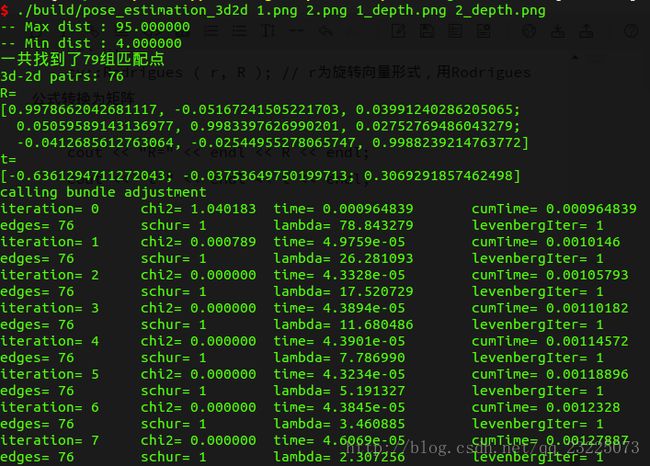
程序执行结果如下图
可以看到一共迭代了10次求出了最优解。
5.5.2 使用 B u n d l e A d j u s t m e n t Bundle Adjustment BundleAdjustment优化求解位姿
求解过程首先使用 C e r e s 或 者 g 2 o Ceres或者g2o Ceres或者g2o构建一个最小二乘问题。
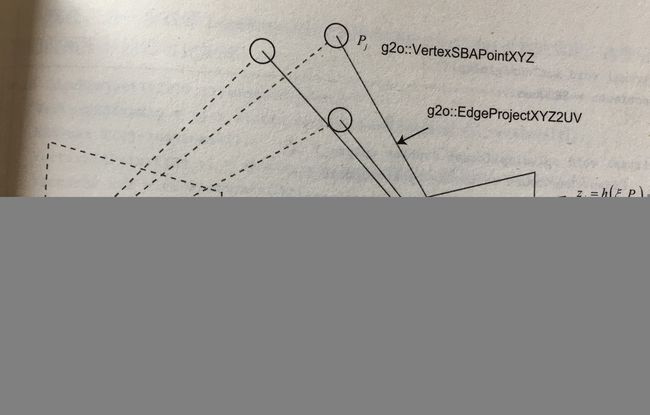
使用 g 2 o g2o g2o建模的图优化节点和边,图示如下
bundleAdjustment代码如下
void bundleAdjustment (
const vector< Point3f > points_3d,
const vector< Point2f > points_2d,
const Mat& K,
Mat& R, Mat& t )
{
// 初始化g2o
typedef g2o::BlockSolver< g2o::BlockSolverTraits<6, 3> > Block; // pose 维度为 6, landmark 维度为 3
Block::LinearSolverType* linearSolver = new g2o::LinearSolverCSparse(); // 线性方程求解器
Block* solver_ptr = new Block ( linearSolver ); // 矩阵块求解器
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg ( solver_ptr );
g2o::SparseOptimizer optimizer;
optimizer.setAlgorithm ( solver );
// vertex
g2o::VertexSE3Expmap* pose = new g2o::VertexSE3Expmap(); // camera pose
Eigen::Matrix3d R_mat;
R_mat <<
R.at ( 0, 0 ), R.at ( 0, 1 ), R.at ( 0, 2 ),
R.at ( 1, 0 ), R.at ( 1, 1 ), R.at ( 1, 2 ),
R.at ( 2, 0 ), R.at ( 2, 1 ), R.at ( 2, 2 );
pose->setId ( 0 );
pose->setEstimate ( g2o::SE3Quat (
R_mat,
Eigen::Vector3d ( t.at ( 0, 0 ), t.at ( 1, 0 ), t.at ( 2, 0 ) )
) );
optimizer.addVertex ( pose );
int index = 1;
for ( const Point3f p : points_3d ) // landmarks
{
g2o::VertexSBAPointXYZ* point = new g2o::VertexSBAPointXYZ();
point->setId ( index++ );
point->setEstimate ( Eigen::Vector3d ( p.x, p.y, p.z ) );
point->setMarginalized ( true ); // g2o 中必须设置 marg 参见第十讲内容
optimizer.addVertex ( point );
}
// parameter: camera intrinsics
g2o::CameraParameters* camera = new g2o::CameraParameters (
K.at ( 0, 0 ), Eigen::Vector2d ( K.at ( 0, 2 ), K.at ( 1, 2 ) ), 0
);
camera->setId ( 0 );
optimizer.addParameter ( camera );
// edges
index = 1;
for ( const Point2f p : points_2d )
{
g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
edge->setId ( index );
edge->setVertex ( 0, dynamic_cast ( optimizer.vertex ( index ) ) );
edge->setVertex ( 1, pose );
edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
edge->setParameterId ( 0, 0 );
edge->setInformation ( Eigen::Matrix2d::Identity() );
optimizer.addEdge ( edge );
index++;
}
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.setVerbose ( true );
optimizer.initializeOptimization();
optimizer.optimize ( 100 );
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration time_used = chrono::duration_cast> ( t2 - t1 );
cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
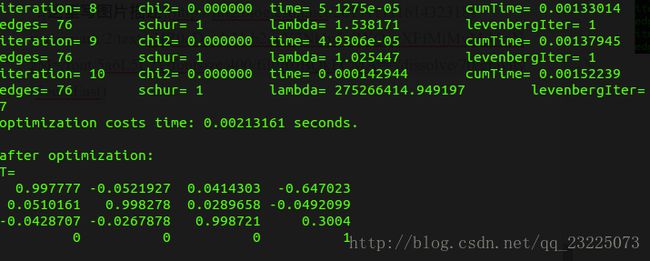
cout << endl << "after optimization:" << endl;
cout << "T=" << endl << Eigen::Isometry3d ( pose->estimate() ).matrix() << endl;
}
计算结果如上图。
6 3D-3D:ICP估计相机位姿
最后解决3D-3D位姿估计问题,也就是根据一组已经匹配好的3D点,
P = { p 1 , . . , p n } , P ′ = { p 1 ′ , . . , p n ′ } P=\{p_1,..,p_n\},P^{'}=\{p_1^{'},..,p_n^{'}\} P={p1,..,pn},P′={p1′,..,pn′}
从中找到一个欧氏变换的 R , t R,t R,t,使得
任 意 i 满 足 p i = R p i ′ + t 任意i满足p_i=Rp_i^{'}+t 任意i满足pi=Rpi′+t
这个问题是用迭代最近点(ICP)解决。和PnP类似,ICP有两种解法
- 线性代数求解(SVD方法)
- 非线性优化方法(类似于Bundle Adjustment)
6.1 求解ICP——SVD方法
目标函数建模如下
m i n R , t J = 1 2 ∑ i = 1 n ∣ ∣ p i − p − R ( p i ′ − p ′ ) ∣ ∣ 2 2 + ∣ ∣ p − R p i − t ) ∣ ∣ 2 2 \underset{R,t}{min}\space J=\frac{1}{2}\sum_{i=1}^{n}||p_i-p-R(p_i^{'}-p^{'})||_2^2+||p-Rp_i-t)||_2^2 R,tmin J=21i=1∑n∣∣pi−p−R(pi′−p′)∣∣22+∣∣p−Rpi−t)∣∣22
求解步骤如下
- 1 计算两组点的质心位置 p , p ′ p,p^{'} p,p′,然后计算每个点的去质心坐标
q i = p i = p , q i ′ = p i ′ − p ′ q_i=p_i=p,\space q_i^{'}=p_i^{'}-p^{'} qi=pi=p, qi′=pi′−p′- 2 根据一下优化问题计算旋转矩阵
R ∗ = a r g m i n R = 1 2 ∑ i = 1 n ∣ ∣ q i − R q i ′ ∣ ∣ 2 R^*=arg\space \underset{R}{min}=\frac{1}{2}\sum_{i=1}^{n}||q_i-Rq_i^{'}||^2 R∗=arg Rmin=21i=1∑n∣∣qi−Rqi′∣∣2- 3 根据第二步结果计算 t t t
t ∗ = p − R p ′ t^*=p-Rp^{'} t∗=p−Rp′
6.2 求解ICP——非线性优化方法
目标函数建模如下
m i n ξ = 1 2 ∑ i = 1 n ∣ ∣ p i − K e x p ( ξ ^ ) P i ′ ∣ ∣ 2 2 \underset{\xi}{min}=\frac{1}{2}\sum_{i=1}^{n}||p_i-Kexp(\xi^{\hat{}})P_i^{'}||_2^2 ξmin=21i=1∑n∣∣pi−Kexp(ξ^)Pi′∣∣22
可以证明ICP问题岑霭唯一解或无穷多解得情况。唯一解情况下,只要能找到极小值解,那么就是全局最优值——因此不会遇到局部极小值非全局最小值的情况。
这意味着ICP求解可以任意选定初始值,这是已经匹配点求解ICP问题的一个好处。
6.3 代码实践
6.3.1 求解ICP——SVD方法代码实践
void pose_estimation_3d3d (
const vector& pts1,
const vector& pts2,
Mat& R, Mat& t
)
{
Point3f p1, p2; // center of mass
int N = pts1.size();
for ( int i = 0; i < N; i++ )
{
p1 += pts1[i];
p2 += pts2[i];
}
p1 = Point3f( Vec3f(p1) / N);
p2 = Point3f( Vec3f(p2) / N);
vector q1 ( N ), q2 ( N ); // remove the center
for ( int i = 0; i < N; i++ )
{
q1[i] = pts1[i] - p1;
q2[i] = pts2[i] - p2;
}
// compute q1*q2^T
Eigen::Matrix3d W = Eigen::Matrix3d::Zero();
for ( int i = 0; i < N; i++ )
{
W += Eigen::Vector3d ( q1[i].x, q1[i].y, q1[i].z ) * Eigen::Vector3d ( q2[i].x, q2[i].y, q2[i].z ).transpose();
}
cout << "W=" << W << endl;
// SVD on W
Eigen::JacobiSVD svd ( W, Eigen::ComputeFullU | Eigen::ComputeFullV );
Eigen::Matrix3d U = svd.matrixU();
Eigen::Matrix3d V = svd.matrixV();
cout << "U=" << U << endl;
cout << "V=" << V << endl;
Eigen::Matrix3d R_ = U * ( V.transpose() );
Eigen::Vector3d t_ = Eigen::Vector3d ( p1.x, p1.y, p1.z ) - R_ * Eigen::Vector3d ( p2.x, p2.y, p2.z );
// convert to cv::Mat
R = ( Mat_ ( 3, 3 ) <<
R_ ( 0, 0 ), R_ ( 0, 1 ), R_ ( 0, 2 ),
R_ ( 1, 0 ), R_ ( 1, 1 ), R_ ( 1, 2 ),
R_ ( 2, 0 ), R_ ( 2, 1 ), R_ ( 2, 2 )
);
t = ( Mat_ ( 3, 1 ) << t_ ( 0, 0 ), t_ ( 1, 0 ), t_ ( 2, 0 ) );
}
6.3.2 求解ICP——非线性方法代码实践
Eigen::Matrix3d::Identity(),
Eigen::Vector3d( 0, 0, 0 )
) );
optimizer.addVertex( pose );
// edges
int index = 1;
vector edges;
for ( size_t i = 0; i < pts1.size(); i++ )
{
EdgeProjectXYZRGBDPoseOnly* edge = new EdgeProjectXYZRGBDPoseOnly(
Eigen::Vector3d(pts2[i].x, pts2[i].y, pts2[i].z) );
edge->setId( index );
edge->setVertex( 0, dynamic_cast (pose) );
edge->setMeasurement( Eigen::Vector3d(
pts1[i].x, pts1[i].y, pts1[i].z) );
edge->setInformation( Eigen::Matrix3d::Identity() * 1e4 );
optimizer.addEdge(edge);
index++;
edges.push_back(edge);
}
chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
optimizer.setVerbose( true );
optimizer.initializeOptimization();
optimizer.optimize(10);
chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
chrono::duration time_used = chrono::duration_cast>(t2 - t1);
cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
cout << endl << "after optimization:" << endl;
cout << "T=" << endl << Eigen::Isometry3d( pose->estimate() ).matrix() << endl;
}