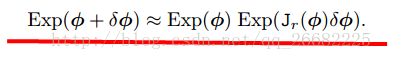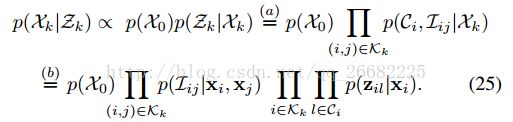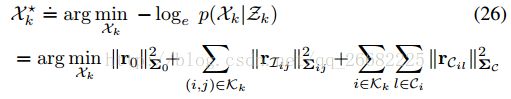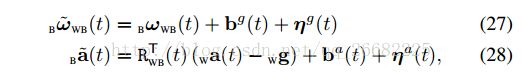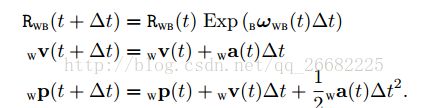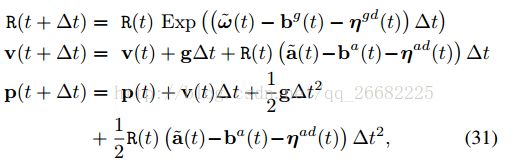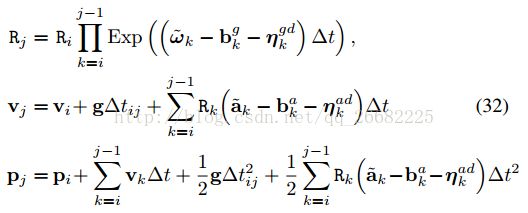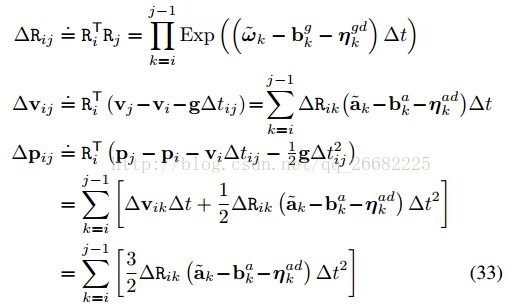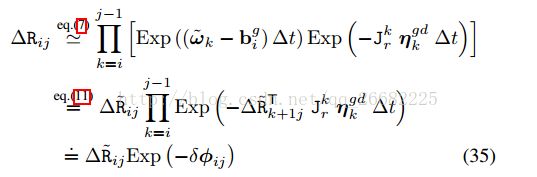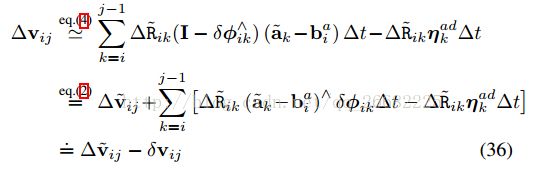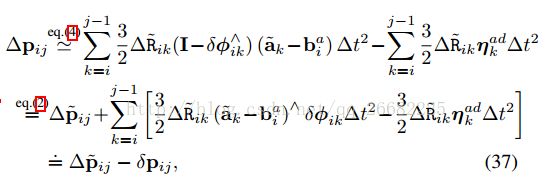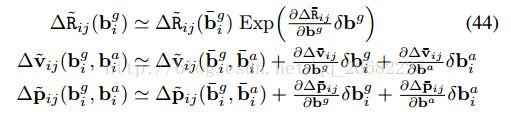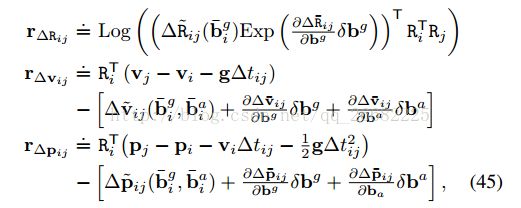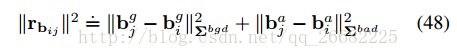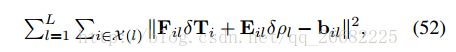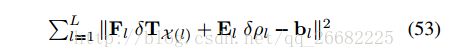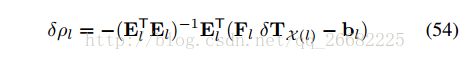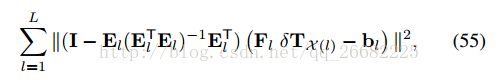paper阅读：流形上的预积分理论
看Forster的paper有两天了，今天想总结一下，好文章信息量总是很足的。
1.预积分的由来
为什么要预积分了，slam系统中为了减小优化求解器的负担，采用了关键帧策略，IMU的速率显然要快于关键帧的插入，它们之间的关系可以用论文中的这张图很好的表示。
紧耦合的方式就是把imu和图像的信息共同来估计状态量，所以如何协调两者之间的关系了，预积分干了这么一件事，通过重新参数化，把关键帧之间的IMU测量值积分成相对运动的约束，避免了因为初始条件变化造成的重复积分，在下一个关键帧到来之前先对IMU数据积分，谓之预积分，不知道是否这样理解，其实后面会讲到，预积分的值并不是真实测量值。论文的两大贡献：1.推导了SO3上的预积分理论 2. 证明了预积分理论可以整合到基于因子图的VIN系统优化框架下，从而避免了优化所有的点，这就是增量式因子图，这也是它和图优化的主要区别。
2. VIN相关理论
基于滤波的方法能够快速的推断当前的状态量，但是精度会随着线性化误差的累积而恶化，基于优化的完全平滑方法精度高一些，但计算量很大，固定滞后的平滑方法（滑动窗？）是一个折中。作者在论文中提出了把预积分理论整合到因子图中，从而实现了增量式平滑方法，这样可以避免线性化误差的累积同时为精度和效率的平衡提供一种优雅的解决方法。此外作者采用了structless model(边际化？)，这样可以不用延迟视觉信息的处理，同时可以多次线性化视觉测量模型。具体代码的实现整合在了gtsam4.0中，有待研究。
从三个维度上去理解当前主流方法。（1）参加估计的pose number。full smoothers：所有pose; fixed-lag: 滑动窗内的pose；filter: 最近的pose。（2）代表不确定性的方法。EKF: 协方差矩阵；信息滤波和smoothers: 信息矩阵。（3）测量模型被线性化的次数：standard EKF :1; smoothing appoach : 多次。
fixed-lag 和filter的方式相比对外点有更强的鲁棒性，fixed-lag在边际化的会使H矩阵变得稠密，为了保持稀疏性，需要丢掉一些测量点。此外两者都需要采用first estimate jacobian 来线性化，来保持系统能观性不变，否则会引入错误的信息，关于first estimate jacobian 以后再作总结。
full smoothing 对所有pose进行估计，能保证最高的精度但是计算效率低，目前除了采用keyframe外，采用增量式因子图，即只更新被测量值影响的一小部分区域。
3. 推导
3.1李代数
作者采用右乘雅克比进行推导，下面贴出几个重要的公式
右乘下的一阶展开
SO3上的伴随性质
作者采用了如下的扰动模型，没用采用SE3，从而避免了计算SE3上的指数映射
3.2 最大后验概率的VIN状态估计
状态量
IMU位姿 (Ri,pi)属于SE(3),速度 vi∈R3. IMU biases bi= [bg iba i]∈ R6, bg i,ba i∈R3 分别是陀螺仪和加速度计的偏置，共15维的向量
Xk=.{xi}i∈Kk.表示所有的关键帧的状态量
Zk=.{Ci,Iij}(i,j)∈Kk.表示所有观测，其中Ci是视觉测量，Iij是两个关键帧之间的IMU测量
t到t+dt的运动关系通过积分得到
结合IMU的测量方程得到
这里的ηgd是离散高斯白噪声，其方差
所以重新参数化，定义相对运动的增量式表达如下
特别注意这里的速度增量和位置增量都不是真实的物理值，这样定义是为了让积分和i时刻的状态独立
这样可以直接从IMU的测量值得到等式右边积分的结果
现在还需要处理这个积分中的bias和白噪声，以下推导假设bias在两个关键帧之间是不变的
先是处理白噪声
首先想办法把白噪声给分离出来，方便以后的MAP
运用SO3上的右乘一阶展开和伴随性质
其中，
，∆R˜ij = 
将其带入后两个式子得到
将这三个式子带回33得到分离出白噪声的扰动积分模型
扰动向量为
同样运用一阶泰勒展开可以得到扰动的近似分布和误差传递模型
可以发现。这里的扰动是白噪声的线性组合，因此协方差可以由白噪声的协方差计算得到，作者提到这个计算可以以一种迭代的方式进行
接着讨论bias，bias在迭代优化的过程中会发生改变，用时刻i的bi处的一阶泰勒展开来更新
这样就可以不用重新计算所有的预积分了
写到这里，终于可以得到一个包含了bias更新的残差的一阶泰勒展开了
bias 模型
bias的变化是一个随机游走的过程，可以用如下模型近似
将上式在ti到tj上积分得到
其中ηbgd是离散高斯白噪声，其协方差矩阵
这样残差项
可以加入到式26中
3.5 structureless modle for vision measurement
视觉测量的残差用重投影误差表示为
L表示所有的路标点，X(l)表示观测到该路标点的关键帧，上式对扰动进行一阶泰勒展开得到
b表示线性化后的误差项，将每个点的雅克比矩阵叠加，写成矩阵形式得到
注意到在给定位姿扰动的情况下，路标点的扰动是独立的，因此可以先把这部分算出来
带入到53可以得到一个只含有位姿扰动的残差函数
之前理解有误，这和边际化明显是不同的