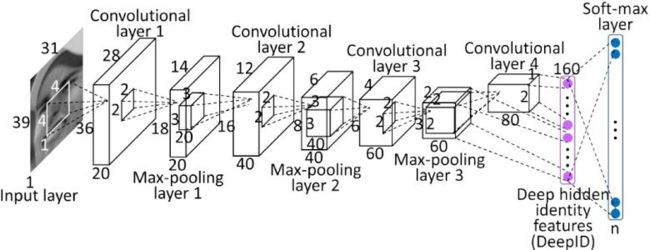
深度学习笔记------卷积神经网络
深度学习笔记------卷积神经网络
- 相关概念
- 卷积运算
- 互相关运算
- 稀疏交互
- 参数共享
- 卷积核
- 填充
- 步幅
- 多输入通道
- 多输出通道
- 层级分布
- 卷积层
- 归一化
- 整流(激活函数)
- 池化层
- 全连接层
相关概念
卷积运算
卷积函数: h ( x ) = ∫ f ( t ) g ( x − t ) d t h(x)=\int f(t)g(x-t)dt h(x)=∫f(t)g(x−t)dt
该函数定义了一种运算,对于 f , g f,g f,g两个函数进行,先将 g ( t ) g(t) g(t)进行一个反转运算于是 g ′ ( t ) = g ( − t ) g'(t)=g(-t) g′(t)=g(−t),之后在进行一个平移运算就变为了 g ′ ′ ( t ) = g ( x − t ) g''(t)=g(x-t) g′′(t)=g(x−t),之后就是两个函数的乘积积分,这就是对于一维的两个函数的卷积运算。
这个函数的来源是对于信号的处理上,用于描述系统的响应输出不仅与当前时刻x的输出有关,还与系统之前的响应有关,但是这个响应是会衰减的,于是当前时刻的实际输出响应是一个之前信号衰减函数与当前信号输出函数的积分运算,其中 g ( x − t ) g(x-t) g(x−t)中的x-t就是一个时间差的描述。
这个函数也有二维形式,也就是将其中的 f , g f,g f,g变为二元函数,对应的积分变为二重积分有:
h ( x , y ) = ∬ f ( v , u ) g ( x − v , y − u ) d v d u h(x,y)=\iint f(v,u)g(x-v,y-u)dvdu h(x,y)=∬f(v,u)g(x−v,y−u)dvdu
互相关运算
互相关函数: h ( x ) = ∫ f ( t ) g ( x + t ) d t h(x)=\int f(t)g(x+t)dt h(x)=∫f(t)g(x+t)dt
与上面的卷积相比,互相关函数并没有对 g ( x ) g(x) g(x)进行反转操作,剩下的就与卷积一致了。
对应反转与否在数学证明中是有影响的,决定了卷积运算的可交换性,但是在机器学习的训练中反转与否以及可交换性的影响就十分有限了,所以许多的卷积神经网络是实现的互相关运算,即没有反转,但是名字还是叫卷积。
进一步将互相关变为二维形式有: h ( x , y ) = ∬ f ( v , u ) g ( x + v , y + u ) d v d u h(x,y)=\iint f(v,u)g(x+v,y+u)dvdu h(x,y)=∬f(v,u)g(x+v,y+u)dvdu
再将积分变为累加有: ∑ ∑ f ( v , u ) g ( x + v , y + u ) \sum \sum f(v,u)g(x+v,y+u) ∑∑f(v,u)g(x+v,y+u)其中x与y为相应的偏移量,进一步细化,累加运算就是两个同形的矩阵对应元素的乘积和,于是便得到了我们熟悉的卷积层中的运算,其中进行偏移运算的函数 g g g称为核函数。
稀疏交互
卷积神经网络处理的大多为图像数据,如果仍旧使用神经网络中的全连接的话,相应的计算量会极其巨大,所以实际的核函数中的参数数量远小于输入单元的数量,用这种方式来代替全连接,可以减少相应的计算量与存储空间。
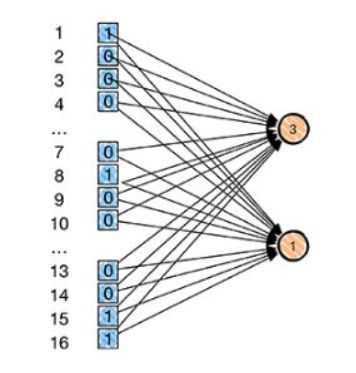
参数共享
还是相对于一般的神经网络而言,每一层的每一个输入到下一层之间都需要一个参数,而在卷积神经网络中,我们对核函数进行平移,每一次的平移相应的输入便会获得到一个参数进行运算,并将运算的结果传到下一层,所以在实际的运行中,模型维护的参数都在核函数中了,而核函数中的每一个参数通过卷积核在输入之间的平移进行共享,多个输入数据便可以共享同一个参数了。
卷积核
由上面的参数共享与稀疏交互,可以得知卷积神经网络的训练参数和全连接中的参数相比是有区别的,为了更好的体现数据间的空间关系,我们将这些训练参数以一个(多维)矩阵的方式(大多都是方阵)定义(是一个函数运算),并结合输入的数据来进行相关运算,用来获取输入数据的相关特征。
局部性: 由于稀疏交互与参数共享的要求,卷积核中的参数数量是远小于输入数据的,所以实际的运算中,卷积核运算后得到的结果是局部的特征。其局部的程度取决于卷积核的大小。
高维性: 由于我们输入的数据形式的多样,比如,图像是二维的,对图像进行rgb的处理后在二维上又会区分为三个通道变为三位的,所以卷积核的形式上也会随之进行维度的一致(保持与输入数据的深度一致)。
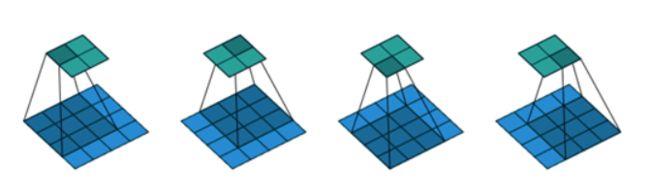
如图输入形状为 4 ∗ 4 4*4 4∗4,卷积核大小为 3 ∗ 3 3*3 3∗3
过滤器: 卷积核也叫过滤器,在卷积运算的过程中卷积核可以提取特定的特征,举个例子,现在有一个 3 ∗ 3 3*3 3∗3的卷积核 [ − 1 1 − 1 − 1 1 − 1 − 1 1 − 1 ] \begin{bmatrix}-1& 1 &-1 \\-1 & 1 &-1\\-1 & 1 & -1 \\\end{bmatrix} ⎣⎡−1−1−1111−1−1−1⎦⎤,其提取的对象是一个图片,对于与之进行运算的就是一个个 3 ∗ 3 3*3 3∗3的像素块了,那么相应的形状就是一个竖线,在图像中含有竖线部分比如: [ 1 0 0 0 1 0 0 1 0 ] \begin{bmatrix}1& 0 &0 \\0 & 1 &0\\0 & 1 & 0 \\\end{bmatrix} ⎣⎡100011000⎦⎤与 [ 0 1 0 0 1 0 0 1 0 ] \begin{bmatrix}0& 1 &0 \\0 & 1 &0\\0 & 1 & 0 \\\end{bmatrix} ⎣⎡000111000⎦⎤和 [ 1 1 1 1 1 1 1 1 1 ] \begin{bmatrix}1& 1 &1 \\1 & 1 &1\\1 & 1 & 1 \\\end{bmatrix} ⎣⎡111111111⎦⎤,在互相关运算之后得到的值为1,3,-3,越接近过滤器形状的像素块得到的值就越高,于是便实现了相关特征的提取。
填充
填充是在输入数据的两侧填充元素,一般对于二维的数据,是在每个维度的两侧填充,保证原有的数据位于中央。而填充的目的是为了控制输出的形状。
假设输入为 n h ∗ n w n_h*n_w nh∗nw,卷积核形状为 m h ∗ m w m_h*m_w mh∗mw,默认步幅为1,于是生成的输出形状为 ( n h − m h + 1 ) ∗ ( n w − m w + 1 ) (n_h-m_h+1)*(n_w-m_w+1) (nh−mh+1)∗(nw−mw+1)
假设在每个维度的两侧填充p行(列),于是原先的输入形状为 ( p + n h + p ) ∗ ( p + n w + p ) (p+n_h+p)*(p+n_w+p) (p+nh+p)∗(p+nw+p),输出就变为了 ( p + n h + p − m h + 1 ) ∗ ( p + n w + p − m w + 1 ) (p+n_h+p-m_h+1)*(p+n_w+p-m_w+1) (p+nh+p−mh+1)∗(p+nw+p−mw+1)
填充一般以常数0进行填充,由于卷积核的形状常常是奇数*奇数,所以一般在维度的两侧填充相同数量的常数。
步幅
在互相关或卷积运算中,会有一个相应的平移操作,对应的每次平移的数量就是步幅了,步幅与填充相结合可以控制输出时的形状,对于不同的维度可以设置不同的步幅.
假设宽上步幅为 s w s_w sw,高上的步幅为 s h s_h sh,按照之前的填充为 2 ∗ p 2*p 2∗p,于是实际的输出形状为 ⌊ ( p + n h + p − m h + s h ) / s h ⌋ ∗ ⌊ ( p + n w + p − m w + s w ) / s w ⌋ \lfloor(p+n_h+p-m_h+s_h)/s_h\rfloor*\lfloor(p+n_w+p-m_w+s_w)/s_w\rfloor ⌊(p+nh+p−mh+sh)/sh⌋∗⌊(p+nw+p−mw+sw)/sw⌋(向下取整)
填充可以增加输出的高和宽,步幅可以减少输出的高和宽。
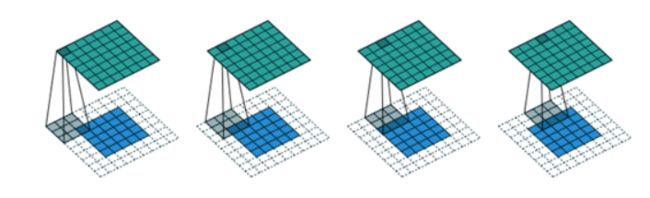
卷积核为 3 ∗ 3 3*3 3∗3,输入为 5 ∗ 5 5*5 5∗5,填充之后为 9 ∗ 9 9*9 9∗9,步幅为1。
卷积运算的过程实际就是卷积核窗口不断滑动计算的过程。
多输入通道
输入的数据是图片时,还会考虑不同颜色层级之间的关系,将原先的色彩分为rgb三色通道,有的时候还会有灰化处理,产生灰度图,所以输入的数据变为了三个维度,同样的为了对这些数据进行特征提取,我们的卷积核也要保持三维的。
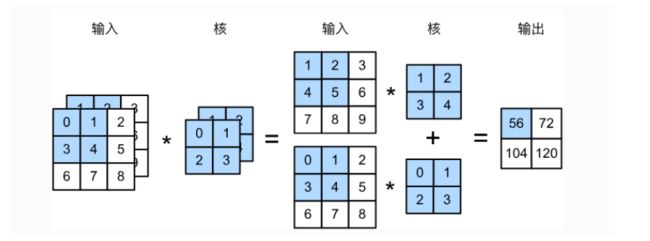
核函数与输入通道保持一致,每一个通道产生一个输出,最终将各个通道相加得到输出。
多输出通道
从上面的多输入通道可以了解,无论我们的输入数据的形状如何,在经过卷积核的处理后都会变为一个二维的输出(特征图)。一个卷积核对应了一个输出通道,我们可以设计多个卷积核构建出多个输出通道。

层级分布
卷积层
卷积层的输入一般为多维的数据,一般为二维或者三维的,除此之外就是相应的卷积核函数了,一般一个卷积层可能会包含多个卷积核函数,用来获得数据的不同特征,最后就是输出了,每一次的相关运算都会产生一个结果,这些数据保持原有数据的位置构成输出结果(即特征图),是具有相应特征的卷积核对原数据的特征提取,特征图的数量与卷积核的数量一致。
卷积运算或者是互相关运算构造的模型实质还是线性的,只不过相比于全连接,卷积层中的运算考虑到了数据的空间位置,将全连接中的一维变成了二维甚至多维。同样在卷积或者互相关操作之后,也需要加上相应的偏置值。
归一化
在实际的运用中,在完成卷积后与进行激活函数前,往往还需要进行归一化以防止在训练中出现梯度爆炸与梯度消失,所以在整流之前可以加一个归一化层,常用的有BN批标准化。
整流(激活函数)
同样的,在之前的卷积运算中与一般的神经网络一样仅只考虑了线性的部分,需要引入非线性的部分来提高模型的拟合能力,所以在卷积运算完成后需要通过非线性的激活函数,这里与一般的神经网络是一致的。
池化层
卷积层获得了卷积核处理之后的特征图,但是在这些数据中并不是都为相应的特征数据,有些边缘数据或者是不符合卷积核特征的数据是我们不需要的(特征数据并不是在任何位置都有),所以我们需要从处理过的数据中筛选出符合特征的数据(消除卷积层处理后对位置的敏感性,减少过拟合的可能),方便之后的判断,同时可以减少相应的无效数据,减小之后的计算压力。
与卷积运算相似,池化也需要一个窗口来划分一个范围,在这个范围中对数据进行筛选,并且这个窗口也可以进行移动,也有步幅与填充,相应的可以控制池化操作的输出数据尺寸。对于池化窗口的运算常用的有取最大值与取平均值,分别对应为最大池化层与平均池化层。
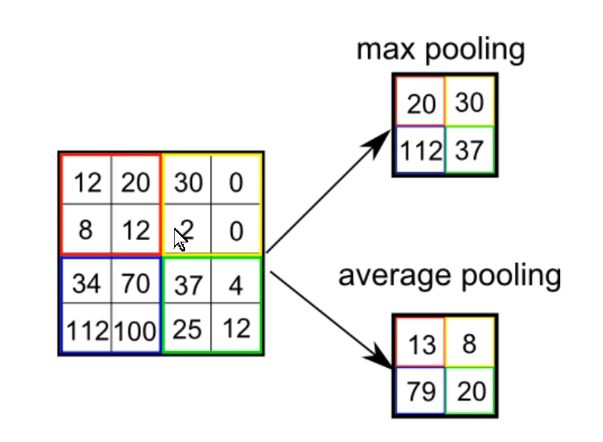
最大池化层: 从池化窗口中选出最大的值传到下一层,舍弃未选中的。
平均池化层: 将池化窗口中的平均值传到下一层。
多通道池化: 在处理多个特征图输入时,池化操作仅仅只是改变每个特征图的尺寸与其中的数据,具体的通道数量不变(不改变特征图的数量)。所以输入数据与输出数据的特征图个数一致。
全连接层
在多层次的卷积池化之后,可以看到数据量会不断减少,到最后会得到数量合适的数据,(但是还是多维的)将数据展开成为一维的数据,再对应到全连接的神经网路中进行训练,完成相应的分类或者预测处理。
在实际的应用中卷积神经网络会由多层的卷积与池化层组合,组合的过程中也不仅仅是在一维的线性中变化顺序,会有空间上的结构,多个层次的输出间会有分叉与交叉,训练的难度与实际的能力也会相应的提高。