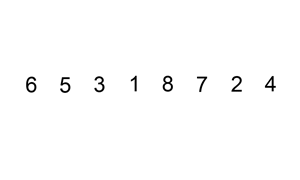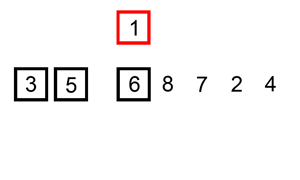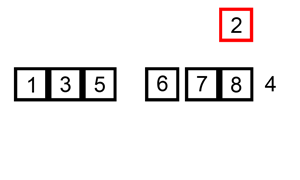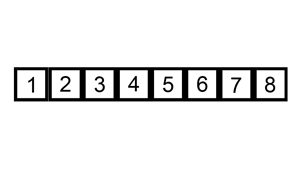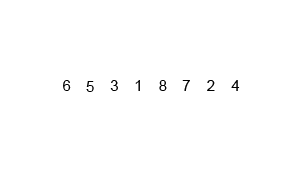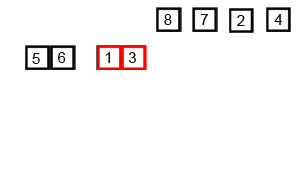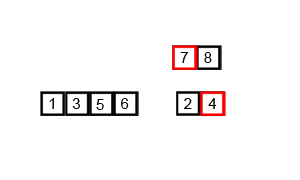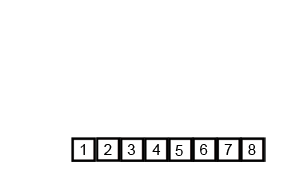Python 实现十大经典排序算法-LeetCode案例版
数据结构与算法-Python语言案例实现
- 十大经典排序算法
- 一、 引言
- 1.问题需求
- 2.方法分类
- 二、常见排序方法
- 1. 选择排序（Selection Sort）
- 2. 冒泡排序（Bubble Sort）
- 3. 插入排序（Insertion Sort）
- 4. 希尔排序（Shell Sort）
- 5. 归并排序（Merge Sort）
- 6. 快速排序（Quick Sort）
- 7. 堆排序（Heap Sort）
- 8. 计数排序（Counting Sort）
- 9. 桶排序（Bucket Sort）
- 10. 基数排序（Radix Sort）
- 三、算法总结
十大经典排序算法
一、 引言
授人以鱼不如授人以渔~
实践是检验真理的唯一标准~
算法与数据结构实战-LeetCode题解
1.问题需求
排序数组
给你一个整数数组 nums，请你将该数组升序排列。
或对一个无序数组，根据某个关键字排序。
示例 1：
输入：nums = [5,2,3,1]
输出：[1,2,3,5]
示例 2：
输入：nums = [5,1,1,2,0,0]
输出：[0,0,1,1,2,5]
Python语言实现
2.方法分类
排序算法划分方法有：稳定性，内外排序，时空复杂度
- 按照稳定性划分：稳定排序，如果a原本在b前面，而a=b，排序之后a仍然在b的前面；而不稳定可能出现在b之后
- 按照内外排序划分：内排序，所有排序操作都在内存中完成；外排序 ：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行
- 按照时空复杂度划分：时间复杂度是指运行时间，空间复杂度运行完一个程序所需内存的大小
二、常见排序方法
1. 选择排序（Selection Sort）
算法描述：
这应该最符合人类思维的排序方法，工作原理，首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。
稳定性：稳定；内排序
def selection_sort(nums):
n = len(nums)
for i in range(n):
for j in range(i, n):
if nums[i] > nums[j]:
nums[i], nums[j] = nums[j], nums[i]
return nums
# leetcode形式
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
# selection sort
n = len(nums)
for i in range(n):
for j in range(i,n):
if nums[i] > nums[j]:
nums[i],nums[j] = nums[j],nums[i]
#print(nums)
return nums
算法分析：
2. 冒泡排序（Bubble Sort）
算法描述：
冒泡排序时针对相邻元素之间的比较，可以将大的数慢慢“沉底”(数组尾部)
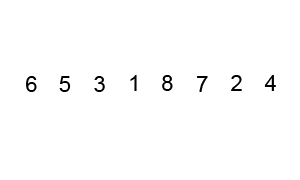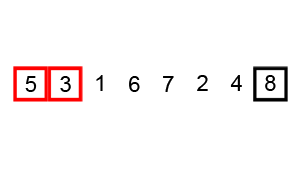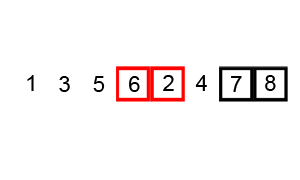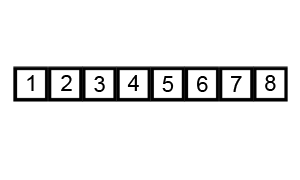
def bubble_sort(nums):
n = len(nums)
# 进行多次循环
for c in range(n):
for i in range(1, n - c):
if nums[i - 1] > nums[i]:
nums[i - 1], nums[i] = nums[i], nums[i - 1]
return nums
算法分析：
稳定排序，内排序，时间复杂度：
3. 插入排序（Insertion Sort）
算法描述：
插入排序是前面已排序数组找到插入的位置
def insertion_sort(nums):
n = len(nums)
for i in range(1, n):
while i > 0 and nums[i - 1] > nums[i]:
nums[i - 1], nums[i] = nums[i], nums[i - 1]
i -= 1
return nums
# LeetCode形式
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
# insert sort
n = len(nums)
for i in range(1,n):
while i > 0 and nums[i-1] > nums[i]:
nums[i-1],nums[i] = nums[i],nums[i-1]
i -= 1
return nums
算法分析：
稳定排序，内排序，时间复杂度：
4. 希尔排序（Shell Sort）
插入排序进阶版
算法描述：
def shell_sort(nums):
n = len(nums)
gap = n // 2
while gap:
for i in range(gap, n):
while i - gap >= 0 and nums[i - gap] > nums[i]:
nums[i - gap], nums[i] = nums[i], nums[i - gap]
i -= gap
gap //= 2
return nums
算法分析：
非稳定排序，内排序；
希尔排序的时间复杂度和增量序列是相关的。
5. 归并排序（Merge Sort）
归并排序，采用是分治法，先将数组分成子序列，让子序列有序，再将子序列间有序，合并成有序数组。
算法描述：
def merge_sort(nums):
if len(nums) <= 1:
return nums
mid = len(nums) // 2
# 分
left = merge_sort(nums[:mid])
right = merge_sort(nums[mid:])
# 合并
return merge(left, right)
def merge(left, right):
res = []
i = 0
j = 0
while i < len(left) and j < len(right):
if left[i] <= right[j]:
res.append(left[i])
i += 1
else:
res.append(right[j])
j += 1
res += left[i:]
res += right[j:]
return res
# LeetCode
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
res = []
mid = len(nums) //2
left, right = nums[:mid],nums[mid:]
if len(left) > 1: left = self.sortArray(left)
if len(right) > 1: right = self.sortArray(right)
while left and right:
if left[-1] >= right[-1]:
res.append(left.pop())
else:
res.append(right.pop())
res.reverse()
return (left or right) + res # 将剩余left或right中的数和res合并
算法分析：
稳定排序，外排序（占用额外内存），时间复杂度：O(nlogn)。
6. 快速排序（Quick Sort）
快速排序是选取一个“哨兵”(pivot)，将小于pivot放在左边，把大于pivot放在右边，分割成两部分，并且可以固定pivot在数组的位置，在对左右两部分继续进行排序。
快速排序使用分治法来把一个串（list）分为两个子串（sub-lists）。具体算法描述如下：
- 步骤1：从数列中挑出一个元素，称为 “基准”（pivot ）；
- 步骤2：重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
- 步骤3：递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。
def quick_sort(nums):
n = len(nums)
def quick(left, right):
if left >= right:
return nums
pivot = left
i = left
j = right
while i < j:
while i < j and nums[j] > nums[pivot]:
j -= 1
while i < j and nums[i] <= nums[pivot]:
i += 1
nums[i], nums[j] = nums[j], nums[i]
nums[pivot], nums[j] = nums[j], nums[pivot]
quick(left, j - 1)
quick(j + 1, right)
return nums
return quick(0, n - 1)
# LeetCode
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
n = len(nums)
first = 0
last = n - 1
self.quickSorthepler(nums,first,last)
return nums
def partition(self, alist, first, last):
left = first
right = last
pivot = alist[first]
while left < right:
while left < right and alist[right] >= pivot:
right -= 1
alist[left] = alist[right]
while left < right and alist[left] <= pivot:
left += 1
alist[right] = alist[left]
alist[left] = pivot
return left
def quickSorthepler(self, alist, first,last):
if first < last:
pointmark = self.partition(alist,first,last)
self.quickSorthepler(alist,first,pointmark-1)
self.quickSorthepler(alist, pointmark + 1, last)
算法分析：
不稳定排序，内排序，时间复杂度度O(nlogn)O(nlogn)。
7. 堆排序（Heap Sort）
堆排序是利用堆这个数据结构设计的排序算法。
算法描述：
- 建堆，从底向上调整堆，使得父亲节点比孩子节点值大，构成大顶堆；
- 交换堆顶和最后一个元素，重新调整堆。
调整堆方法写了递归和迭代，都很好理解！
def heap_sort(nums):
# 调整堆
# 迭代写法
def adjust_heap(nums, startpos, endpos):
newitem = nums[startpos]
pos = startpos
childpos = pos * 2 + 1
while childpos < endpos:
rightpos = childpos + 1
if rightpos < endpos and nums[rightpos] >= nums[childpos]:
childpos = rightpos
if newitem < nums[childpos]:
nums[pos] = nums[childpos]
pos = childpos
childpos = pos * 2 + 1
else:
break
nums[pos] = newitem
# 递归写法
def adjust_heap(nums, startpos, endpos):
pos = startpos
chilidpos = pos * 2 + 1
if chilidpos < endpos:
rightpos = chilidpos + 1
if rightpos < endpos and nums[rightpos] > nums[chilidpos]:
chilidpos = rightpos
if nums[chilidpos] > nums[pos]:
nums[pos], nums[chilidpos] = nums[chilidpos], nums[pos]
adjust_heap(nums, pos, endpos)
n = len(nums)
# 建堆
for i in reversed(range(n // 2)):
adjust_heap(nums, i, n)
# 调整堆
for i in range(n - 1, -1, -1):
nums[0], nums[i] = nums[i], nums[0]
adjust_heap(nums, 0, i)
return nums
# LeetCode
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
n = len(nums)
def build_heap(nums, start, end): # 建堆的同时调整堆
newitem = nums[start]
cur = start
leftpos = 2 * cur + 1
while leftpos < end:
rightpos = leftpos + 1
if rightpos < end and nums[rightpos] >= nums[leftpos]:
leftpos = rightpos
if newitem < nums[leftpos]:
nums[cur] = nums[leftpos]
cur = leftpos
leftpos = 2 * cur + 1
else:
break
nums[cur] = newitem
for i in reversed(range(n//2)): # 建堆+调整
build_heap(nums, i, n)
for i in range(n-1,-1,-1):
nums[0],nums[i] = nums[i],nums[0] #排序
build_heap(nums,0,i) #调整
return nums
# LeetCode
# 堆排序 递归写法
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
n = len(nums)
self.build_heap(nums,n)
print(nums)
for i in range(n-1,-1,-1):
nums[0],nums[i] = nums[i],nums[0] #排序
self.heapify(nums,0,i) #调整
return nums
# 递归写法
def heapify(self, nums, startpos, endpos):
if startpos >= endpos: return
c1 = startpos * 2 + 1
c2 = startpos * 2 + 2
max_index = startpos
if c1 < endpos and nums[c1] > nums[max_index]:
max_index = c1
if c2 < endpos and nums[c2] > nums[max_index]:
max_index = c2
if max_index != startpos:
nums[startpos], nums[max_index] = nums[max_index], nums[startpos]
self.heapify(nums, max_index, endpos)
def build_heap(self, nums, n):
last_node = n-1
parent = (last_node-1) // 2
for i in range(parent, -1,-1):
self.heapify(nums,i,n)
算法分析：
不稳定排序，内排序，时间复杂度为O(nlogn)O(nlogn)。
8. 计数排序（Counting Sort）
计数排序是典型的空间换时间算法，开辟额外数据空间存储用索引号记录数组的值和数组值个数
算法描述：
- 找出待排序的数组的最大值和最小值
- 统计数组值的个数
- 反向填充目标数组
def counting_sort(nums):
if not nums: return []
n = len(nums)
_min = min(nums)
_max = max(nums)
tmp_arr = [0] * (_max - _min + 1)
for num in nums:
tmp_arr[num - _min] += 1
j = 0
for i in range(n):
while tmp_arr[j] == 0:
j += 1
nums[i] = j + _min
tmp_arr[j] -= 1
return nums
# LeetCode
class Solution:
def sortArray(self, nums: List[int]) -> List[int]:
from collections import defaultdict
def counter_sort(nums,key=lambda x:x):
B,C = [], defaultdict(list)
for x in nums:
C[key(x)].append(x) # {1:1,2:2,......}
for k in range(min(C), max(C) + 1):
B.extend(C[k])
return B
res = counter_sort(nums)
return res
算法分析：
稳定排序，外排序，时间复杂度O(n + k)，但是对于数据范围很大的数组，需要大量时间和内存。
9. 桶排序（Bucket Sort）
桶排序是计数排序的升级版，原理是：输入数据服从均匀分布的，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的算法或是以递归方式继续使用桶排序，此文编码采用递归方式）
算法描述：
- 人为设置一个桶的BucketSize，作为每个桶放置多少个不同数值（意思就是BucketSize = 5，可以放5个不同数字比如[1, 2, 3,4,5]也可以放 100000个3，只是表示该桶能存几个不同的数值）
- 遍历待排序数据，并且把数据一个一个放到对应的桶里去
- 对每个不是桶进行排序，可以使用其他排序方法，也递归排序
- 不是空的桶里数据拼接起来
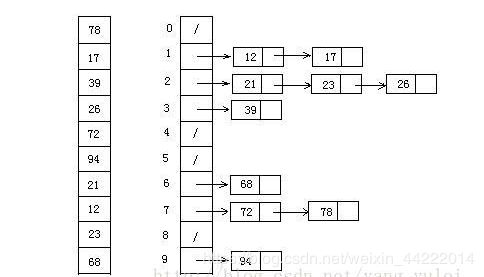
def bucket_sort(nums, bucketSize):
if len(nums) < 2:
return nums
_min = min(nums)
_max = max(nums)
# 需要桶个数
bucketNum = (_max - _min) // bucketSize + 1
buckets = [[] for _ in range(bucketNum)]
for num in nums:
# 放入相应的桶中
buckets[(num - _min) // bucketSize].append(num)
res = []
for bucket in buckets:
if not bucket: continue
if bucketSize == 1:
res.extend(bucket)
else:
# 当都装在一个桶里,说明桶容量大了
if bucketNum == 1:
bucketSize -= 1
res.extend(bucket_sort(bucket, bucketSize))
return res
算法分析：
稳定排序，外排序，时间复杂度O(n + k)，k为桶的个数。
10. 基数排序（Radix Sort）
基数排序是对数字每一位进行排序，从最低位开始排序
算法描述：
- 找到数组最大值，得最大位数；
- 从最低位开始取每个位组成radix数组；
- 对radix进行计数排序（计数排序适用于小范围的特点）。
def Radix_sort(nums):
if not nums: return []
_max = max(nums)
# 最大位数
maxDigit = len(str(_max))
bucketList = [[] for _ in range(10)]
# 从低位开始排序
div, mod = 1, 10
for i in range(maxDigit):
for num in nums:
bucketList[num % mod // div].append(num)
div *= 10
mod *= 10
idx = 0
for j in range(10):
for item in bucketList[j]:
nums[idx] = item
idx += 1
bucketList[j] = []
return nums
算法分析：
稳定排序，外排序，时间复杂度 posCount * (n + n)，其中 posCount 为数组中最大元素的最高位数；简化下得：O( k *n ) ；其中k为常数，n为元素个数。
三、算法总结
图片名词解释：
n: 数据规模
k: “桶”的个数
In-place: 占用常数内存，不占用额外内存
Out-place: 占用额外内存
码字不易，看过的同学麻烦点个赞~
关注或留言，看客官心情咯~
欢迎交流，共同进步~
您的支持，是我不断创作的最大动力~
欢迎点赞，关注，留言交流~
深度学习，乐此不疲~
个人微信公众号，欢迎关注~
