视觉SLAM总结——ORB SLAM2中关键知识点总结

视觉SLAM总结——ORB SLAM2中关键知识点总结

去年基于ORB SLAM2做了一些工作，当时把代码读了一遍但是没有进行总结，这几天抽时间复习了下ORB SLAM2，不打算从头到尾把代码分析一遍了（这种博客特别多，推荐参考ORB_SLAM2学习这个系列的博客，讲得很仔细，本文很大一部分是参考了这个博客），只是将中间一些比较关键的知识点进行一个总结，如下

1. ORB SLAM2的总体框架是怎样的？

下图是论文里的原图，ORB SLAM2一共有三个线程，分别是Tracking，Local Mapping和Loop Closing，其中Tracking是负责提取关键点进行帧间匹配，并且初选关键帧，Loop Mapping是进行关键帧筛选和地图点剔除，同事进行一个局部优化，Loop Closing主要是进行回环检测。

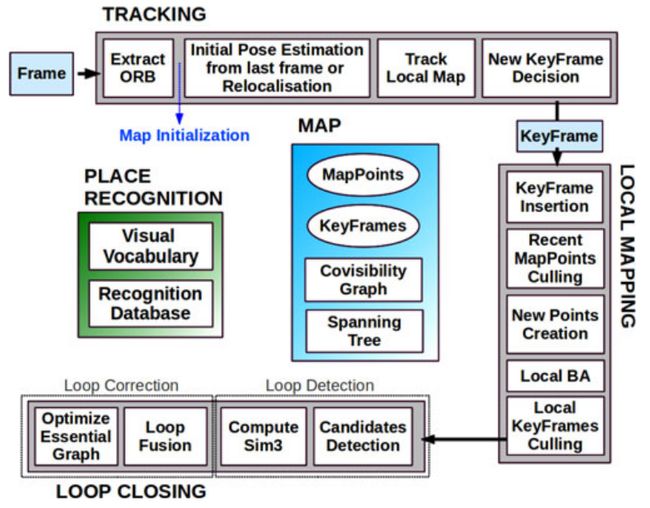
2. ORB SLAM2是怎样完成初始化的？

在ORB SLAM2进行跟踪前，需要先进行初始化，初始化包括相机初始帧位姿，新建地图，新建关键帧等，ORB SLAM2中一共提供了三种相机接口，其中单目初始化过程较为复杂，双目和RGBD初始化与其相似但较为简单，以单目为例，单目初始化过程如下：
（1）寻找匹配点，对前两帧图像提取ORB特征之后进行特征点匹配，若匹配个数少于100则匹配失败；
（2）由匹配点恢复位姿，利用八点法同时计算单应矩阵和基础矩阵，并通过计算评分比选择合适的结果作为初始位姿；
（3）创建初始地图，根据前两帧的位姿，利用三角法恢复三维地图点，创建初始地图，将这两帧都设为关键帧，并完成关键帧雨地图点，关键帧雨关键帧之间的关联，对上述两个关键帧和地图点进行一次全局BA，并选择地图点深度的中位数作为单位尺寸1来进行地图的尺寸初始化。

值得注意的是，单目初始化深度是通过三角化获得的，因此需要具有一定的平移，纯旋转不满足对极几何的要求因此无法进行三角化。

双目和RGBD初始化过程和单目不同的是，初始化过程不需要三角恢复深度，而是选取有深度的点进行初始化，因此只需要一个图像帧，而且没有创建关联和全局BA这些操作。

3. ORB SLAM2是如何进行Tracking的？

Tracking的目的是兼顾计算速度和鲁棒性使得当前帧中提取的特征点跟踪匹配到上一帧，在ORB SLAM2中一共使用了三种模型，分别是运动模型（TrackWithMotionModel）、关键帧模型（TrackReferenceKeyFrame）和重定位（Relocalization），其中
（1）运动模型：假定相机运动是匀速的，通过上一帧的速度和位姿估计下当前帧的位姿，然后进行跟踪匹配，这里要知道的是，如果帧和帧之间都采用暴力匹配的话运行速度会受到很大限制，因此作者是采用跟踪匹配加速了匹配过程（就是将上一帧的特征点投影到下一帧中，然后在投影点的附近区域进行搜索）；
（2）关键帧模型：就是和上一个关键帧进行匹配，这里是采用BoW进行匹配加速；
（3）重定位：和所有关键帧进行匹配，同样采用BoW进行匹配加速；
这几个模型的使用规则是，（1）不好使用（2），（2）不好使用（3），然后这里也可以看出，ORB SLAM2的作者为了提高程序运行速度无所不用其极。

在完成上述三个模型中的匹配后，程序还会将局部地图点投影到当前帧中实现一个匹配，目的是为了对局部地图和局部关键帧进行跟新（用作优化用，以提高精度）

4. ORB SLAM2是如何选取关键帧的？

关键帧的选取标准是：
（1）距离上一次重定位距离至少20帧；
（2）局部地图线程空闲，或者距离上一次加入关键帧过去了20帧,，如果需要关键帧插入（过了20帧）而Local Mapping线程忙，则发送信号给Local Mapping线程，停止局部地图优化，使得新的关键帧可以被及时处理；
（3）当前帧跟踪至少50个点，确保了跟踪定位的精确度；
（4）当前帧跟踪到Local Map中参考帧的地图点数量少于90%，确保关键帧之间有明显的视觉变化。
这里只是判断是否需要将当前帧创建为关键帧，并没有真的加入全局地图，因为Tracking线程的主要功能是局部定位，而处理地图中的关键帧、地图点，包括如何加入、如何删除的工作是在LocalMapping线程完成的。

5. ORB SLAM2中有那些（非线性/后端）优化相关的操作？

ORB SLAM2中一共有五种优化方式，分别是局部BA优化，全局BA优化，闭环位姿优化，全局位姿优化，单帧BA优化（这个名字是我自己取的，方便理解）
（1）局部BA优化：运行在Local Mapping线程中，在剔除关键帧之前进行局部地图优化，当新的关键帧加入到convisibility graph时，作者在关键帧附近进行一次局部优化，优化的目标是最小重投影误差。

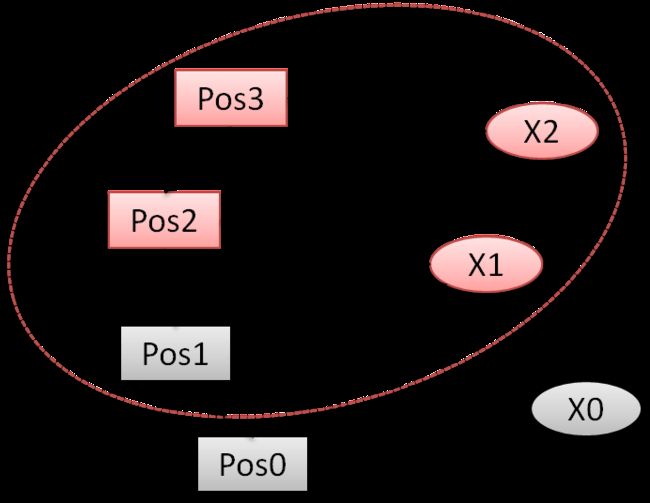
（2）全局BA优化：用于单目初始化的CreateInitialMapMonocular函数以及闭环优化的RunGlobalBundleAdjustment函数（在闭环结束前新开一个线程，进行全局优化。

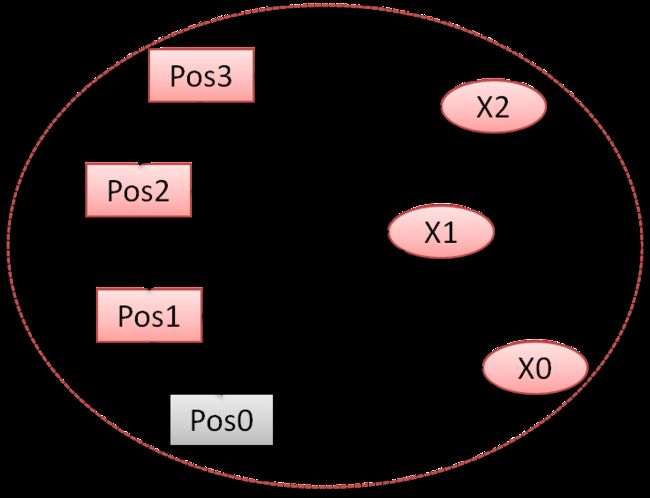
（3）闭环位姿优化：当检测到闭环时，闭环连接的两个关键帧的位姿需要通过Sim3/SE3优化（以使得其尺度一致）。优化求解两帧之间的相似变换矩阵，使得二维对应点（feature）的投影误差最小。

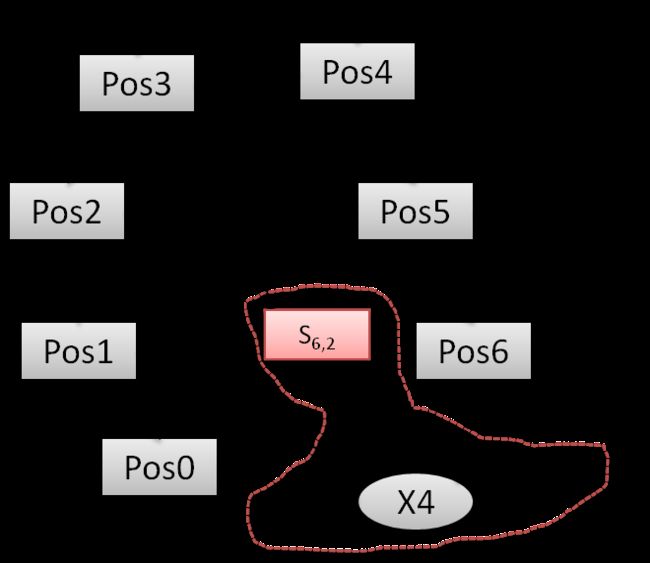
（4）全局位姿优化：这个优化就相当于《视觉SLAM十四讲》中的Pose Graph，值得注意的是如果是单目的话这里优化的是Sim3，如果是双目或者RGBD的话这里优化的SE3，残差定义为$e_{ij}=logSim3(S_{ij}{S}_{jw}{S}_{iw}^{-1})$，ORB SLAM2中优化的对象是Essential Graph，Essential Graph指的是所有的关键帧顶点，但是优化边大大减少，包括spanning tree（生成树）和共视权重$\theta >100$的边，以及闭环连接边，闭环调整CorrectLoop过程中的优化。

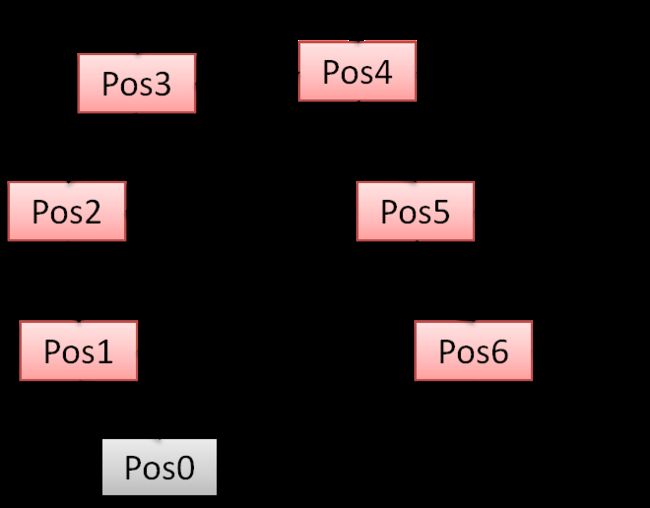
（5）单帧BA优化：只优化当前帧pose，地图点固定，用于LocalTracking中运动模型跟踪、参考帧跟踪、地图跟踪TrackLocalMap、重定位，每进行过一次PnP投影操作将地图点投影到当前平面上之后，都会进行一次PoseOptimization位姿优化，通过BA优化重投影误差

上面几张图(来自ORB_SLAM2学习之源码分析三-优化)把问题描述得非常清楚，红色的是优化的对象，灰色的是固定的对象，通过对比就能知道各个优化方法之间的区别。

6. ORB SLAM2中有维护了哪些图？

参考知乎问题，补充给出如下回答：
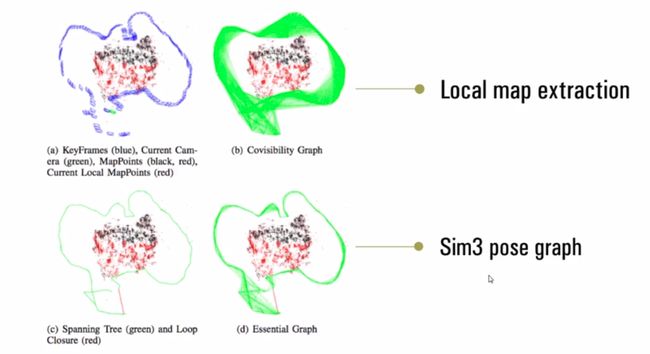
（1）Covisibility Graph：共视图，是一个无向有权图（Graph），这个概念最早来自2010的文章[Closing Loops Without Places]。该图中每个顶点就是关键帧，如果两个关键帧有相同的地图点（即它们有共视点），就把这两个顶点连接起来，连接边的权重就是两个关键帧共享的3D点的个数。局部BA优化依赖的就是一个局部的共视图，全局BA优化依赖的就是一个全局的共视图，总之共视图在ORB SLAM2中用得很多。
（2）Essential Graph：为了在优化阶段减小计算量，ORB-SLAM2作者提出了Essential Graph的概念，主要用它来进行全局位姿优化。它是共视图的子集，即Covisibity Graph的最小生成树（MST）。该图中顶点是关键帧，但只连接某个关键帧和与之拥有最多共享的地图点的关键帧，这样能够连接所有的顶点，但是边会减少很多。
（3）Spanning Graph：生成树，是代价最小的全联通图，Essential Graph就是基于Sanning Graph生成的。
如下图所示可以观察他们的区别：

7. ORB SLAM2中是如何对地图点进行筛选的？

在Local Mapping线程中在进行局部BA之前会先对地图点进行剔除，剔除规则如下：
（1）该地图点是坏点，直接从检查列表去掉；
（2）跟踪（匹配上）到该地图点的普通帧帧数（Increase Found）小于应该观测到该地图点的普通帧数量（25%*Increase Visible），即比值mnFound/mnVisible小于0.25，设置为坏点，并从检查列表去掉。比值低说明这样的地图点该地图点虽在视野范围内，但很少被普通帧检测到；
（3）从添加该地图点的关键帧算起，当前关键帧至少是第三个添加该地图点的关键帧的条件下，看到该地图点的帧数<=2（双目和RGBD模式是帧数<=3），设置为坏点，并从检查列表去掉；因此在地图点刚建立的阶段，要求比较严格，很容易被剔除；而且单目的要求更严格，需要三帧都看到；
（4）若从添加该地图点的关键帧算起，一共有了大于三个关键帧，还存在列表中，则说明该地图点是高质量的，从检查列表中去掉。

总而言之就是太少帧看到的地图点是坏点都要剔除掉，而看得多的则是高质量点

8. ORB SLAM2中是如何对关键帧进行剔除的？

候选的关键帧是LocalMapping中当前处理的关键帧的共视关键帧，不包括第一帧关键帧与当前关键帧。如果一个关键帧检测到的90%的地图点，在其他不少于三个具有相同或更精确尺度的关键帧里面都被检测到，就认定该关键帧冗余（该关键帧的存在提供的地图点观测信息有限），并剔除。

9. ORB SLAM2中Loop Closing的具体实现流程是怎样的？

首先是通过回环检测（Bow得分）和共视关系检查从所有关键帧中筛选出一组和当前帧有可能形成闭环的候选帧，然后利用相似求解器Sim3Solver求解出候选帧与当前帧之间的相似变换（注意这里是单目相似变换，而双目或者RGBD是刚体变换），利用相似变换找出更多的匹配地图点，然后进行闭环位姿优化（对应5中的回答），如果优化结果较好的话就不再判断其他候选帧。然后就是闭环矫正，通过就出来的相似变换对当前帧进行位姿调整并且传播到当前帧相连的关键帧，回环两侧的关键帧完成对齐，然后利用调整过的位姿更新这些相连关键帧对应的地图点，同时在Covisibility Graph里面增加闭环边，然后进行Essential Graph的优化（即全局位姿优化），当前帧与闭环匹配帧之间的边不进行优化，最后再来一个全局BA优化即完成了Loop Closing的全部流程。

10. 什么是Sim3优化？

注意Sim3优化是单目所特有的优化方式，因为单目具有尺度不确定性，对于空间点坐标$p$有如下相似变换：$$p^{\prime }=\left[\begin{array}{cc}s\mathbf{R}& \mathbf{t}\\ 0^T& 1\end{array}\right]\mathbf{p}=s\mathbf{R}\mathbf{p}+\mathbf{t}$$于是我们建立了一个相似变换群$Sim(3)$：$$\mathrm{Sim}(3)=\left\{\left[S=\begin{array}{ccc}S=& s\mathbf{R}& \mathbf{t}\\ 0^T& 1& \end{array}\right]\in {\mathbb{R}}^{4\times 4}\right\}$$其对应的李代数如下：$$\mathrm{sim}(3)=\left\{\zeta |\zeta =\left[\begin{array}{c}\rho \\ \varphi \\ \sigma \end{array}\right]\in {\mathbb{R}}^7,{\zeta }^{\wedge }=\left[\begin{array}{cc}\sigma I+{\varphi }^{\wedge }& \rho \\ 0^T& 0\end{array}\right]\in {\mathbb{R}}^{4\times 4}\right\}$$
其相较于欧式群的李代数其多了一个$\sigma$，变成了一个七维向量，而不是六维，关联 Sim(3) 和$\mathfrak{s}\mathfrak{i}\mathfrak{m}(3)$ 的仍是指数映射和对数映射。指数映射为$$\exp \left({\zeta }^{\wedge }\right)=\left[\begin{array}{cc}{e}^{\sigma }\exp \left({\varphi }^{\wedge }\right)& J_s\rho \\ 0^T& 1\end{array}\right]$$其中$$\begin{array}{rl}{\mathbf{J}}_s=& \frac{e^{\sigma }-1}{\sigma }\mathbf{I}+\frac{\sigma e^{\sigma }\sin \theta +\left(1-e^{\sigma }\cos \theta \right)\theta }{{\sigma }^2+{\theta }^2}{\mathbf{a}}^{\wedge }\\ & +\left(\frac{e^{\sigma }-1}{\sigma }-\frac{\left(e^{\sigma }\cos \theta -1\right)\sigma +\left(e^{\sigma }\sin \theta \right)\theta }{{\sigma }^2+{\theta }^2}\right){\mathbf{a}}^{\wedge }{\mathbf{a}}^{\wedge }\end{array}$$视觉SLAM总结——后端总结中总结的微分求导模型和扰动求导模型对其同样适用。Sim3优化其实就是Pose Graph优化，其优化目标残差是$$e_{i,j}=\log {\left(S_{ji}\ast S_{iw}\ast S_{jw}^{-1}\right)}_{\mathfrak{s}\mathfrak{i}\mathfrak{m}(3)}^{\vee }$$其优化效果如下：

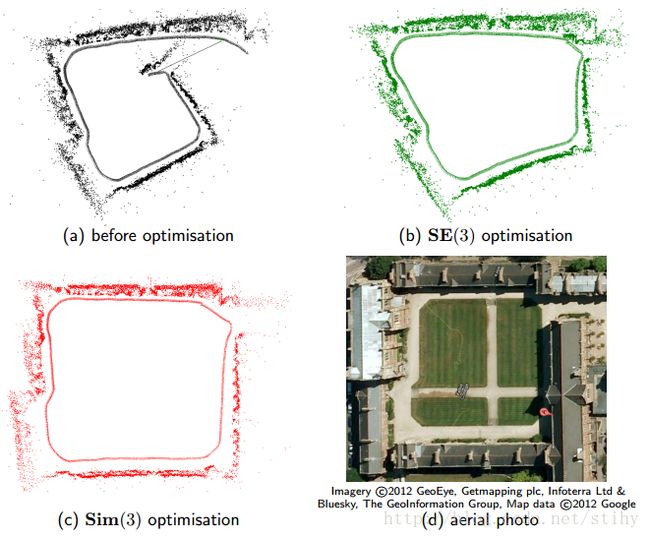
目前就先总结这么多知识点，我觉得题目可以改成《ORB SLAM2十问十答》，hhh，有问题欢迎交流～

补充：

11. ORB SLAM2中单目、双目和RGBD相机处理有哪些不同？

（1）在初始化的时候，这个地方很明显的，关于深度，单目是直接三角化，而双目和RGBD是直接用的深度图里面的深度
在Track()函数初始化阶段中有：

if(mState==NOT_INITIALIZED)//未进行初始化
{
   if(mSensor==System::STEREO || mSensor==System::RGBD)
       StereoInitialization();
   else
       MonocularInitialization();

   mpFrameDrawer->Update(this);

   if(mState!=OK)
       return;
}

MonocularInitialization()函数中里面涉及到的东西很多，其中包括分别计算F矩阵和H矩阵以及他们的得分，并确定用哪个矩阵恢复出来的变换关系进行三角化，代码太长就不贴出来了，在单目中深度的尺度是初始化时使得平均值为1确定的。
StereoInitialization();函数就相对较短了，最主要的部分是

 for(int i=0; i0)
     {
         cv::Mat x3D = mCurrentFrame.UnprojectStereo(i);//从相机坐标系转到世界坐标系
         MapPoint* pNewMP = new MapPoint(x3D,pKFini,mpMap);//往地图里添加的是世界坐标系下的关键点,每个关键点是一个类，这个点类知道自己对应的关键帧是哪个，地图是哪个
         pNewMP->AddObservation(pKFini,i);
         pKFini->AddMapPoint(pNewMP,i);
         pNewMP->ComputeDistinctiveDescriptors();//计算该点的描述子
         pNewMP->UpdateNormalAndDepth();//计算法向量和深度 TODO：法向量是干嘛的？
         mpMap->AddMapPoint(pNewMP);

         mCurrentFrame.mvpMapPoints[i]=pNewMP;
     }
 }

可以看到是判定关键点在深度图上是否有深度，有的话就直接用深度图的值生成空间点

cv::Mat Frame::UnprojectStereo(const int &i)
{
    const float z = mvDepth[i];
    if (z > 0)
    {
        const float u = mvKeysUn[i].pt.x;
        const float v = mvKeysUn[i].pt.y;
        const float x = (u - cx) * z * invfx;
        const float y = (v - cy) * z * invfy;
        cv::Mat x3Dc = (cv::Mat_(3, 1) << x, y, z);
        return mRwc * x3Dc + mOw;
    }
    else
        return cv::Mat();
}

（2）是在LocalMapping函数中生成新的地图点的时候，区别和上面第1点是一样的
代码如下

if(cosParallaxRays0 && (bStereo1 || bStereo2 || cosParallaxRays<0.9998))
{
    // Linear Triangulation Method
    cv::Mat A(4,4,CV_32F);
    A.row(0) = xn1.at(0)*Tcw1.row(2)-Tcw1.row(0);
    A.row(1) = xn1.at(1)*Tcw1.row(2)-Tcw1.row(1);
    A.row(2) = xn2.at(0)*Tcw2.row(2)-Tcw2.row(0);
    A.row(3) = xn2.at(1)*Tcw2.row(2)-Tcw2.row(1);

    cv::Mat w,u,vt;
    cv::SVD::compute(A,w,u,vt,cv::SVD::MODIFY_A| cv::SVD::FULL_UV);

    x3D = vt.row(3).t();

    if(x3D.at(3)==0)
        continue;

    // Euclidean coordinates
    x3D = x3D.rowRange(0,3)/x3D.at(3);

}
else if(bStereo1 && cosParallaxStereo1UnprojectStereo(idx1);                
}
else if(bStereo2 && cosParallaxStereo2UnprojectStereo(idx2);
}

这里面就是需要判定单目还是双目，新的空间点从双目中哪个去恢复更合适。

（3）最后就是在后端优化的时候，不管局部BA还是全局BA还是PnP，单目和双目(RGBD)的误差函数是不同的，双目和你说的一样需要将误差投到两个相机上，而且第二个相机上只有u这个方向上的误差
代码如下：

 if(pKF->mvuRight[mit->second]<0)
 {
     Eigen::Matrix obs;
     obs << kpUn.pt.x, kpUn.pt.y;

     g2o::EdgeSE3ProjectXYZ* e = new g2o::EdgeSE3ProjectXYZ();

     e->setVertex(0, dynamic_cast(optimizer.vertex(id)));
     e->setVertex(1, dynamic_cast(optimizer.vertex(pKF->mnId)));
     e->setMeasurement(obs);
     const float &invSigma2 = pKF->mvInvLevelSigma2[kpUn.octave];
     e->setInformation(Eigen::Matrix2d::Identity()*invSigma2);

     if(bRobust)
     {
         g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber;
         e->setRobustKernel(rk);
         rk->setDelta(thHuber2D);
     }

     e->fx = pKF->fx;
     e->fy = pKF->fy;
     e->cx = pKF->cx;
     e->cy = pKF->cy;

     optimizer.addEdge(e);
 }
 else
 {
     Eigen::Matrix obs;
     const float kp_ur = pKF->mvuRight[mit->second];
     obs << kpUn.pt.x, kpUn.pt.y, kp_ur;

     g2o::EdgeStereoSE3ProjectXYZ* e = new g2o::EdgeStereoSE3ProjectXYZ();

     e->setVertex(0, dynamic_cast(optimizer.vertex(id)));
     e->setVertex(1, dynamic_cast(optimizer.vertex(pKF->mnId)));
     e->setMeasurement(obs);
     const float &invSigma2 = pKF->mvInvLevelSigma2[kpUn.octave];
     Eigen::Matrix3d Info = Eigen::Matrix3d::Identity()*invSigma2;
     e->setInformation(Info);

     if(bRobust)
     {
         g2o::RobustKernelHuber* rk = new g2o::RobustKernelHuber;
         e->setRobustKernel(rk);
         rk->setDelta(thHuber3D);
     }

     e->fx = pKF->fx;
     e->fy = pKF->fy;
     e->cx = pKF->cx;
     e->cy = pKF->cy;
     e->bf = pKF->mbf;

     optimizer.addEdge(e);
 }

注意到单目定义的边是EdgeSE3ProjectXYZ()，双目定义的边是EdgeStereoSE3ProjectXYZ()，其中计算误差的函数是不同的，分别是

Vector2d EdgeSE3ProjectXYZ::cam_project(const Vector3d & trans_xyz) const{
  Vector2d proj = project2d(trans_xyz);
  Vector2d res;
  res[0] = proj[0]*fx + cx;
  res[1] = proj[1]*fy + cy;
  return res;
}

和

Vector3d EdgeStereoSE3ProjectXYZ::cam_project(const Vector3d & trans_xyz, const float &bf) const{
  const float invz = 1.0f/trans_xyz[2];
  Vector3d res;
  res[0] = trans_xyz[0]*invz*fx + cx;
  res[1] = trans_xyz[1]*invz*fy + cy;
  res[2] = res[0] - bf*invz;
  return res;
}

res[0]、res[1] 是$u_L、v_L$，res[2] 是$u_R=u_L-\frac{bf}{d}$。

$u_L、v_L,u_R$分别是什么呢？这就是一点比较有意思的事，RGBD相机在构造Frame的时候会构造成双目的相机模型，设置一个虚拟右图像，有个函数叫做ComputeStereoFromRGBD，就是完成这个功能的，如下：

void Frame::ComputeStereoFromRGBD(const cv::Mat &imDepth)
{
    mvuRight = vector(N, -1);
    mvDepth = vector(N, -1);

    for (int i = 0; i < N; i++)
    {
        const cv::KeyPoint &kp = mvKeys[i];
        const cv::KeyPoint &kpU = mvKeysUn[i];

        const float &v = kp.pt.y;
        const float &u = kp.pt.x;

        const float d = imDepth.at(v, u);

        if (d > 0)
        {
            mvDepth[i] = d;
            mvuRight[i] = kpU.pt.x - mbf / d;//把x坐标进行一定的修正，因为深度和彩色图不是同一个相机拍的
        }
    }
}

对应的就是视差公式$$u_R=u_L-\frac{bf}{d}$$另外，Frame传到后端确实没有了深度图，但是构造时已经记录了所有关键点的深度