数据结构与算法|第九章:排序-中
文章目录
- 数据结构与算法|第九章:排序-中
- 前言
- 1.项目环境
- 2.归并排序(Merge Sort)
- 2.1 原理图解
- 2.2 代码实现
- 2.3 排序分析
- 2.3.1 归并排序是原地排序算法吗?
- 2.3.2 归并排序是稳定排序算法吗?
- 2.3.3 时间复杂度
- 3.快速排序(Quick Sort)
- 3.1 原理图解
- 3.2 代码实现
- 3.2.1 分区方法1
- 3.2.2 分区方法2
- 3.3 排序分析
- 3.3.1 快速排序是原地排序算法吗?
- 3.3.2 插入排序是稳定排序算法吗?
- 3.3.3 时间复杂度
- 4.小结
- 5.参考
数据结构与算法|第九章:排序-中
前言
上一章我们讨论了冒泡排序(Bubble Sort)、插入排序(Insertion Sort)、选择排序(Selection Sort)三种排序算法,他们的平均时间复杂度都是 O ( n 2 ) O(n^2) O(n2),比较适合小规模数据量的排序。本章将会介绍两种时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn) 的排序算法,归并算法和快速排序,适合大数据量的排序,在实际开发中更为常用。
1.项目环境
- jdk 1.8
- github 地址:https://github.com/huajiexiewenfeng/data-structure-algorithm
- 本章模块:chapter07
2.归并排序(Merge Sort)
2.1 原理图解
排序一个数组,先将数组从中间分为两个数组,然后对两个部分再进行排序,最后将排序好的两部分合并在一起,这样整个数组都有序了。

归并算法采用的是分治的思想,分而治之,将一个大问题分解成一些小问题来处理,每个小问题都解决了,大问题自然而然就解决了。
分治算法一般都是用递归进行实现,我们利用 第七章:递归 的方法来进行分析
递推公式
merge_sort(p…r) = merge_sort( merge_sort(p…q) , merge_sort(q+1…r) )
终止条件
p>=r 不用再继续分解
merge_sort(p…r) 表示下标位置 p 到 r 之间的数组排序。
我们将这个问题分解成两个子问题,数组下标位置 [p…q] 以及 [q+1… r] 两个数组分别进行排序,数组下标 q 相当于数组的中间位置,也就是 (p+r)/2。
当两个数组排序完成之后,我们再将两个有序数组合并在一起。
2.2 代码实现
根据上面的分析我们使用 Java 代码进行实现
第一个过程是拆分的过程,将数组 numbers 拆分成 numbers1[0…q] 和 numbers2[q+1…r] 两个数组,使用递归的方式(为了理解方便,我们这里使用 numbers1 和 numbers2,实际可以不用这个两个数组进行存储)
private static int[] mergeSort(int[] numbers, int p, int r) {
if (p >= r) {
return new int[]{numbers[p]};
}
int q = (p + r) / 2;
int[] numbers1 = mergeSort(numbers, p, q);
int[] numbers2 = mergeSort(numbers, q + 1, r);
return mergeArray(numbers1, numbers2);
}
第二个过程是合并的过程
图解:
假设数组被拆成 numbers1[1,4] 和 numbers2[3,7,10] 两个数组,合并的过程大致如下
申请临时数组 tmpArray 大小为 数组1+数组2 的长度
数组1[0] 元素和 数组2[0] 比较,较小的元素 1 插入到临时数组 tmpArray[0] 个位置中
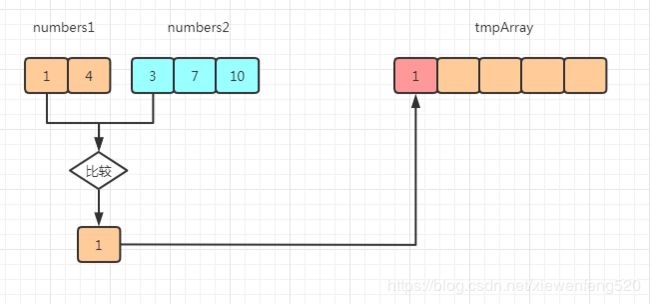
数组1[1] 元素和 数组2[0] 比较,较小的元素 3 插入到临时数组 tmpArray[1] 个位置中
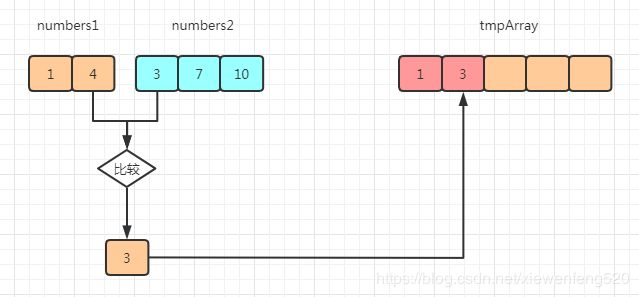
数组1[1] 元素和 数组2[1] 比较,较小的元素 4 插入到临时数组 tmpArray[2] 个位置中

数组2 剩余的元素 [7,10] 依次插入到 tmpArray[3,4] 中
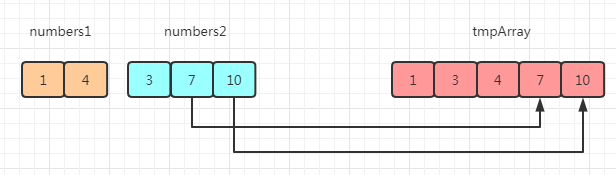
实现代码:
private static int[] mergeArray(int[] numbers1, int[] numbers2) {
int size1 = numbers1.length;
int size2 = numbers2.length;
// 申请临时数组
int[] tmpArray = new int[size1 + size2];
int i = 0;
int j = 0;
int k = 0;
// 数组1的元素依次和数组2的元素进行对比,将小元素放到临时数组中
while (i < size1 && j < size2) {
if (numbers1[i] <= numbers2[j]) {
tmpArray[k++] = numbers1[i++];
} else {
tmpArray[k++] = numbers2[j++];
}
}
// 查找数组1中剩余的没有比较的元素 移动到临时数组中
if (i < size1) {
int n = size1 - i;
for (int l = 0; l < n; l++) {
tmpArray[k++] = numbers1[i++];
}
}
// 查找数组2中剩余的没有比较的元素 移动到临时数组中
if (j < size2) {
int n = size2 - j;
for (int l = 0; l < n; l++) {
tmpArray[k++] = numbers2[j++];
}
}
// 将临时数组移动到原数组中
return tmpArray;
}
测试
public class MergeSortDemo {
public static void main(String[] args) {
int[] numbers = new int[]{7, 3, 10,1, 4, 2, 8, 6, 5};
testMergeSort(numbers);
}
private static void testMergeSort(int[] numbers) {
int size = numbers.length;
int p = 0;
int r = size - 1;
int[] res = mergeSort(numbers, p, r);
System.out.printf("排序结果为:%s\n", Arrays.toString(res));
}
...
}
执行结果:
排序结果为:[1, 2, 3, 4, 5, 6, 7, 8, 10]
2.3 排序分析
2.3.1 归并排序是原地排序算法吗?
不是,因为在递归和在合并的过程中,每次都需要开辟临时数组,所以空间复杂度并不是O(1),而是O(n)。
2.3.2 归并排序是稳定排序算法吗?
是的,是否稳定主要是看合并过程中,如果两个元素相等,是否前后交换了位置,而我们的实现代码中并没有,还是保证前后顺序的情况下,移动到临时数组中。
2.3.3 时间复杂度
因为涉及到递归,所以时间复杂度计算有点复杂
假设我们拆分数组 a 的时间是T(a),拆分数组 b、c的时间分别是T(b)、T©;合并数组 b、c 的时间为K,我们可以得到递归公式如下:
T ( a ) = T ( b ) + T ( c ) + K T(a) = T(b) + T(c) + K T(a)=T(b)+T(c)+K
是的计算递归的时间复杂度,也需要写递归公式。
假设对 n 个元素进行归并排序需要的时间是 T(n),那分解成两个子数组排序的时间都是 T(n/2)。从上面的代码可以看出,mergeArray() 函数合并两个有序子数组的时间复杂度是 O(n)。
所以,套用前面的公式,归并排序的时间复杂度的计算公式就是:
n=1 时, T ( 1 ) = C T(1) = C T(1)=C 只需要常量级的执行时间,所以表示为 C。
n >1 时, T ( n ) = 2 ∗ T ( n / 2 ) + n T(n) = 2*T(n/2) + n T(n)=2∗T(n/2)+n,
2 ∗ T ( n / 2 ) 2*T(n/2) 2∗T(n/2) 表示两个子数组的排序时间, n n n 表示 mergeArray() 的时间
通过这个公式,如何来求解 T(n) 呢?我们再进一步分解一下计算过程。
T ( n ) = 2 ∗ T ( n / 2 ) + n T(n) = 2*T(n/2) + n T(n)=2∗T(n/2)+n
= 2 ∗ ( 2 ∗ T ( n / 4 ) + n / 2 ) + n = 2*(2*T(n/4) + n/2) + n =2∗(2∗T(n/4)+n/2)+n
= 4 ∗ T ( n / 4 ) + 2 ∗ n = 4*T(n/4) + 2*n =4∗T(n/4)+2∗n
= 4 ∗ ( 2 ∗ T ( n / 8 ) + n / 4 ) + 2 ∗ n = 4*(2*T(n/8) + n/4) + 2*n =4∗(2∗T(n/8)+n/4)+2∗n
= 8 ∗ T ( n / 8 ) + 3 ∗ n = 8*T(n/8) + 3*n =8∗T(n/8)+3∗n
= 8 ∗ ( 2 ∗ T ( n / 16 ) + n / 8 ) + 3 ∗ n = 8*(2*T(n/16) + n/8) + 3*n =8∗(2∗T(n/16)+n/8)+3∗n
= 16 ∗ T ( n / 16 ) + 4 ∗ n = 16*T(n/16) + 4*n =16∗T(n/16)+4∗n
. . . . . . ...... ......
= 2 k ∗ T ( n / 2 k ) + k ∗ n = 2^k * T(n/2^k) + k * n =2k∗T(n/2k)+k∗n
通过这样一步一步分解推导,我们可以得到 T ( n ) = 2 k ∗ T ( n / 2 k ) + k ∗ n T(n) = 2^k*T(n/2^k)+k*n T(n)=2k∗T(n/2k)+k∗n。当 T ( n / 2 k ) = T ( 1 ) T(n/2^k)=T(1) T(n/2k)=T(1) 时,也就是 n / 2 k = 1 n/2^k=1 n/2k=1,我们得到 k = l o g 2 n k=log_2n k=log2n。我们将 k 值代入上面的公式,得到 T ( n ) = C ∗ n + n ∗ l o g 2 n T(n)=C*n+n*log_2n T(n)=C∗n+n∗log2n 。用大O标记法来表示 T ( n ) = O ( n l o g n ) T(n) =O(nlogn) T(n)=O(nlogn)。所以归并排序的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)。
最好时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),因为即使给的数组是完全有序的,我们还是需要进行拆分和合并的过程。
最坏时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),同样即使给的数组是倒序的,我们依然还是需要进行拆分和合并的过程。
平均时间复杂度: O ( n l o g n ) O(nlogn) O(nlogn),同理可得无论给的数组有序度是多少,都不会影响时间复杂度。
3.快速排序(Quick Sort)
3.1 原理图解
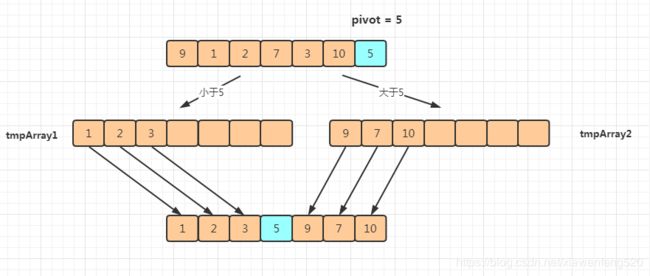
排序一个数组下标从 p 到 r 之间的元素,我们选择 p 到 r 之间的任意一个元素作为 pivot (分区点)。遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 放到右边,将 pivot 放到中间,经过这一步之后,数组被分为了三个部分。

假设 pivot (分区点) = 5,可以看到数组经过一次排序之后,[1,2,3,5,10] 这 5 个元素就在正确的位置上了。
递推公式
quick_sort(p…r) = quick_sort(p…q-1)+quick_sort(q+1…r)
终止条件
p>=r
3.2 代码实现
根据上面的分析,代码如下:
private static void quickSort(int[] numbers, int p, int r) {
if (p >= r) {
return;
}
int q = partition(numbers, p, r);// 获取分区点
quickSort(numbers, p, q - 1);
quickSort(numbers, q + 1, r);
}
分区的方法有两种,第一种比较好理解,空间复杂度较高;第二种实现的比较巧妙,需要反复理解体会
3.2.1 分区方法1
简单版本,比较浪费空间,不是原地排序
图解
申请两个临时数组 tmpArray1 和 tmpArray2
分区点取数组的最后一位,这里是元素 5
小于 5 放到 tmpArray1,大于 5 放到 tmpArray2
private static int partition(int[] numbers, int p, int r) {
int size = numbers.length;
int pivot = numbers[r];// 将数组的最后一个元素作为分区点
int[] tmpArray1 = new int[size];// 用来存储大于分区点的元素
int[] tmpArray2 = new int[size];// 用来存储小于分区点的元素
int j = 0;
int k = 0;
for (int i = p; i < r; i++) {
int number = numbers[i];
if (number <= pivot) {
tmpArray1[j++] = number;
} else {
tmpArray2[k++] = number;
}
}
// 将排序后的数组放回掉临时数组中
for (int i = 0; i < j; i++) {
numbers[p + i] = tmpArray1[i];
}
numbers[p + j] = pivot;
for (int i = 0; i < k; i++) {
numbers[p + i + j + 1] = tmpArray2[i];
}
return p + j;// 返回当前分区点所在的位置
}
3.2.2 分区方法2
升级版本,一般实际都是采用这一种,空间复杂度为 O(1)
定义两个下标,分别为 i 和 j,选择数组的最后一个元素作为 pivot 分区点,同样我们最后需要达到的效果是,小于 pivot 分区点的元素在数组的左边区间,大于 pivot 的元素在数组的右边区间,pivot 在数组的中间。
最开始 i = j = p,依次 数组[j] 元素与 pivot 进行比较,如果 数组[j] >pivot,不交换 数组[ i 和 j ] 位置,j ++,如果 数组[j] < pivot 交换 数组[ i 和 j ] 位置,i++,j++,最后当 j 等于 r 的时候,交换 数组[ i 和 j ] 位置,此时的 数组[j] 等于pivot ,将 pivot 放到了数组的中间。
图解
假设数组为 [9,1,2,7,3,10,5],5 为 pivot 分区点
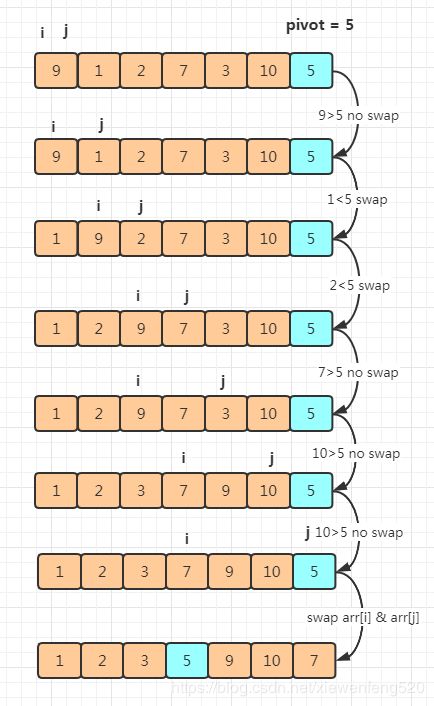
可以看到经过上面的步骤之后,[1,2,3] 都在 pivot 的左边,而 [9,10,7] 都在 pivot 的右边,但是这种方式不能保证排序算法的稳定性,因为7和9的位子前后放生了变化。
代码如下:
private static int partition(int[] numbers, int p, int r) {
int pivot = numbers[r];// 将数组的最后一个元素作为分区点
int i = p, j = p;
while (j < r) {
if(numbers[j] < pivot) {
swap(numbers, i, j);
i++;
}
j++;
}
swap(numbers, i, j);
return i;
}
private static void swap(int[] numbers, int i, int j) {
int tmp = numbers[i];
numbers[i] = numbers[j];
numbers[j] = tmp;
}
相对于 分区方法1 的实现优雅了很多,代码量更少,而且空间复杂度为O(1),属于原地排序。
3.3 排序分析
3.3.1 快速排序是原地排序算法吗?
都有可能,如果使用 分区方法1,明显不是原地排序,使用了大量的临时空间;但是升级版本的实现并没有使用额外的存储空间,所以它的空间复杂度是 O(1)。
3.3.2 插入排序是稳定排序算法吗?
都有可能,如果使用第一种分区是稳定排序,使用第二种相同元素位置可能发生交换,不是稳定排序。
3.3.3 时间复杂度
我们这里只考虑 分区方法2 的实现,因为在实际中都是使用这一种方式实现,目前代码还有一些需要优化的地方,我们后面的章节会做介绍。
如果每次分区操作,都能正好将数组分为大小接近的两个小区间,那么快排的时间复杂度求解公式和归并是相同的。所以快排的时间复杂度是 O ( n l o g n ) O(nlogn) O(nlogn)。
但是实际情况 pivot 很难每次都合适,假设我们的数组是完全有序的,每次以最后一个元素作为 pivot,那么每次分区都是不均匀的,我们要进行 n 次分区的操作,才能完成排序整个过程,每次分区我们都要扫描 n/2 个元素,这种情况时间复杂度就是 O ( n 2 ) O(n^2) O(n2) 。
上面两种情况分别代表了最好时间复杂度和最坏时间复杂度,那么平均时间复杂度是多少呢?
其实 T(n) 在大部分情况下的时间复杂度都可以做到 O ( n l o g n ) O(nlogn) O(nlogn),只有在极端情况下,才会退化到 O ( n 2 ) O(n^2) O(n2) 。而且,我们也有很多方法将这个概率降到很低,我们后面章节来进行讨论。
4.小结
| 排序算法 | 是否原地排序 | 是否稳定 | 时间复杂度 |
|---|---|---|---|
| 归并排序 | 否 | 是 | 最好: O ( n l o g n ) O(nlogn) O(nlogn) 最坏: O ( n l o g n ) O(nlogn) O(nlogn) 平均: O ( n l o g n ) O(nlogn) O(nlogn) |
| 快速排序 | 是 | 否 | 最好: O ( n l o g n ) O(nlogn) O(nlogn) 最坏: O ( n 2 ) O(n^2) O(n2) 平均: O ( n l o g n ) O(nlogn) O(nlogn) |
归并排序和快速排序是两种稍微复杂的排序算法,它们用的都是分治的思想,代码都通过递归来实现,过程非常相似。理解归并排序的重点是理解递推公式和 mergeArray() 合并函数。同理,理解快排的重点也是理解递推公式,还有 partition() 分区函数。
归并排序算法是一种在任何情况下时间复杂度都比较稳定的排序算法,这也使它存在致命的缺点,即归并排序不是原地排序算法,空间复杂度比较高,是O(n);正因为此,它也没有快排应用广泛。
快速排序算法虽然最坏情况下的时间复杂度是 O ( n 2 ) O(n^2) O(n2),但是平均情况下时间复杂度都是 O ( n l o g n ) O(nlogn) O(nlogn)。不仅如此,快速排序算法时间复杂度退化到 O ( n 2 ) O(n^2) O(n2) 的概率非常小,我们可以通过合理地选择 pivot 来避免这种情况。
5.参考
- 极客时间 -《数据结构与算法之美》王争