2020暑假牛客多校第一场（慢慢填坑，补的很慢...)

传送门
应该补的特别慢吧…
截至目前
F H J
I不算，最大流混过去了…等我学会带花树再补
------
F-Infinite String Comparision

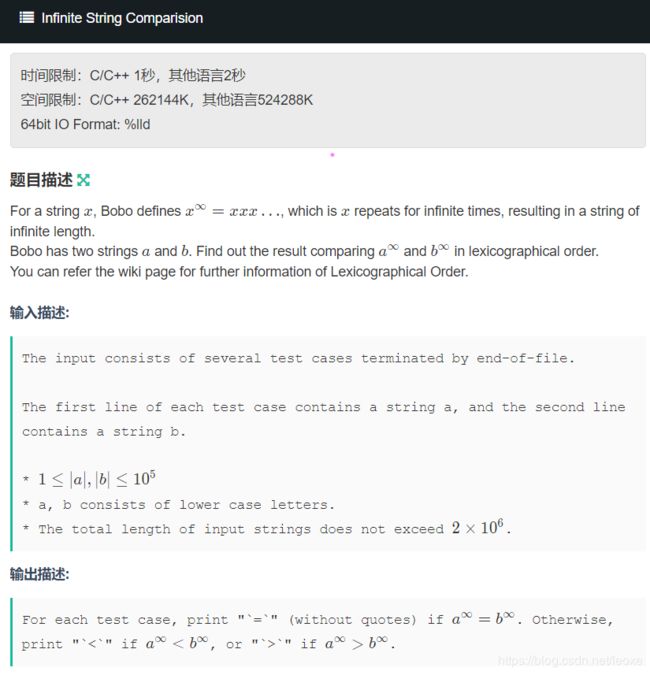
签到题，给出俩字符串，每个字符串都可以当循环节无限扩展，求出两者的字典序大小比较结果
这个没啥好说的，队友直接取最长的长度二倍就秒了，原理证明不太会，莽过去了

#include 
using namespace std;
string a, b;
int main () {
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    while(cin >> a >> b) {
        int res = 0;
        int len = 2 * max(a.size(), b.size());
        int lena = a.size(), lenb = b.size();
        for(int i = 0; i <= len; ++ i) {
            if(a[i % lena] > b[i % lenb]) {
                res = 1;
                break;
            } else if(a[i % lena] < b[i % lenb]) {
                res = -1;
                break;
            }
        }
        if(res == 0) {
            puts("=");
        } else if(res > 0) {
            puts(">");
        } else {
            puts("<");
        }
    }
    return 0;
}

H–Minimum-cost Flow

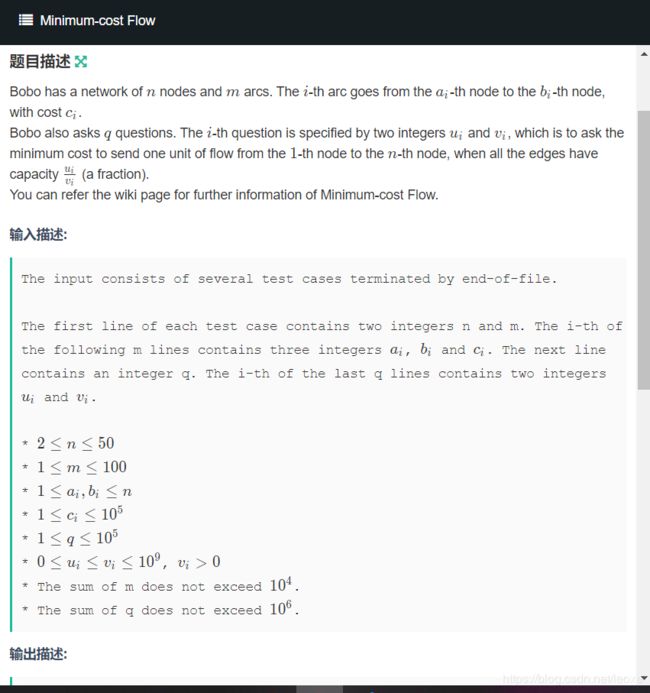
给出一个有向图和若干条边，以及每条边单位流量的费用（并没有给出容量），之后给出$q$个询问，每次询问给出$u$和$v$，假设每条边的容量均为$u/v$，求要获得$1$流量的最小费用是多少

每次询问都是$cap=u/v$,然后要求出$flow=1$的最小$cost$，这样很难处理，但是我们全体乘于$v$,转换成每次容量$cap=u$, 需要的流量$flow=v$, 的最小$cost$,最后$cost$除于$v$就可以了（很明显容量和流量，流量和花费是线性相关的…)
这个时候如果我们对于$q$次询问都建一次图，跑一次最小费用最大流的话显然是不现实的，这样会超时，我们可以在读入图的时候先跑一个最大流，后面直接根据比例求出答案，建图的时候把每条边都建成$cap=1$，然后跑一次最大流$maxflow$,假定为$x$

因为最初的时候$cap=1$,$maxflow=x$（$x$需要跑一次图求出来）
之后每一次要求的都是$cap=u$,$flow=v$,那么在$cap=u$的时候，我们能获得的最大流量就是$x\ast u$,比较这个值和$v$的关系那就可以知道是否可行了
在可行的基础上我们需要求出花费，由于容量是$u$,需要的流量为$v$,我们可以设$v=a\ast u+b$，也就是前$a$个$u$容量的加上一个$b$容量的花费
我们在求解最大流的过程中需要把每一次找到的费用储存起来，之后记录一个前缀和（每次找出的费用就是最低的，所以已经排好序了，同时每次的流量都是1），之后就把前$a$个的前缀和乘于$u$再加上第$a+1$次的费用乘于$b$就是答案了（注意特判是否整除来防止$a+1$越界（也就是b为0））
算出来的答案和$v$取个$gcd$然后化简分数就可以了
这题要开long long

struct Edge {
    int from, to, cap, flow, cost;
}edge[maxn];
struct MCMF {
    int n, m;
    vector<Edge> edges;
    vector<int> G[maxn];
    vector<int> sum, pre;
    bool inq[maxn];
    int dis[maxn], path[maxn], a[maxn];

    void init(int n) {
        this->n = n;
        pre.clear();
        sum.clear();
        for(int i = 0; i <= n; ++ i) {
            G[i].clear();
        }
        edges.clear();
    }

    void add_edge(int from, int to, int cap, int cost) {
        edges.push_back(Edge{from, to, cap, 0, cost});
        edges.push_back(Edge{to, from, 0, 0, -cost});
        m = edges.size();
        G[from].push_back(m - 2);
        G[to].push_back(m - 1);
    }

    bool bellman_ford(int s, int t, int& flow, int& cost) {
        for(int i = 0; i <= n; ++ i) dis[i] = inf;
        memset(inq, false, sizeof(inq));
        dis[s] = 0, inq[s] = true, path[s] = 0, a[s] = inf;
        queue<int> Q;
        Q.push(s);
        while(!Q.empty()) {
            int u = Q.front(); Q.pop();
            inq[u] = false;
            int sz = G[u].size();
            for(int i = 0; i < sz; ++ i) {
                Edge& e = edges[G[u][i]];
                if(e.cap > e.flow && dis[e.to] > dis[u] + e.cost) {
                    dis[e.to] = dis[u] + e.cost;
                    path[e.to] = G[u][i];
                    a[e.to] = min(a[u], e.cap - e.flow);
                    if(!inq[e.to]) {
                        Q.push(e.to);
                        inq[e.to] = true;
                    }
                }
            }
        }
        if(dis[t] == inf) {
            return false; // 求最小费用最大流
        }
        flow += a[t];
        cost += dis[t] * a[t];
        for(int u = t; u != s; u = edges[path[u]].from) {
            edges[path[u]].flow += a[t];
            edges[path[u] ^ 1].flow -= a[t];
        }
        return true;
    }

    int MinCostMaxFlow(int s, int t) {
        int flow = 0, cost = 0, dis = 0;
        while(bellman_ford(s, t, flow, cost)) {
            pre.push_back(cost);//前缀和
            dis = cost - dis;//这一次的费用
            sum.push_back(dis);//每一次流量为1的单独费用
            dis = cost;
        }
        return flow;
    }
}res;
void solve (int& kase) {
    int n, m, q;
    while(~scanf("%lld %lld", &n, &m)) {
        res.init(n);
        while(m --) {
            int u, v, w;
            scanf("%lld %lld %lld", &u, &v, &w);
            res.add_edge(u, v, 1, w);
        }
        int tot = res.MinCostMaxFlow(1,n);
        scanf("%lld", &q);
        while(q --) {
            int u, v;
            scanf("%lld %lld", &u, &v);
            if(tot * u >= v) {
                // v流量  u容量 v = u * a + b;
                // 前a个的u容量  第a + 1个的 b 容量
                int a = v / u, b = v % u;
                int ans = res.pre[a - 1] * u;
                if(b) {
                    ans += res.sum[a] * b;
                }
                int tmp = __gcd(ans, v);
                printf("%lld/%lld\n",ans / tmp, v / tmp);
            } else {
                puts("NaN");
            }
        }
    }
}

J–Easy Integration

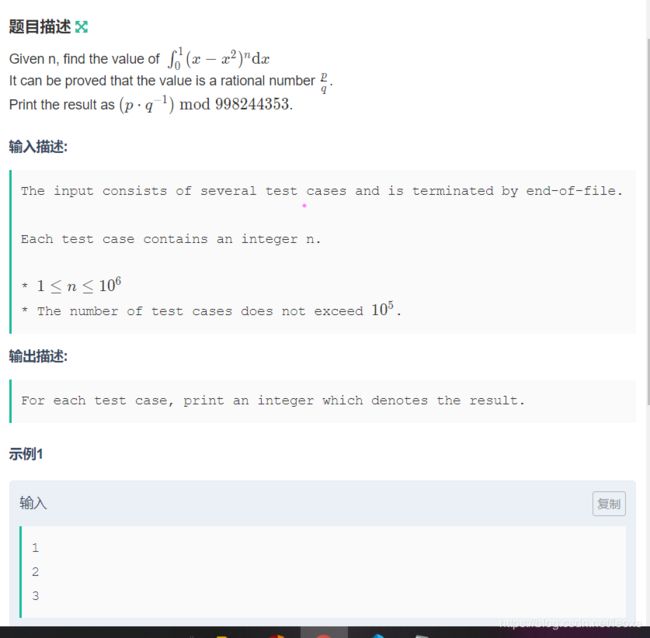
啊这个，就是求个积分，分部积分.，我肯定不会写
神仙队友带我躺了，丢了个公式出来就AC了
$$F(n)=F(n-1)\ast n^2/(2n(2n+1))$$
太神仙了…带我躺两场了
我是废物