二分图的最佳完美匹配——KM算法

二分图的最佳完美匹配

---

如果二分图的每条边都有一个权（可以是负数），要求一种完备匹配方案，使得所有匹配边的权和最大，记做最佳完美匹配。（特殊的，当所有边的权为1时，就是最大完备匹配问题）
我们使用KM算法解决该问题。

KM（Kuhn and Munkres）算法，是对匈牙利算法的一种贪心扩展，如果对匈牙利算法还不够明白，建议先重新回顾一下匈牙利算法。

KM是对匈牙利算法的一种贪心扩展，这种贪心不是对边的权值的贪心，算法发明者引入了一些新的概念，从而完成了这种扩展。

可行顶标

---

对于原图中的任意一个结点，给定一个函数 L(node) 求出结点的顶标值。我们用数组 lx(x) 记录集合 X 中的结点顶标值，用数组 ly(y) 记录集合 Y 中的结点顶标值。
并且，对于原图中任意一条边 edge(x,y) ,都满足

lx(x)+ly(y)>=weight(x,y)

相等子图

---

相等子图是原图的一个生成子图（生成子图即包含原图的所有结点，但是不包含所有的边）,并且该生成子图中只包含满足

lx(x)+ly(y)=weight(x,y)

的边,这样的边我们称之为 可行边。

算法原理

• 定理：如果原图的一个相等子图中包含完备匹配，那么这个匹配就是原图的最佳二分图匹配。

• 证明 ：由于算法中一直保持顶标的可行性，所以任意一个匹配的权值之和肯定小于等于所有结点的顶标之和，则相等子图中的完备匹配肯定是最优匹配。

这就是为什么我们要引入可行顶标和相等子图的概念。
上面的证明可能太过抽象，我们结合图示更直观的表述。

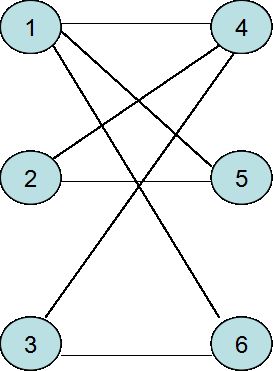
该图表示原图，且 X=1,2,3,Y=4,5,6 ,给出权值

weight(1,4)=5
weight(1,5)=10
weight(1,6)=15
weight(2,4)=5
weight(2,5)=10
weight(3,4)=10
weight(3,6)=20

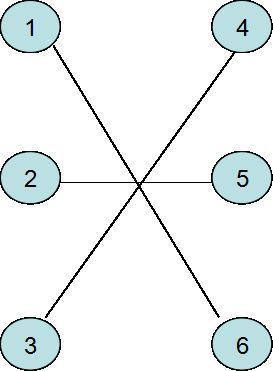
对于原图的任意一个匹配 M

那么对于

edge(1,6)weight(1,6)=15
edge(2,5)weight(2,5)=10
edge(3,4)weight(3,4)=10

都满足

lx(x)+ly(y)>=weight(x,y)

所以

∑i=1xi∈Xlx(xi)+∑i=1yi∈Yly(yi)=K>=∑weight(xi,yi)

可以看出，一个匹配中的边权之和最大为 K 。

那么很显然，当一个匹配 G∗ 的边权之和恰好为 K 时，那么 G∗ 就是二分图的最佳完美匹配。

如果对于每一条边 edge(xi,yi) 都满足

lx(xi)+ly(yi)==weight(xi,yi)

那么

∑i=1xi∈Xlx(xi)+∑i=1yi∈Yly(yi)=K=∑weight(xi,yi)

相等子图的完备匹配（完美匹配）即满足上述条件（因为相等子图的每条边都是可行边，可行边满足 lx(xi)+ly(yi)=weight(xi,yi) )所以当相等子图有完备匹配的时候，原图有最佳完美匹配。

KM的算法流程

---

流程

---

Kuhn－Munkras算法（即KM算法）流程：

1. 初始化可行顶标的值 (设定lx,ly的初始值)
2. 用匈牙利算法寻找相等子图的完备匹配
3. 若未找到增广路则修改可行顶标的值
4. 重复(2)(3)直到找到相等子图的完备匹配为止

KM算法的核心部分即控制修改可行顶标的策略使得最终可到达一个完美匹配。

1. 初始时，设定 lx[xi] 为和 xi 相关联的 edge(xi,yj) 的最大权值， ly[yj]=0 ,满足公式 lx[xi]+ly[yj]>=weight(xi,yj)
2. 当相等子图中不包含完备匹配的时候（也就是说还有增广路），就适当修改顶标。直到找到完备匹配为止。（整个过程在匈牙利算法中执行）

现在我们的问题是，遵循什么样的原则去修改顶标的值？

对于正在增广的增广路径上属于集合 X 的所有点减去一个常数 delta ，属于集合 Y 的所有点加上一个常数 delta 。

为什么要这样做呢，我们来分析一下：
对于图中任意一条边 edge(i,j) （其中 xi∈X，xj∈Y ）权值为 weight(i,j)

1. 如果i和j都属于增广路,那么 lx[i]−delta+ly[j]−+delta=lx[i]+ly[j] 值不变，也就说 edge(i,j) 可行性不变，原来是相等子图的边就还是，原来不是仍然不是
2. 如果i属于增广路，j不属于增广路,那么 lx[i]−delta+ly[j] 的值减小,也就是原来这条边不在相等子图中(否则j就会被遍历到了)，现在可能就会加入到相等子图。
3. 如果i不属于增广路，j属于增广路,那么 lx[i]+ly[j]+delta 的值增大，也就是说原来这条边不在相等子图中(否则j就会被遍历到了)，现在还不可能加入到相等子图
4. 如果i,j都不属于增广路，那么 lx[i ]和 ly[j] 都不会加减常数 delta 值不变,可行性不变

这 样，在进行了这一步修改操作后，图中原来的可行边仍可行，而原来不可行的边现在则可能变为可行边。那么delta的值应取多少？

观察上述四种情况，只有第二类边( xi∈X,yj∈Y )的可行性经过修改可以改变。

因为对于每条边都要满足 lx(i)+ly(j)>=weight(i,j) ，这一性质绝对不可以改变，所以取第二种情况的 lx[i]+ly[j]−weight(i,j) 的最小值作为 delta 。

证明 ：

delta=Min(lx[i]+ly[j]−weight(i,j))=lx[i]+ly[j]−Max(weight(i,j))

第二类边 :

lx[i]−delta+ly[j]=lx[i]−lx[i]−ly[i]+Max(weight(i,j))+ly[j]=Max(weight)>=weight(i,j)

成立

下面我们重新回顾一下整个KM算法的流程 ：

1. 可行顶标：每个点有一个标号，记( xi∈X,yj∈Y )。如果对于图中的任意边 edge(i,j) 都有 lx[i]+ly[j]>=weight(i,j) ，则这一顶标是可行的。特别地，对于lx[i]+ly[j]=weight(i,j)，称为可行边(也就是相等子图里的边）
2. KM 算法的核心思想就是通过修改某些点的标号（但要满足点标始终是可行的），不断增加图中的可行边总数，直到图中存在仅由可行边组成的完全匹配为止，此时这个 匹配一定是最佳的（证明上文已经给出）
3. 初始化： lx[i]=Max(edge(i,j)),xi∈X,edge(i,j)∈E ， ly[j]=0 。这个初始顶标显然是可行的，并且，与任意一个X方点关联的边中至少有一条可行边
4. 从每个 X 方点开始DFS增广。DFS增广的过程与最大匹配的Hungary算法基本相同，只是要注意两点：一是只找可行边，二是要把搜索过程中遍历到的 X 方点全部记下来，以便进行后面的修改
5. 增广的结果有两种：若成功（找到了增广路），则该点增广完成，进入下一个点的增广。若失败（没有找到增广路），则需要改变一些点的标号，使得图中可行边的 数量增加。
6. 修改后，继续对这个 X 方点DFS增广，若还失败则继续修改，直到成功为止

---

伪代码

bool findpath(x)
{
    visx[x] = true;
    for(int y = 1 ; y <= ny ; ++y)
    {
        if(!visy[y] && lx[x] + ly[y] == weight(x,y)) //y不在交错路中且edge(x,y)必须在相等子图中
        {
            visy[y] = true;
            if(match[y] == -1 || findpath(match[y]))//如果y还为匹配或者从y的match还能另外找到一条匹配边
            {
                match[y] = x;
                return true;
            }
        }
    }
    return false;
}
void KM()
{
    for(int x = 1 ; x <= nx ; ++x)
    {
        while(true)
        {
            memset(visx,false,sizeof(visx));//访问过X中的标记
            memset(visy,false,sizeof(visy));//访问过Y中的标记
            if(findpath(x))//找到了增广路，跳出继续寻找下一个
                break;
            else
            {
                for(int i = 1 ; i <= nx ; ++i)
                {
                    if(visx[i])//i在交错路中
                    {
                        for(int j = 1 ; j <= ny ; ++j)
                        {
                            if(visy[j])//j不在交错路中，对应第二类边
                                delta = Min(delta,lx[x] + ly[y] - weight(i,j))
                        }
                    }
                }
                for(int i = 1 ; i <= nx ; ++i)//增广路中xi - delta
                    if(visx[i])
                        lx[i] -= delta;
                for(int j = 1 ; j <= ny ; ++j)//增广路中yj + delta
                    if(visy[j])
                        ly[j] += delta;
            }

    }
}

这种形式的KM算法的时间复杂度为 O(n4)

---

KM算法的优化

KM算法可以优化到 O(n3)

一个优化是对 Y 顶点引入松弛函数 slack ， slack[j] 保存跟当前节点 j 相连的节点 i 的 lx[i]+ly[j]−weight(i,j) 的最小值，于是求 delta 时只需O(n)枚举不在交错树中的 Y 顶点的最小 slack 值即可。

松弛值可以在匈牙利算法检查相等子树边失败时进行更新，同时在修改标号后也要更新，具体参考代码实现。

(hdu 2255 模板)

/*
实际上，O(n^4)的KM算法表现不俗，使用O(n^3)并不会很大的提高KM的运行效率
需要在O(1)的时间找到任意一条边，使用邻接矩阵存储更为方便
*/
#include 
#include 
const int maxn = 305;
const int INF = 0x3f3f3f3f;
int match[maxn],lx[maxn],ly[maxn],slack[maxn];
int G[maxn][maxn];
bool visx[maxn],visy[maxn];
int n,nx,ny,ans;

bool findpath(int x)
{
    int tempDelta;

    visx[x] = true;
    for(int y = 0 ; y < ny ; ++y){
        if(visy[y]) continue;
        tempDelta = lx[x] + ly[y] - G[x][y];
        if(tempDelta ==  0){//(x,y)在相等子图中
            visy[y] = true;
            if(match[y] == -1 || findpath(match[y])){
                match[y] = x;
                return true;
            }
        }
        else if(slack[y] > tempDelta)
            slack[y] = tempDelta;//(x,y)不在相等子图中且y不在交错树中
    }
    return false;
}
void KM()
{

    for(int x = 0 ; x < nx ; ++x){
        for(int j = 0 ; j < ny ; ++j) slack[j] = INF;//这里不要忘了，每次换新的x结点都要初始化slack
        while(true){
            memset(visx,false,sizeof(visx));
            memset(visy,false,sizeof(visy));//这两个初始化必须放在这里,因此每次findpath()都要更新
            if(findpath(x)) break;
            else{
                int delta = INF;
                for(int j = 0 ; j < ny ; ++j)//因为dfs(x)失败了所以x一定在交错树中，y不在交错树中，第二类边
                    if(!visy[j] && delta > slack[j])
                        delta = slack[j];
                for(int i = 0 ; i < nx ; ++i)
                    if(visx[i]) lx[i] -= delta;
                for(int j = 0 ; j < ny ; ++j){
                    if(visy[j])
                        ly[j] += delta;
                    else
                        slack[j] -= delta;
                    //修改顶标后，要把所有的slack值都减去delta
                    //这是因为lx[i] 减小了delta
                    //slack[j] = min(lx[i] + ly[j] -w[i][j]) --j不属于交错树--也需要减少delta，第二类边
                }
            }
        }
    }
}
void solve()
{

   memset(match,-1,sizeof(match));
   memset(ly,0,sizeof(ly));
   for(int i = 0 ; i < nx ; ++i){
        lx[i] = -INF;
        for(int j = 0 ; j < ny ; ++j)
            if(lx[i] < G[i][j])
                lx[i] = G[i][j];
   }
   KM();
}
int main()
{
    while(scanf("%d",&n) != EOF){
        nx = ny = n;
        for(int i = 0 ; i < nx ; ++i)
            for(int j = 0 ; j < ny ; ++j)
                scanf("%d",&G[i][j]);
        solve();
        int ans = 0;
        for(int i = 0 ; i < ny ; ++i)
            if(match[i] != -1)
                ans += G[match[i]][i];
        printf("%d\n",ans);
    }
    return 0;
}

上面讲的都是求最大权的完备匹配，如果要求最小权完备匹配，只需在调用km算法前把所有权值都取反，然后再调用km算法，然后把km算法得到的结果再取反即为最小权值。

---

经典练习题目

poj 3565
hdu 2255
hdu 1533
hdu 1853
hdu 3488
hdu 3435
hdu 2426
hdu 2853
hdu 3718
hdu 3722
hdu 3395
hdu 2282
hdu 2813
hdu 2448
hdu 2236
hdu 3315
hdu 3523