（一）【机器人路径规划】路径规划概述

A 路径规划定义

移动机器人依据某个或某些性能指标（如工作代价最小、行走路线最短、行走时间最短等），在运动空间中找到一条从起始状态到目标状态、可以避开障碍物的最优或者接近最优的路径。
路径规划分为全局路径规划和局部路径规划

• 全局路径规划：是宏观的规划，主要为机器人在运动中提供核心运动点，保证机器人安全到达目的地，但全局路径规划生成的可能不是一条轨迹，而是一些离散的点。
• 局部路径规划：为了实现机器人的路线更加合理，还需要局部路径规划。它可以对机器人的速度、加速度等进行约束。

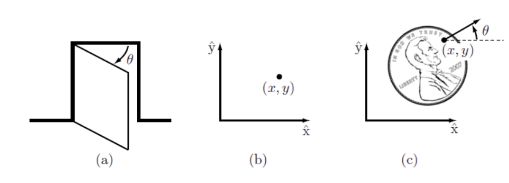
B 构型/位型空间（configuration Space）

构型/位型：能够反映机器人上每个点位置的变量

（a）中的$\theta$角就是门的构型
（b）中的点的坐标就是点的构型
（c）旋转角度$\theta$和坐标（x,y）构成硬币的构型。

机器人的自由度能反映构型。

构型/位型空间（C-space）：包含机器人所有构型的n维空间

---

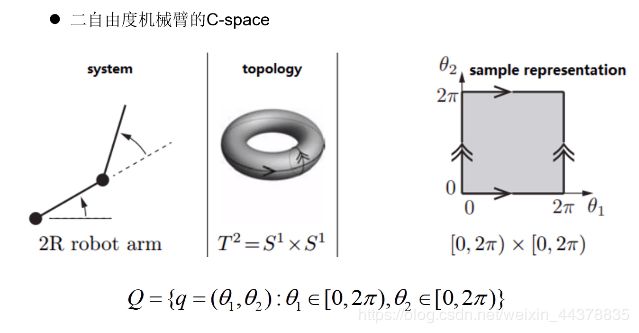
二自由度机械臂的两个关节角构成它的C-space，中间图为C-space的拓扑空间，最右为其坐标表示。

---

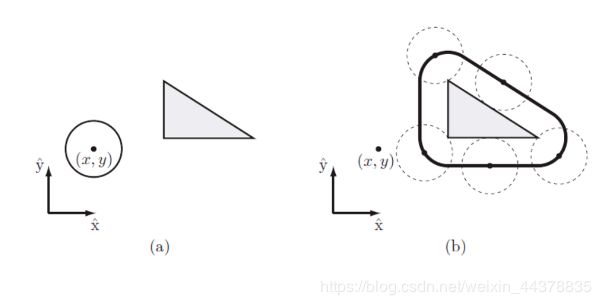
C 障碍物与构型空间

将构型空间障碍物$Q{O}_1$定义为机器人与工作空间中的障碍物$W{O}_1$相交的构型集合。

自由空间或自由构型空间$Q_{free}$是机器人不与任何障碍物相交的构型集合。

黄色为机器人；蓝色为障碍物。

---

例子：
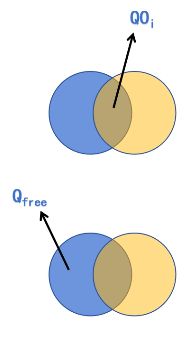
圆为机器人，三角形为障碍物

由于机器人本身是有工作半径的，把三角形机器人半径宽的外环都划分为障碍物部分。则自由此例子的自由构型空间就是实际障碍物部分。

---

C 环境模型建立

定义：建立机器人所处环境中的各种物体，包括障碍、路标等的准确空间位置描述，即建立空间模型或地图。

两种建立环境模型方法：
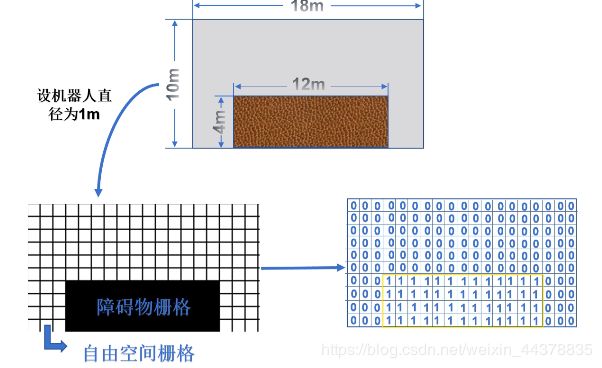
<1>栅格法
所谓栅格法，是将移动机器人需要工作的环境信息分割成等大小的正方形栅格，此方法是W.E.Howden提出的，并成为移动机器人路径规划最常用的地图建模方法。
如：

---

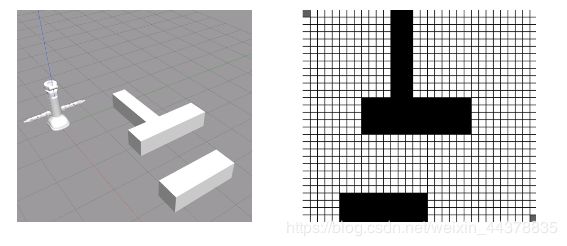
栅格法环境信息表示方法：
障碍物栅格赋值为1，自由空间栅格赋值为0。

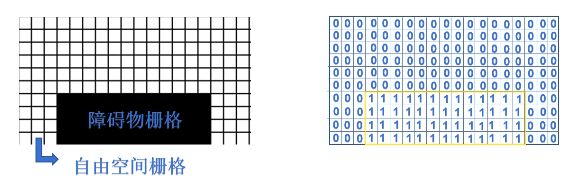
重要参数：栅格大小：
栅格法建模，栅格大小的选取尤为重要，既要考虑机器人尺寸，也要考虑到整个环境的复杂程度。

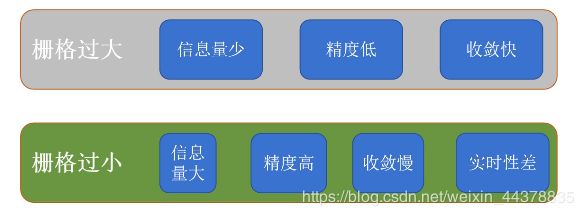
较为理想的栅格单位长度为机器人的直径大小。

---

栅格法环境信息表示方法：

---

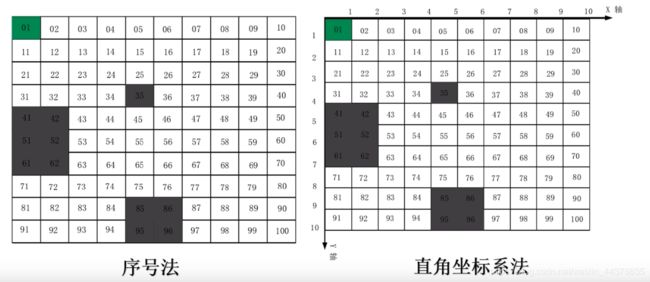
栅格地图的标识方法：
栅格地图建立模型后，需要将整个二维工作区内的栅格单元用序号法或直角坐标系法进行标识。这样有助于移动机器人对栅格单元位置的记录，分辨出是障碍物栅格还是可以通过的自由空间栅格。

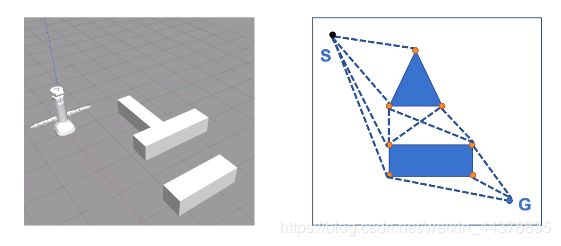
<2>可视图法

所谓可视图，是在二维情况下，起点S、障碍物的顶点以及目标点G相连，并确保所有直线段不穿过障碍物，得到的图称之为可视图。

---

D 欧氏距离与曼哈顿距离

<1>欧氏距离
在二维和三维空间中的欧氏距离的计算公式分别为：

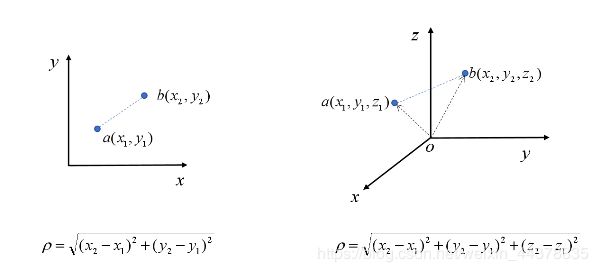
两个n维向量$a(x_{11},x_{21}，...,x_{1n})$与$b(x_{21},x_{22},...,x_{2n})$间的欧式距离为：
$${\rho }_{12}=\sqrt{\sum _{k=1}^n(x_{1k}-x_{2k}{)}^2}$$

<2>曼哈顿距离
顾名思义，在曼哈顿街区，要从一个十字路口到另一个十字路口，驾驶距离显然不是两点间的直线距离，这个实际驾驶距离就是曼哈顿距离，它也称为城市街区距离。

---