数据结构 | TencentOS-tiny中队列、环形队列、优先级队列的实现及使用
1. 什么是队列
队列（queue）是一种只能在一端插入元素、在另一端删除元素的数据结构，遵循先入先出（FIFO）的规则。
队列中有两个基本概念：
- 队头指针（可变）：永远指向此队列的第一个数据元素；
- 队尾指针（可变）：永远指向此队列的最后一个数据元素；
队列中的数据存储方式有两种：
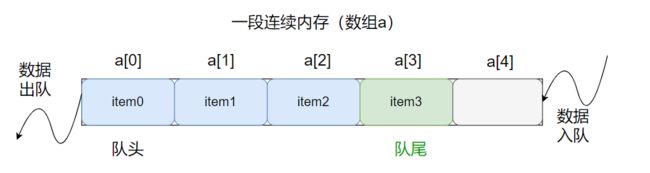
① 基于静态连续内存（数组）存储，如图：
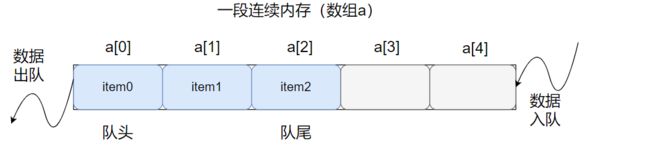
② 基于动态内存（链表节点）存储，如图：
后续都使用基于静态内存存储的队列讲解。
队列提供两个统一的操作：
- 入队（enqueue）
入队将一个元素添加到队尾，并将队尾指针+1后移，如图：
- 出队（dequeue）
出队将从队头中取出一个元素，并将队头指针+1后移，如图：
2. 环形队列
2.1. 环形队列的特点
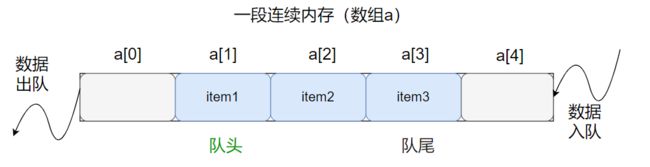
普通队列的入队操作将队尾指针后移+1，出队操作将队头指针后移+1，操作几次之后会发现队头指针和队尾指针都跑到缓冲区的尾部去了：
这就导致了前面的内存空间全被浪费，如果要重新恢复使用，则需要进行元素和指针的移动：
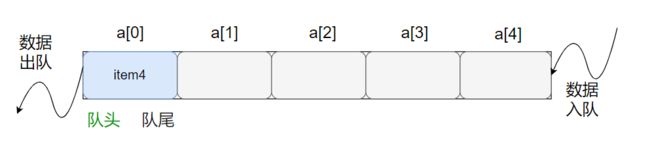
显然这种队列使用方式太不方便了，所以就诞生了环形队列：不用搬移元素和指针，一直可以重复利用这段内存空间。
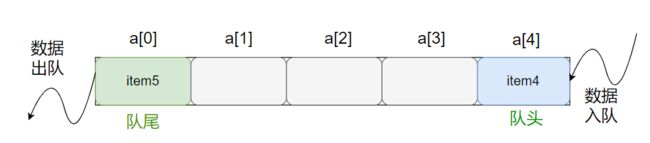
2.2. 环形队列的实现
TencentOS-tiny中环形队列的实现在tos_ring_queue.h和tos_ring_queue.c中。
typedef struct k_ring_queue_st {
knl_obj_t knl_obj;
uint16_t head; //队头指针
uint16_t tail; //队尾指针
size_t total; //记录队列中元素的个数
uint8_t *pool; //队列底层的存储结构（一个数组）
size_t item_size; //队列中每个元素的大小，单位：字节
size_t item_cnt; //队列中可以容纳的元素数量
} k_ring_q_t;
环形队列初始化，将队头指针和队尾置0：
__API__ k_err_t tos_ring_q_create(k_ring_q_t *ring_q, void *pool, size_t item_cnt, size_t item_size)
{
//省略了参数合法性检查代码
ring_q->head = 0u;
ring_q->tail = 0u;
ring_q->total = 0;
ring_q->pool = (uint8_t *)pool;
ring_q->item_size = item_size;
ring_q->item_cnt = item_cnt;
return K_ERR_NONE;
}
判断环形队列是否为满或者为空：
__API__ int tos_ring_q_is_empty(k_ring_q_t *ring_q)
{
TOS_CPU_CPSR_ALLOC();
int is_empty = K_FALSE;
//省略了参数合法性检查代码
TOS_CPU_INT_DISABLE();
is_empty = (ring_q->total == 0 ? K_TRUE : K_FALSE);
TOS_CPU_INT_ENABLE();
return is_empty;
}
__API__ int tos_ring_q_is_full(k_ring_q_t *ring_q)
{
TOS_CPU_CPSR_ALLOC();
int is_full = K_FALSE;
//省略了参数合法性检查代码
TOS_CPU_INT_DISABLE();
is_full = (ring_q->total == ring_q->item_cnt ? K_TRUE : K_FALSE);
TOS_CPU_INT_ENABLE();
return is_full;
}
环形队列入队操作的API如下：
__API__ k_err_t tos_ring_q_enqueue(k_ring_q_t *ring_q, void *item, size_t item_size);
在此API中，入队操作的实现如下：
__STATIC_INLINE__ void ring_q_item_increase(k_ring_q_t *ring_q)
{
ring_q->tail = RING_NEXT(ring_q, ring_q->tail);
++ring_q->total;
}
环形队列出队操作的API如下：
__API__ k_err_t tos_ring_q_dequeue(k_ring_q_t *ring_q, void *item, size_t *item_size);
在此API中，出队操作的实现如下：
__STATIC_INLINE__ void ring_q_item_decrease(k_ring_q_t *ring_q)
{
ring_q->head = RING_NEXT(ring_q, ring_q->head);
--ring_q->total;
}
在入队和出队操作的时候都使用了 RING_NEXT 宏，用来获取在环形队列中的下一个位置：
#define RING_NEXT(ring_q, index) ((index + 1) % ring_q->item_cnt)
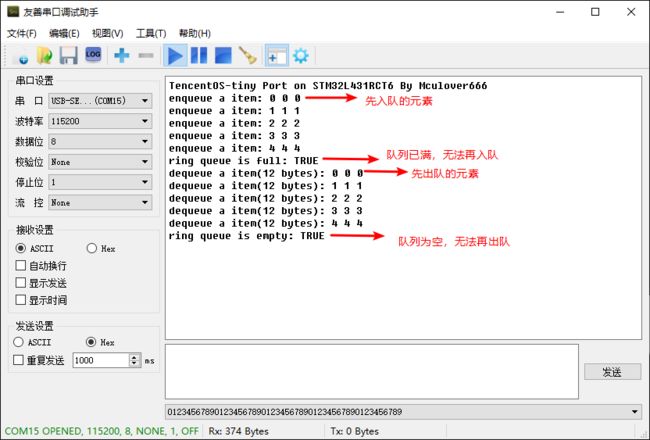
2.3. 环形队列使用Demo
编写如下的测试代码：
#include 运行结果如下：
3. 优先级队列
3.1. 优先级队列的特点
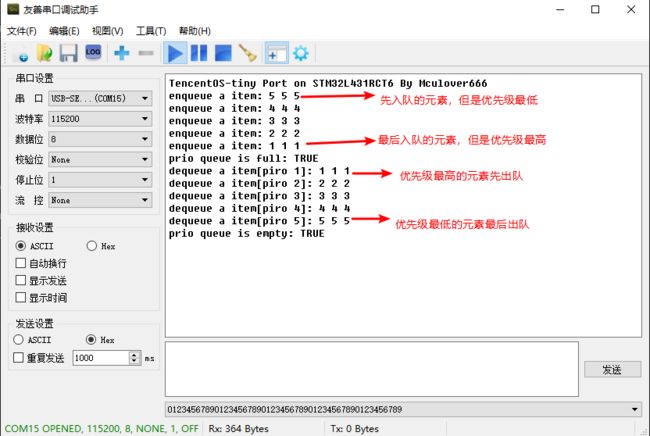
优先级队列也是一种基于队列的数据结构，但是它不遵循FIFO，而是按照每个元素的优先级进行出队：最高优先级的先出队。
3.2. 优先级队列的实现
TencentOS-tiny中环形队列的实现在tos_prio_queue.h和tos_prio_queue.c中。
优先级队列在数据入队的时候，会按照入队元素的优先级进行一次排序，将优先级值最小（优先级最高的元素）放在队头，出队的时候只需要取第一个元素即可。
正是因为这种特性，优先级队列的底层存储结构不能使用数组（排序太麻烦），而是使用了二项堆的数据结构。
二项堆是一种二叉树集合的数据结构，在本文中不再深入讲解，有兴趣的读者可以自己搜索阅读。
下面只给出优先级队列的API，理解其规则，会用即可。
- 创建优先级队列
__API__ k_err_t tos_prio_q_create(k_prio_q_t *prio_q, void *mgr_array, void *pool, size_t item_cnt, size_t item_size);
| 参数 | 描述 |
|---|---|
| prio_q | 优先级队列控制块指针 |
| mgr_array | 提供一块缓冲区用于内部管理 |
| pool | 队列的缓冲区 |
| item_cnt | 队列可容纳的元素数量 |
| item_size | 每个元素的大小，单位字节 |
其中用于内部管理的缓存区大小可以使用宏定义来计算，比如有5个元素的管理缓冲区大小：
uint8_t mgr_pool[TOS_PRIO_Q_MGR_ARRAY_SIZE(5)];
- 元素入队
__API__ k_err_t tos_prio_q_enqueue(k_prio_q_t *prio_q, void *item, size_t item_size, k_prio_t prio);
其中优先级的值遵循：数值越小，优先级越高。
- 元素出队
__API__ k_err_t tos_prio_q_dequeue(k_prio_q_t *prio_q, void *item, size_t *item_size, k_prio_t *prio);
其中prio需要传入一个地址，用于记录出队元素的优先级。
3.3. 优先级队列使用Demo
#include 运行结果为：
4. 总结
① 普通队列是一种只能在一端入队，在一端出队的数据结构，规则：FIFO。
② 环形队列对内存空间的利用率最高，使用最多，规则：FIFO。
③ 优先级队列不遵循FIFO，每个元素都有自己的优先级，规则：优先级最高的元素先出队。
接收更多精彩文章及资源推送，欢迎订阅我的微信公众号：『mculover666』。
