「BZOJ4651」「NOI2016」 网格
题目描述
跳蚤国王和蛐蛐国王在玩一个游戏。
他们在一个 n n 行 m m 列的网格上排兵布阵。其中的 c c 个格子中 (0≤c≤nm) ( 0 ≤ c ≤ n m ) ,每个格子有一只蛐蛐,其余的格子中,每个格子有一只跳蚤。
我们称占据的格子有公共边的两只跳蚤是相邻的。
我们称两只跳蚤是连通的,当且仅当这两只跳蚤相邻,或存在另一只跳蚤与这两只跳蚤都连通。
现在,蛐蛐国王希望,将某些(零个,一个或多个)跳蚤替换成蛐蛐,使得在此之后存在至少两只跳蚤不连通。
例如:我们用图 表示一只跳蚤,用图
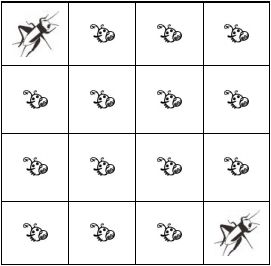
表示一只跳蚤,用图![]() 表示一只蛐蛐,那么左图描述了一个 n=4, m=4, c=2 n = 4 , m = 4 , c = 2 的情况。
表示一只蛐蛐,那么左图描述了一个 n=4, m=4, c=2 n = 4 , m = 4 , c = 2 的情况。
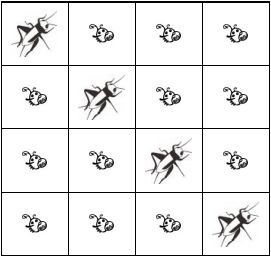
这种情况下蛐蛐国王可以通过将第二行第二列,和第三行第三列的两只跳蚤替换为蛐蛐,从而达成他的希望,如右图所示。并且,不存在更优的方案,但是可能存在其他替换两只跳蚤的方案。
你需要首先判断蛐蛐国王的希望能否被达成。如果能够达成,你还需要最小化被替换的跳蚤的个数。
输入格式
每个输入文件包含多组数据。
输入文件的第一行只有一个整数 T T ,表示数据的组数。
接下来依次输入 T T 组数据,每组数据的第一行包含三个整数 n,m,c n , m , c 。
接下来 c c 行,每行包含两个整数 x,y x , y 表示第 x x 行,第 y y 列的格子被一个蛐蛐占据。每一组数据当中,同一个蛐蛐不会被多次描述。
同一行相邻的整数之间由一个空格隔开。
输出格式
对于每一组数据依次输出一行答案。
如果这组数据中,蛐蛐国王的希望不能被达成,输出-1。否则,输出被替换的跳蚤的个数的最小值。
样例
样例输入
4
4 4 2
1 1
4 4
2 3 1
1 2
2 2 2
1 1
2 2
1 1 0样例输出
2
1
0
-1样例解释
第一组数据就是问题描述中的例子。
对于第二组数据,可以将第二行第二列的一只跳蚤替换为蛐蛐,从而使得存在两只跳蚤不连通,并且不存在更优的方案。
对于第三组数据,最初已经存在两只跳蚤不连通,故不需要再进行替换。
对于第四组数据,由于最多只有一只跳蚤,所以无论如何替换都不能存在两只跳蚤不连通。
数据范围与提示
对于所有的数据, 1≤n,m≤109, 0≤c≤min(nm,105), 1≤x≤n, 1≤y≤m, 1≤T≤20 1 ≤ n , m ≤ 10 9 , 0 ≤ c ≤ min ( n m , 10 5 ) , 1 ≤ x ≤ n , 1 ≤ y ≤ m , 1 ≤ T ≤ 20 。
我们记 ∑c ∑ c 为某个测试点中,其 T T 组输入数据的所有 c c 的总和,则保证 ∑c≤105 ∑ c ≤ 10 5 。
题解
首先答案不会超过 2 2 ,因为至少有一个跳蚤所在的格子相邻的跳蚤不超过 2 2 个。
对于答案是 −1 − 1 的情况,有两种情况:
1. 只有一只跳蚤。
2. 只有两只跳蚤,并且他们相邻。
图不连通的时候答案为 0 0 。 图有割点的情况答案为 1 1 (把割点便乘蛐蛐)。其他的情况答案就是 2 2 。
然后转化成了一张网格图让你求割点。
考虑到蛐蛐数量很少,连续 >2 > 2 行跳蚤与 2 2 行跳蚤是等价的,所以可以直接离散化,于是就能得到 84 84 分了。
但是蛐蛐有 105 10 5 次方级别,很显然不能直接离散化。
std 的思路非常妙,就是只保留每个蛐蛐周围 5×5 5 × 5 共 25 25 个格子,中间空出来的直接连边。于是点数是 2.5×106 2.5 × 10 6 级别的,可以通过,复杂度 O(c) O ( c ) 。
My Code
#include