六自由度焊接机器人——基于matlab robotics toolbox求解工作空间(蒙特卡洛算法)及绕定点转动的轨迹规划

1 6自由度焊接机器人DH模型

该六自由度机械臂能够实现操作器尖端的灵巧工作空间非空且含有内点，并能够规划机械臂各关节的轨迹，使操作器绕灵巧工作空间的某个内点作定点转动，即操作器尖端位置不变，操作器姿态变化，进一步地，可以实现工业焊接功能。
该6自由度焊接机器人使用 standard D-H（SDH）法建立坐标系，建立运动学模
型。最终形成的连杆模型和坐标系如下图：

得到标准 D-H 参数如下表：

2 基于matlab robotics toolbox的蒙特卡洛算法求解工作空间

基于上面的6自由度焊接机器人的DH模型，利用matlab robotics toolbox建立机器人的连杆模型。如下：

利用蒙特卡洛算法求解机械臂可行的工作空间，实验代码如下：

clear;
clc;
% %建立机器人模型
%        theta    d        a        alpha     offset
L1=Link([pi/2     85       27       -pi/2     0     ]); %定义连杆的D-H参数
L2=Link([-pi/2    0        102      0         0     ]);
L3=Link([0        0        20       -pi/2     0     ]);
L4=Link([0        96       0         pi/2     0     ]);
L5=Link([0        0        0        -pi/2     0     ]);
L6=Link([0        39       0        0         0     ]);
robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','manji'); %连接连杆，机器人取名manji
%% 为每一个关节设置旋转角度限制
l1u = 180.0;
l1d = -180.0;
l2u = -90.0;
l2d = 90.0;
l3u = -90.0;
l3d = 90.0;
l4u = -180.0;
l4d = 180.0;
l5u = -90.0;
l5d = 90.0;
l6u = -180.0;
l6d = 180.0;
%% 示教并进行工作空间计算
teach(robot); 
robot.plot([pi/2,-pi/2,0,0,0,0])
hold on;
N=2000; %随机取得的工作点个数

theta1=(l1d+(l1u-l1d)*rand(N,1))*pi/180; %随机取得关节1角度
theta2=(l2d+(l2u-l2d)*rand(N,1))*pi/180; %随机取得关节2角度
theta3=(l3d+(l3u-l3d)*rand(N,1))*pi/180; %随机取得关节3角度
theta4=(l4d+(l4u-l4d)*rand(N,1))*pi/180; %随机取得关节4角度
theta5=(l5d+(l5u-l5d)*rand(N,1))*pi/180; %随机取得关节5角度
theta6=(l6d+(l6u-l6d)*rand(N,1))*pi/180; %随机取得关节6角度

for n=1:1:N
q=[theta1(n),theta2(n),theta3(n),theta4(n),theta5(n),theta6(n)];
robot.plot(q);%动画显示
p=robot.fkine(q);
a=zeros(3,1);
a(:,1)=p(1,1,1).t;
plot3(a(1,1),a(2,1),a(3,1),'b.','MarkerSize',0.5);%画出落点
hold on;
end

得到该六自由度焊接机械臂的可行工作空间如下图（用蓝色点表示末端执行器的末端位置）：

可以发现该6自由度机械臂基本能满足机械臂的工作空间在一定空间内完整且灵巧的设计要求 。

3 绕定点转动的轨迹规划

在matlab robotics toolbox中，可以利用轨迹规划函数jtraj()进行五次插值多项式插值，得到角度、角速度和角加速度变化连续的轨迹。
对于一般的轨迹规划，我们可以直接用上面的方法，jtraj()函数插值得到。
对于绕定点转动的轨迹规划，最基本的要求就是末端点在姿态变化时，末端点位置不变。即要求我们要尽量保证轨迹规划得到的轨迹点位置距离定点的欧氏距离足够小，直到满足焊接机器人绕定点转动的工作精度要求。
经过多次实验发现，对于一个大的绕定点转动的位姿变化，即当一个完整变换比较大时（指初始状态和目标状态相差较大时），我们可以通过将一个完整变换分割为多个子步骤，让每一步变换变小，再对每个子步骤轨迹规划，能够有效提高轨迹规划的精度。举一个具体的例子，“以初始状态和目标状态为两端点，让机械臂末端绕定点转动pi/2”，可以将该变换分成 5 个变换子步骤（缩小初始状态和目标状态的位置和姿态的相差值），每个步骤以 10 为规划步数，再在每个子步骤中调用轨迹插值函数，得到规划的轨迹。
本着不造轮子的精神，我们直接调用matlab robotics toolbox来实现机械臂末端绕定点转动，代码如下：

%% 说明：该实现绕定点转动的规划轨迹，进行可视化呈现
clear;
clc;
% %建立机器人模型
%        theta    d        a        alpha     offset
L1=Link([pi/2     85       27       -pi/2     0     ]); %定义连杆的D-H参数
L2=Link([-pi/2    0        102      0         0     ]);
L3=Link([0        0        20       -pi/2     0     ]);
L4=Link([0        96       0         pi/2     0     ]);
L5=Link([0        0        0        -pi/2     0     ]);
L6=Link([0        39       0        0         0     ]);
robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','manji'); %连接连杆，机器人取名manji
robot.display();
theta=[pi/2,-pi/2,0,0,0,0];%指定的关节角
%% 正运动学验证与仿真
p0=robot.fkine(theta) %fkine正解函数，根据我们给定的关节角theta，求解出末端位姿p
%% 逆运动学验证与仿真
q0=robot.ikine(p0) %ikine逆解函数，根据我们给定的末端位姿p，求解出关节角qangle=1/3*pi;
robot.plot(q0);

%% 变量初始化
num=5; % 将步骤分为子步骤的数量
step=10; % 每个子步骤轨迹规划的步数
Q=[]; %存储所有关节的角度变化
QD=[];%存储所有关节的角速度变化
QDD=[];%存储所有关节的角加速度变化
x=[]; %存储所有关节的角度变（可视化动作）

T1=transl(0,200,150); %根据给定起始点，得到起始点位姿
T2=transl(0,200,150); %根据给定终止点，得到终止点位姿
R0=rotx(-pi/2)*rotz(-pi/2);  %初始坐标系位姿 
% 将初始坐标系位姿赋给起始点和终止点
for i=1:3
    for j=1:3
        T1(i,j)=R0(i,j);
    end
end

%% 绕Y轴旋转2*pi/3的轨迹规划
angle=2*pi/3; % 绕Y轴旋转的角度
for m=0:num-1
    % 将变换的起始位姿赋给初始位姿
    c=R0*roty(m/num*angle);       
    for i=1:3
        for j=1:3
            T1(i,j)=c(i,j);
        end
    end
    % 将变换的终止位姿赋给目标位姿
    c=R0*roty((m+1)/num*angle);
    for i=1:3
        for j=1:3
            T2(i,j)=c(i,j);
        end
    end
    q1=robot.ikine(T1);%根据起始点位姿，得到起始点关节角
    q2=robot.ikine(T2);%根据终止点位姿，得到终止点关节角
    [q ,qd, qdd]=jtraj(q1,q2,step); %五次多项式轨迹，得到关节角度，角速度，角加速度，50为采样点个数
    Q=[Q;q(2:step,:)]; %将所有的关节角度赋值
    QD=[QD;qd(2:step,:)];%将所有的关节角速度赋值
    QDD=[QDD;qdd(2:step,:)]; %将所有的关节角加速度赋值
end
% 角度变化赋值给x
x=[x;Q];
for i=1:(step-1)*num
    x=[x;Q((step-1)*num+1-i,:)];
end

%% 画出机械臂的轨迹变化
robot.plot(x);

得到绕定点转动的效果如下图：

4 求解每个关节的角度、角速度和角加速度曲线

利用插值函数求解机械臂的轨迹规划，再利用matlab robotics toolbox求解机械臂运动过程中每个关节的角度、角速度和角加速度变化的曲线。代码如下：

%% 说明：该程序对机械臂的规划轨迹进行可视化呈现
% 可视化所有关节的角度变化曲线、角速度变化曲线、角加速度变化曲线
clear;
clc;
% %建立机器人模型
%        theta    d        a        alpha     offset
L1=Link([pi/2     85       27       -pi/2     0     ]); %定义连杆的D-H参数
L2=Link([-pi/2    0        102      0         0     ]);
L3=Link([0        0        20       -pi/2     0     ]);
L4=Link([0        96       0         pi/2     0     ]);
L5=Link([0        0        0        -pi/2     0     ]);
L6=Link([0        39       0        0         0     ]);
robot=SerialLink([L1 L2 L3 L4 L5 L6],'name','manji'); %连接连杆，机器人取名manji
robot.display();

%%
num=1; % 将步骤分为子步骤的数量
step=50; % 每个子步骤轨迹规划的步数
error=[];% 存储规划轨迹上的点和定点的欧氏距离，作为误差
error_matrix=zeros(3,num*(step-1)); % 存储规划轨迹上的点的XYZ坐标
Q=[]; %存储所有关节的角度变化
QD=[];%存储所有关节的角速度变化
QDD=[];%存储所有关节的角加速度变化

angle=pi/2;
T1=transl(0,200,150);%根据给定起始点，得到起始点位姿
T2=transl(0,200,150);%根据给定终止点，得到终止点位姿
R0=rotx(-pi/2)*rotz(-pi/2); %初始坐标系位姿
% 将初始坐标系位姿赋给起始点和终止点
for i=1:3
    for j=1:3
        T1(i,j)=R0(i,j);
    end
end

for m=0:num-1
    c=R0*rotx(m/num*angle);       
    for i=1:3
        for j=1:3
            T1(i,j)=c(i,j);
        end
    end
    c=R0*rotx((m+1)/num*angle);
    for i=1:3
        for j=1:3
            T2(i,j)=c(i,j);
        end
    end
    q1=robot.ikine(T1);%根据起始点位姿，得到起始点关节角
    q2=robot.ikine(T2);%根据终止点位姿，得到终止点关节角
    [q ,qd, qdd]=jtraj(q1,q2,step); %五次多项式轨迹，得到关节角度，角速度，角加速度，50为采样点个数
    Q=[Q;q(2:step,:)]; %将所有的关节角度赋值
    QD=[QD;qd(2:step,:)];%将所有的关节角速度赋值
    QDD=[QDD;qdd(2:step,:)]; %将所有的关节角加速度赋值
end
T=robot.fkine(Q);%根据插值，得到末端执行器位姿

% 得到图像的横坐标
t=[];
for i=1:(num*(step-1))
    t=[t,i];
end

%% 画出所有关节的角度变化曲线、角速度变化曲线、角加速度变化曲线
% L1、……、L6表示关节1、2、……、6的角度
L1=Q(:,1);
L2=Q(:,2);
L3=Q(:,3);
L4=Q(:,4);
L5=Q(:,5);
L6=Q(:,6);
% K1、……、K6表示关节1、2、……、6的角速度
K1=QD(:,1);
K2=QD(:,2);
K3=QD(:,3);
K4=QD(:,4);
K5=QD(:,5);
K6=QD(:,6);
% M1、……、M6表示关节1、2、……、6的角加速度
M1=QDD(:,1);
M2=QDD(:,2);
M3=QDD(:,3);
M4=QDD(:,4);
M5=QDD(:,5);
M6=QDD(:,6);

% 画出关节1、2、……、6的角度变化曲线
figure(1)
subplot(2,3,1)
plot(t,L1);
title('angle of joint 1');
hold on
subplot(2,3,2)
plot(t,L2);
title('angle of joint 2');
hold on
subplot(2,3,3)
plot(t,L3);
title('angle of joint 3');
hold on
subplot(2,3,4)
plot(t,L4);
title('angle of joint 4');
hold on
subplot(2,3,5)
plot(t,L5);
title('angle of joint 5');
hold on
subplot(2,3,6)
plot(t,L6);
title('angle of joint 6');

% 画出关节1、2、……、6的角速度变化曲线
figure(2);
subplot(2,3,1)
plot(t,K1);
title('angle velocity of joint 1');
hold on
subplot(2,3,2)
plot(t,K2);
title('angle velocity of joint 2');
hold on
subplot(2,3,3)
plot(t,K3);
title('angle velocity of joint 3');
hold on
subplot(2,3,4)
plot(t,K4);
title('angle velocity of joint 4');
hold on
subplot(2,3,5)
plot(t,K5);
title('angle velocity of joint 5');
hold on
subplot(2,3,6)
plot(t,K6);
title('angle velocity of joint 6');

% 画出关节1、2、……、6的角速度度变化曲线
figure(3);
subplot(2,3,1)
plot(t,M1);
title('angle acceleration of joint 1');
hold on
subplot(2,3,2)
plot(t,M2);
title('angle acceleration of joint 2');
hold on
subplot(2,3,3)
plot(t,M3);
title('angle acceleration of joint 3');
hold on
subplot(2,3,4)
plot(t,M4);
title('angle acceleration of joint 4');
hold on
subplot(2,3,5)
plot(t,M5);
title('angle acceleration of joint 5');
hold on
subplot(2,3,6)
plot(t,M6);
title('angle acceleration of joint 6');

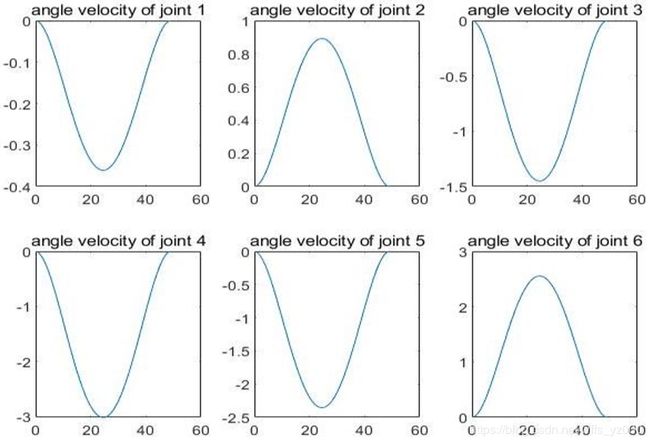
所有关节 1、2、3、4、5、6 的角度变化曲线、角速度变化曲线、角加速度变化曲线如下图：

如果对您有用别忘了点赞哦！