【立体视觉（一）】由基本矩阵、本质矩阵恢复摄像机矩阵——Structure from motion

最近在研究立体视觉，已经有一些日子了。相关理论对数学要求有点高，看了很久才有了一些系统的了解，并做了一些实验帮助理解。

本文会介绍Structure from motion中，利用两视图恢复相机位姿的内容，这也是三维重建的基础。

本文主要基于《Multiple View Geometry in Computer Vision(计算机视觉中的多视图几何)》这本书来梳理算法流程，有部分推导过程没有给出，读者可自行查阅

刚开始写微博，经验很少，不足之处，还请各位指导，如有错误，恳请指正。希望能向大家多多学习，共同研究和进步。

----------------------------------------------------------------------------------------------------------------------------------------------------------

条件：已获取相机在两不同位置拍摄的图像，没有空间标定物，可以不进行摄像机的标定；

目标：求出相机在3D空间中的摄像机矩阵，以便用于三维重构；

缺陷：在上述条件下，获得的摄像机矩阵与实际相差一个射影变换。

0、基础知识和参数

    射影变换和单应性矩阵：

射影变换过程中不变的性质有共点、共线、相交等，单应性矩阵H可以用来表示射影变换，并且通过H矩阵联系起来的对应点是唯一的。

    摄像机矩阵P：

摄像机矩阵由内参数矩阵K和外参数矩阵[R|t]组成，简单来说，P=K[R|t]。对于空间中的一个3D点X，其在图像上的投影为x=PX。

    齐次坐标：

本文中用的都是齐次坐标，不懂的童鞋可以自行查阅齐次坐标的定义和性质。

1.对极几何

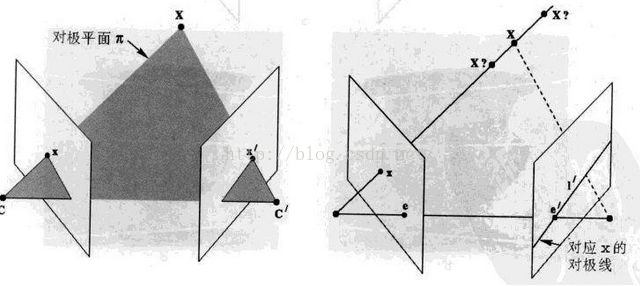
    摄像机中心在C和C‘时分别采集两幅图像，如图（a），空间中的一点X在平面上的投影x和x'，即为空间点X与摄像机中心c和c'连线和成像平面的交点。

    图（b）中展示了成像过程中的数学关系。其中，摄像机中心的连线与成像平面的交点e和e'为对极点（也是摄像机中心在另一平面上的投影）。若已知左图的摄像机中心C、成像点x，则可以确定C，x，X三点所在的直线，该直线在右侧成像面的投影I’即为x对应的对极线。显然，X在右侧平面的投影x'在此对极线I‘上。

   

2.基本矩阵

    (1)几何推导

    由上图的投影关系我们可以知道，对于空间中任意一点X，在两平面中分别有唯一的点x和x'与其对应，换句话说，这两个平面点是射影等价的。因此可以找到一个单应矩阵H，使得

    x'=Hx（根据射影变换的性质）

    而在右图中，由对极点e'和成像点x'，可以表示出对极线

    I’=e'×x'（根据其次坐标的性质）

    这样，I‘=e'×Hx

    我们可以令基本矩阵

   F=e'×H，即I‘=Fx

    上式给出了基本矩阵F的定义，但是这又有什么用呢？直观上我们能感觉到，F可以表征左右两幅图的位置关系，但是仅仅使用上述的定义，并不能很好地确定这样的关系，因此，可以通过下面的代数推导来帮助理解

    （2）代数推导

    假设两幅图像的摄像机矩阵分别为P，P'，且P的伪逆矩阵为P^，因为摄像机矩阵中的外参数可以用来表征相机的空间位姿，所以，如果能求出F和P的关系，就能利用F来恢复相机位姿。

    我们已知左图摄像机中心C，和成像点X=P^x(由x=PX得到)

    则x'=P'X=P'P^x

    另外，空间中的摄像机中心C在右图中的投影即为对极点e'，因此

    e'=P'C

    由(1)中几何推导可知

    I’=e'×x'=e'×(P'P^x)=(P'C)×(P'P^x)=Fx

    根据几何推导中的定义，可以得出F=e'×(P'P^)

    当然，上述定义中，我们已经可以发现，F与两摄像机矩阵有关，几何推导中的单应矩阵H也可以用(P'P^)来表示，但是我们仍然需要更为定量的描述，因为P中还有内参数的K影响，我们希望将这部分的影响分离出来，而确定F和R,t的关系。

    因为我们的目标是求解两幅图在三维空间中的相对位置关系，因此这里我们假设C即为世界坐标系的原点且其所在的坐标系为世界坐标系，则可以描述为

    P=K[I|0]    P'=K'[R|t]  

    P^{^}=(K^-1 0^T)^T

    两摄像机的中心分别为 (0 1)^T和(-R^Tt 1)^T，这是用齐次坐标表示的点。

    则由中心点和摄像机矩阵可以分别确定两个对极点e，e'

    e=P(-R^Tt  1)^T=KR^Tt

    e’=P’(0 1)^T=K’t

    则F=e'×(P'P^)=e'×K'RK^-1=(K’t)×K'RK^-1

    ^{这里需要用到参考资料中的结论A3.3，感兴趣的同学可以去研究其推导过程}

   ^{由A3.3我们可以得到F=(K’t)×K'RK-1}=K’^-Tt×RK^-1

    ^{到这里，我们已经可以发现，在已知内参数的情况下，是可以直接得到F和R，t的关系的。具体做法可以通过由本质矩阵的特性进行恢复。}

   另外，由于x'一定在极线I‘=Fx上，因此，根据齐次坐标的性质，x'^TFx=0。因此，在得到了两幅图像的对应点后，可以根据算法来求出F，具体解法较多，这里暂不研究。

3.由基本矩阵恢复摄像机矩阵

根据对极点的性质，e’^TF=0且Fe=0（e,e'为左右两个极点）

参考文献中给出了已知基础矩阵时，摄像机矩阵的表示（具体推导可自行翻阅）

P=[I|0]和P’=[e’ ×F|e’]

其中，e’是满足e’F=0的对极点。  

^{4.摄像机射影多义性}

    ^{了解到上述内容后，我们似乎已经能够求出摄像机矩阵P，但是我们开始就已经说过，类似的恢复与实际情况相差一个射影变换，那主要问题是出在哪里呢？}

    ^{回到2.(2)中对于基本矩阵的代数推导}

    ^{该过程中，我们是由摄像机矩阵P,P‘去推导基本矩阵F，并发现一对摄像机矩阵唯一确定一个F，但是反过来却不成立。}

    ^{设H为表示3维射影变换的矩阵}

    对于平面上的点x=PX=(PH)(H^-1X)，P’也存在类似关系

    则对于空间中的一点H^-1X，x和x'为其对应的成像点，同时PH和P‘H为其对应的摄像机矩阵。

    也就是说（P，P’）和（PH,P'H）对应的基础矩阵是相同的。

    

    同时，参考文献中还给出结论，在相差右乘一个射影变换H时，给定基本矩阵F，能唯一确定一对摄像机矩阵，且这种情况是唯一的。（换句话说，由F确定的P和P‘与实际相差一个射影变换H，即Pr=PH，Pr'=P'H）

    这样，利用上述方法恢复出的摄像机矩阵，与实际的摄像机矩阵一般都会相差一个射影变换

5.本质矩阵

    ^{本质矩阵可以认为是在归一化摄像机矩阵（内参数矩阵认为都是一样的）的情况下得到的基本矩阵。}

    ^{这里只要知道，本质矩阵E= t×R}

    ^{则很容易得到基本矩阵和本质矩阵的关系}

   ^E=K’TFK

    ^{因此在求出基本矩阵F和已知内参数矩阵的情况下，可以轻松得到本质矩阵E}

   ^{这里需要指出的是，本质矩阵没有内参数的作用，他比基本矩阵多了一些性质，从而能够完成下面部分中介绍的过程。因为是在归一化坐标系下的表示，所以E可以看作是对物理坐标的操作（不理解的话，可以只认为两者相差内参数K的关系），而F是对图像坐标的操作。}

   ^{由于去除了内参数的作用，因此利用本质矩阵的分解，可以得到与真实值相差一个尺度的相机外参（而不是相差一个射影变换）。具体求解过程如下。}

^{6.由本质矩阵恢复摄像机摄像机外参数}

    ^{这一部分则是应用了本质矩阵的性质以及一些数学推导了，下面只给出结论，具体推导过程可以查阅本文的参考资料。}

    ^{E= t×R并且我们希望能够得到其等价E=SR，从而用S去表征t}

    ^{根据参考文献中的结论，若E的SVD分解为Udiag(1,1,0)}V^{T，则E=SR可以有下面两种表示}

    S=UZU^T   R=UWV^T或者UW^TV^T

    同时文献中也证明了不存在其他的表示了。

    通过证明，得t=u3=U(0,0,1)^T

    ^{这里，为了求出摄像机矩阵，还有一个问题：}

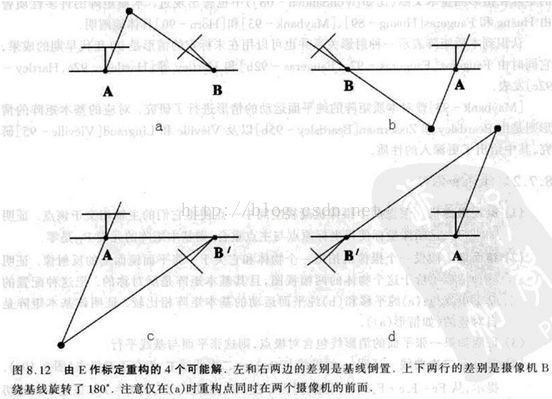
    ^{文献中指出，在上述SVD分解下，并且令第一个相机的坐标系为世界坐标系，则第二个摄像机矩阵有四种可能的情况;}

    

   ^{其分别对应的几何解释为}

    ^{也就是说，为了确定正确的摄像机矩阵，我们需要找到一个点，验证其是否是在两个摄像机的前边，就能排除其他三个解。}

7.总结

   这里，我们进行摄像机矩阵恢复的步骤为：

   找到图像中的对应点（特征点匹配）——计算基本矩阵F——计算摄像机矩阵

   如果我们得到了摄像机的内参数，而只求解外参数，则可以利用

   找到图像中的对应点（特征点匹配）——计算基本矩阵F——计算本质矩阵E——计算摄像机矩阵

   本文主要讲解了基本矩阵、本质矩阵、对极几何的相关理论，以及如何利用这些条件去恢复摄像机矩阵。

   这里，我们已经能够恢复出与实际相差一个射影变换的摄像机矩阵，接下来的任务，是如何利用这些条件，去获得三维重构。

   在不知道内参数的情况下，我们的方法是，尽可能恢复该射影变换，当然最后的结果会与实际结果相差一个尺度因子，但是已经能够正确构建实际场景的模型。如果知道内参，则可以利用本质矩阵直接分解得到外参。

   关于重构的内容，在接下来的学习中，我会继续将这部分更新。

参考文献《Multiple View Geometry in Computer Vision(计算机视觉中的多视图几何)》

最后更新于2015/8/31