莫队算法学习记录——Mo's Algorithm

先BB一通

今天XC讲了很多东西……可以从哲学层面分析——人的一切行为都是有目的性的，无目的性的行为不能称为有智能。

P.S.（阅读提示）

代码请复制到自己的代码编辑器中食用，因为CSDN代码框不具有实用性，也不能根据自己的思考更改代码，做注释。
对于粗体的字请认真阅读，一般都是重点内容或划分句子成分的。
（可能有彩蛋，请自行寻找）

学习记录

最近开始疯狂的补算法，什么LCT、AC-Automation、其中就包括了莫队算法。
@莫涛，前排膜拜dalao。
在网上找了很多资料，仔细斟酌后这位dalao的博客是比较优秀的。
这篇博客相对来说思路清晰，分析到位，辅以图示（我就很喜欢有的BLOG）。
建议结合两道例题食用：
普通莫队：P1494 [国家集训队]小Z的袜子
带修莫队：P1903 [国家集训队]数颜色

进入正题

莫队算法，是处理有关区间问题的离线算法。（这代表了国家队水平的暴力）
引入区间指针 [l,r] [ l , r ] ，通过区间之间的转移达到求解的效果，结合（国家队水平的）优化，缩减时间复杂度。

算法讲解

算法要点可拆分为区间转移与分块优化。

区间转移

若要将区间 [l,r] [ l , r ] 转移至区间 [l′,r′] [ l ′ , r ′ ] ，

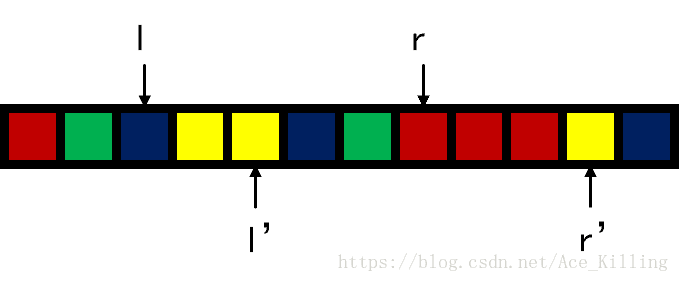
可将操作转化为区间 [l,r] [ l , r ] 转移至区间 [l+1,r] [ l + 1 , r ] 、 [l−1,r] [ l − 1 , r ] 、 [l,r+1] [ l , r + 1 ] 、 [l,r−1] [ l , r − 1 ]

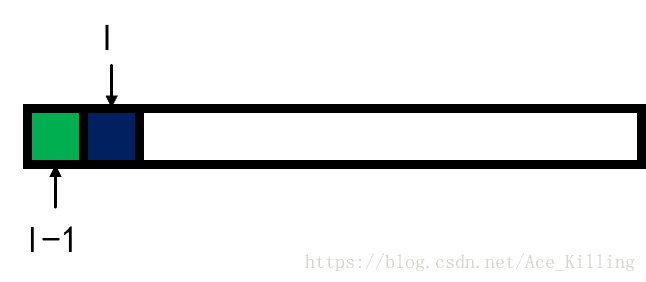
转移区间时可只讨论绿色方块造成的影响，实现 O(1) O ( 1 ) 转移。

分块优化

拿出笔记本！记重点！记重点！记重点！
莫队算法的优美就在于这个（国家队水平的）优化。
在离线算法中，我们常常使用排序的方法，来剔除枚举所消耗的冗余时间。
此优化基于分块思想，结合排序，将时间复杂度的指数缩小了。
对于两个询问，若在其 l l 在同块，那么将其 r r 作为排序关键字，若 l l 不在同块，就将 l l 作为关键字排序。使用 Bei B e i 数组表示i所属的块是谁。排序如：

证明：这个比较函数能够压缩时间复杂度
蒟蒻说：“并不会证明正确性。”
dalao说：“这个的正确性显然。”

排序后，就是简单的从一个区间到另一个区间，重复的操作。

普通莫队

给出一个序列，询问在区间 [l,r] [ l , r ] 中，任取的两数值相同的概率。（“两数”在严格意义上相异，即取了一数后不放回，再取一数）

有一种显然的做法是对于每个询问，暴力 O(n2) O ( n 2 ) 求解，在此不做讨论。
将莫队算法加入考虑范围。
每一次做区间转移，只涉及到一个位置的修改，所以在实现中仅仅改动修改答案的函数即可。
时间复杂度： O(n32) O ( n 3 2 )

//Ace_Killing Mo's-Algorithm
#include 
#include 
#include 
#include 
using namespace std;

struct node
{
    int l, r, t;
    long long A, B;
};

int n, m;
int c[50005];
int Be[50005], unit;
node q[50005];
int sum[50005];
long long ans;

bool cmp(node x, node y) {return Be[x.l] == Be[y.l] ? x.r < y.r : x.l < y.l;}
bool CMP(node x, node y) {return x.t < y.t;}
long long sqr(long long x) {return x * x;}
void Add(int pos, int value) {ans -= sqr(sum[c[pos]]), sum[c[pos]] += value, ans += sqr(sum[c[pos]]);}

long long Gcd(long long a, long long b)
{
    for (; a %= b;)
        swap(a, b);

    return b;
}

int main(int argc, char const *argv[])
{
    //freopen("init.in", "r", stdin);
    scanf("%d%d", &n, &m);
    unit = sqrt(n);

    for (int i = 1; i <= n; i++)
        scanf("%d", &c[i]), Be[i] = i / unit + 1;

    for (int i = 1; i <= m; i++)
        scanf("%d%d", &q[i].l, &q[i].r), q[i].t = i;

    sort(q + 1, q + m + 1, cmp);

    for (int i = 1, l = 1, r = 0; i <= m; i++)
    {
        for (; l < q[i].l; l++)
            Add(l, -1);

        for (; q[i].l < l; l--)
            Add(l - 1, 1);

        for (; r < q[i].r; r++)
            Add(r + 1, 1);

        for (; q[i].r < r; r--)
            Add(r, -1);

        if (q[i].l == q[i].r)
        {
            q[i].A = 0, q[i].B = 1;
            continue;
        }

        long long len = q[i].r - q[i].l + 1;
        q[i].A = ans - len;
        q[i].B = sqr(len) - len;
        long long tmp = Gcd(q[i].A, q[i].B);
        q[i].A /= tmp, q[i].B /= tmp;
    }

    sort(q + 1, q + m + 1, CMP);

    for (int i = 1; i <= m; i++)
        printf("%lld/%lld\n", q[i].A, q[i].B);

    return 0;
}

带修莫队

给出一个序列，要求满足以下两个操作：
  1.询问区间 [l,r] [ l , r ] 中有多少个不相同的值；
  2.修改序列中第 pos p o s 个数的值。

引入带修莫队。
思考带修莫队与普通莫队的关联性。
唯一的本质区别就是需要维护多一维时间序(Timing)。
简单修改普通莫队。
时间复杂度： O(n53) O ( n 5 3 )

#include 
#include 
#include 
#include 
using namespace std;

struct Query
{
    int l, r, t, Tim, ans;
};

struct Modify
{
    int pos, s, t;
};

int n, m;
int c[50005], f[50005];
int Be[50005], unit;
Query q[50005];
Modify d[50005];
int qt, dt;
int sum[1000005];
int l = 1, r, Tim, ans;

bool cmp(Query x, Query y) {return Be[x.l] == Be[y.l] ? (Be[x.r] == Be[y.r] ? x.Tim < y.Tim : x.r < y.r) : x.l < y.l;}
bool CMP(Query x, Query y) {return x.t < y.t;}
bool Get()
{
    int c = 0;

    for (c = getchar(); (c == ' ') || (c == '\r') || (c == '\n'); c = getchar());

    return c == 'Q';
}

void Add(int pos, int value)
{
    sum[pos] += value;

    if (value > 0)
        ans += sum[pos] == 1;

    if (value < 0)
        ans -= sum[pos] == 0;
}

void Goto(int pos, int value)
{
    if ((l <= pos) && (pos <= r))
        Add(value, 1), Add(c[pos], -1);

    c[pos] = value;
}


int main(int argc, char const *argv[])
{
    //freopen("init.in", "r", stdin);
    scanf("%d%d", &n, &m);
    unit = pow(n, 0.666666);

    for (int i = 1; i <= n; i++)
        scanf("%d", &c[i]), f[i] = c[i], Be[i] = i / unit + 1;

    for (int i = 1; i <= m; i++)
    {
        if (Get())//Question
        {
            int x, y;
            scanf("%d%d", &x, &y);
            q[++qt] = (Query) {x, y, qt, dt, 0};
        }
        else//Replace
        {
            int pos, value;
            scanf("%d%d", &pos, &value);
            d[++dt] = (Modify) {pos, f[pos], value};
            f[pos] = value;
        }
    }

    sort(q + 1, q + qt + 1, cmp);

    for (int i = 1; i <= qt; i++)
    {
        for (; Tim < q[i].Tim; Tim++)
            Goto(d[Tim + 1].pos, d[Tim + 1].t);

        for (; q[i].Tim < Tim; Tim--)
            Goto(d[Tim].pos, d[Tim].s);

        for (; l < q[i].l; l++)
            Add(c[l], -1);

        for (; q[i].l < l; l--)
            Add(c[l - 1], 1);

        for (; r < q[i].r; r++)
            Add(c[r + 1], 1);

        for (; q[i].r < r; r--)
            Add(c[r], -1);

        q[i].ans = ans;
    }

    sort(q + 1, q + qt + 1, CMP);

    for (int i = 1; i <= qt; i++)
        printf("%d\n", q[i].ans);

    return 0;
}

小结

莫队算法不单单倾向于一种固定的模式，其更像是一种数据结构，能够根据所需修改。（类似于CDQ分治）
莫队算法在处理区间统计类型问题具有十分强的能力，具备优秀的时空复杂度，同时具有十分强的适应性。
需要进行一段时间的深入思考，将其理解透彻。

                                                                       梦里殇此情高几楼
                                                                                           ——离人愁