数据降维-核化线性降维（kernelized PCA）

主要是在传统的PCA中加入了kernel。传统的PCA使用的是线性变换，为此(Schoelkopf et al. 1998)在传统的PCA中引进了kernel的技巧，本文的主要参考文献为MLAPP,参考的是第14章的第四小节，算法如下：

这个算法，和传统的pca差不多，主要步骤3和8主要是做特征空间的中心化，因为pca处理的是中心化后的数据，推断步骤如下： 

详细细节可以查看MLAPP这本书。

代码如下：

from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1234)
from scipy.spatial.distance import  pdist,squareform,cdist
fig=plt.figure()
ax=fig.gca(projection="3d")
#三组数据的均值
mean_list=([0,1,2],[4,3,5],[7,8,9])
#三组数据的方差
cov=np.array([[2,0,0],[0,1,0],[0,0,3]],dtype=np.float32)
#用来控制方差大小的参数
cita=[0.5,0.8,0.5]
sample=list()
for mean,cita in zip(mean_list,cita):
    #采样出三组数据
    data=np.random.multivariate_normal(mean,cov=cita*cov,size=100)
    sample.append(data)
label=["blue","orange","green"]
for P,label in zip(sample,label):
    ax.scatter(P[:,0],P[:,1],P[:,2],label=label,c=label)
ax.legend()
plt.show()
class KernelPCA:
    def __init__(self,bandwidth,dim):
        #定义核函数的带宽
        self.bandwidth=bandwidth
        #定义隐变量的维数
        self.dim=dim
    def fit(self,train_X):
        self.size_train=train_X.shape[0]
        self.train_X=train_X
        dist=squareform(pdist(self.train_X))
        K=self.rbf_kernel(dist)
        self.one=np.ones((self.size_train,1),dtype=np.float32)
        O=self.one.dot(self.one.T)/self.size_train
        #K~
        K_hat=K-O.dot(K)-K.dot(O)+O.dot((K.dot(O)))
        D,U=np.linalg.eig(K_hat)
        D=np.reshape(D,(self.size_train,))
        self.V=U[:,:self.dim]/D[:self.dim]
    def predict(self,data):
        pred_size=data.shape[0]
        O_x=np.ones((pred_size,1)).dot(self.one.T)/self.size_train
        K_x=self.rbf_kernel(cdist(data,self.train_X))
        #K~*
        K_h=K_x-O_x.dot(K_x)-K_x.dot(O_x)+O_x.dot(K_x.dot(O_x))
        z=K_h.dot(self.V)
        return z
    def rbf_kernel(self,X):
        return np.exp(-X/(self.bandwidth**2))
kp=KernelPCA(1,2)
#将三组数据连接起来
data=np.concatenate((sample[0],sample[1],sample[2]),axis=0)
kp.fit(data)
z=kp.predict(data)
a,b,c=np.split(z,3,axis=0)
latent_list=[a,b,c]
colors=["blue","orange","green"]
for z,color in zip(latent_list,colors):
    plt.scatter(z[:,0],z[:,1],c=color)
plt.show()

原始的三组数据如图：

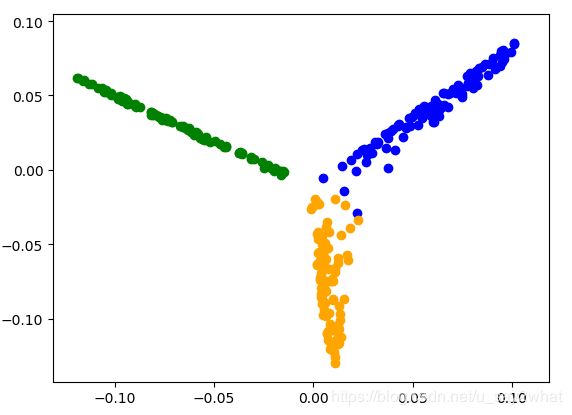
带宽为1，经过映射后为：

当然你可以调节不同的带宽值，带宽为4时：