博弈论——非完全信息扩展式博弈
版权声明:本文为原创文章,未经博主允许不得用于商业用途。
在扩展式博弈中,有些时候博弈的信息是不完全的:
- 玩家不知道其他玩家之前的决策
- 玩家不记得自己之前的决策
此时使用虚线连接这些信息集相同的决策点。
基本概念
- 非完全信息扩展式博弈表示为: G = { N , J , P , I , { u i } } G=\{N,J,P,I,\{u_i\}\} G={N,J,P,I,{ui}}
- 信息集: I = { I 1 , I 2 , . . . , I N } I=\{I_1,I_2,...,I_N\} I={I1,I2,...,IN}为所有玩家的信息集, I i = { I i 1 , I i 2 , . . . , I n i } I_i=\{I_{i1},I_{i2},...,I_{n_i}\} Ii={Ii1,Ii2,...,Ini}为玩家i的所有决策节点根据信息的划分。
- 信息集 I i I_i Ii中的每个元素为到达该玩家某一决策点或多个决策节点,使用从根节点到此节点的路径表示。
- 在完全信息博弈中每个元素只包含一个节点。
- 显然信息集某元素中的多个路径下候选决策集是相同的,记作 A ( I i j ) = A ( h ) = A ( h ′ ) , h , h ′ ∈ I i j A(I_{ij})=A(h)=A(h'),h,h'\in I_{ij} A(Iij)=A(h)=A(h′),h,h′∈Iij,因此才无法区分。
- P ( I i j ) P(I_{ij}) P(Iij)为在该处做出决策的玩家。
玩家1无法分辨玩家2所做决策,因此其信息集为 I 1 = { ϕ , { L A , L B } } I_1=\{\phi,\{LA,LB\}\} I1={ϕ,{LA,LB}},其中LA和LB具有相同的候选决策集{a,b}
玩家2为完美回忆的,其信息集为 I 2 = { L } I_2=\{L\} I2={L}
- 完美回忆(Perfect Recall):如果玩家i记住自己之前的所有决策则是完美回忆的。
- 如果所有玩家都是完美回忆的,则该博弈是完美回忆的。
- 纯策略(Pure Strategies):玩家i的纯策略定义为 a i ∈ A ( I i 1 ) × A ( I i 2 ) × . . . × A ( I i m ) a_i\in A(I_{i1})\times A(I_{i2})\times...\times A(I_{im}) ai∈A(Ii1)×A(Ii2)×...×A(Iim)
- 混合策略(Mixed Strategies):作用在该玩家纯策略上的概率分布函数。
- 行为策略(Behavioral Strategies):玩家i的一系列的概率分布函数 β i = { β i 1 ( I i 1 ) , β i 2 ( I i 2 ) , . . . , β i n i ( I i n i ) } \beta_i=\{\beta_{i1}(I_{i1}),\beta_{i2}(I_{i2}),...,\beta_{in_i}(I_{in_i})\} βi={βi1(Ii1),βi2(Ii2),...,βini(Iini)},其中 β i k \beta_{ik} βik为作用在 A ( I i k ) A(I_{ik}) A(Iik)决策集上的概率分布函数,其中 P ( I i k ) = i P(I_{ik})=i P(Iik)=i
- 从概率的角度,在行为策略中每次决策之间是相互独立的,而混合策略则可能不是相互独立的。
- 在完全信息博弈中,行为策略和混合策略可以相互转化,混合策略可以看作行为策略的联合分布函数。
- 库恩定理(Kuhn Theorem):在完美回忆的有穷扩展式博弈中,行为策略和混合策略可以相互转化,且采取行为策略和混合策略的结果是等价的。
- 子博弈:具有独立信息集的子树,即子树的任意节点不能和外部节点共用信息集,直观表示就是没有从子树内部到外部的虚线。
- 定理:完美回忆博弈至少有一个子博弈完美均衡(后向归纳)
- 信念(Belief):在非完全信息的扩展式博弈中的信念( μ \mu μ)是关于信息集的一组概率分布函数,如果信息集只有一个节点则概率为1。
- 贝叶斯一致性:信念符合贝叶斯定律。
- 一致性:信念是概率的极限。
- 评估(Assessment):评估记作 ( β , μ ) (\beta,\mu) (β,μ),可以评估一组信念和行为的一致性和贝叶斯一致性。且一致性可以推出贝叶斯一致性。
- 序惯理性(Sequential Rational):序列理性是建立在信念上的,即对于每个信息集上的信念,玩家i都做出最优决策。 ∀ I i j , u i ( β i , β − i ∣ I i j , μ ) ≥ u i ( β i ′ , β − i ∣ I i j , μ ) \forall I_{ij},u_i(\beta_i,\beta_{-i}|I_{ij},\mu)\geq u_i(\beta_i',\beta_{-i}|I_{ij},\mu) ∀Iij,ui(βi,β−i∣Iij,μ)≥ui(βi′,β−i∣Iij,μ)
- ( β , μ ) (\beta,\mu) (β,μ)是序贯均衡的如果其满足一致性和序贯理性。
- 完美回忆的有穷扩展式博弈一定有序惯均衡
- 序贯均衡中的行为策略是SPE
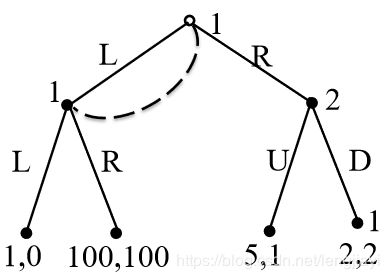
例题1
在此博弈中, I 1 = { ( ϕ , L ) } I_1=\{(\phi ,L)\} I1={(ϕ,L)}, I 2 = { R } I_2=\{R\} I2={R}, A ( I 11 ) = { L , R } , A ( I 21 ) = { U , D } A(I_{11})=\{L,R\}, A(I_{21})=\{U,D\} A(I11)={L,R},A(I21)={U,D}
因此纯策略有: { L U , L D , R U , R D } \{LU,LD,RU,RD\} {LU,LD,RU,RD},且收益为 u = { ( 1 , 0 ) , ( 1 , 0 ) , ( 5 , 1 ) , ( 2 , 2 ) } u=\{(1,0),(1,0),(5,1),(2,2)\} u={(1,0),(1,0),(5,1),(2,2)},显然R为Player1的严格占优策略,因此纳什均衡为(R,D)
如果使用行为策略,则设Player1的行为策略为 [ L , p ; R , 1 − p ] [L,p;R,1-p] [L,p;R,1−p],则收益期望为: U 1 = p 2 + p ( 1 − p ) × 100 + ( 1 − p ) × 2 U_1=p^2+p(1-p)\times 100+(1-p)\times 2 U1=p2+p(1−p)×100+(1−p)×2,当 p = 49 / 99 p=49/99 p=49/99时取得最大值 2599 11 ≃ 26.3 \frac{2599}{11}\simeq 26.3 112599≃26.3
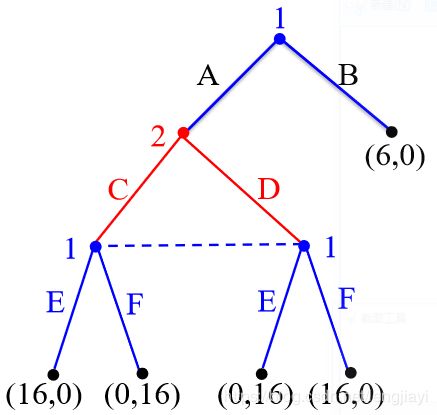
例题2
求序贯均衡
假设行为策略为 β = ( β 1 , β 2 ) = ( p , r ; q ) \beta=(\beta_1,\beta_2)=(p,r;q) β=(β1,β2)=(p,r;q),其中p,r,q为选择A,E,C的概率。
则由贝叶斯公式,Player1在 { A C , A D } \{AC,AD\} {AC,AD}处关于AC的信念为 μ = q \mu=q μ=q。
- 如果玩家2行为策略中,q=0,则 μ = 0 \mu=0 μ=0,玩家1将选择DF,则此时玩家2收益为0,非最优策略。
- 如果q=1,则 μ = 1 \mu=1 μ=1,玩家1将选择CE,同样不是最优策略。
- 如果 q ∈ ( 0 , 1 ) q\in (0,1) q∈(0,1),则玩家1收益为 u 1 = 16 μ r + 16 ( 1 − μ ) ( 1 − r ) = 16 − 16 q − 16 r ( 1 − 2 q ) u_1=16\mu r+16(1-\mu)(1-r)=16-16q-16r(1-2q) u1=16μr+16(1−μ)(1−r)=16−16q−16r(1−2q),且保证玩家2选择AC和AD的纯策略收益相同,即 16 ( 1 − r ) = 16 r ⇒ r = 1 / 2 16(1-r)=16r \Rightarrow r=1/2 16(1−r)=16r⇒r=1/2。
- 当 q > 1 / 2 q>1/2 q>1/2时, u 1 u_1 u1为r的增函数,因此r=1时收益最大。
- 当 q < 1 / 2 q<1/2 q<1/2时, u 1 u_1 u1为r的减函数,因此r=0时收益最大。
- q = 1 / 2 q=1/2 q=1/2时, r ∈ [ 0 , 1 ] r\in[0,1] r∈[0,1],即只有此时可以满足 r = 1 / 2 r=1/2 r=1/2,因此子博弈收益为(8,8)占优,因此p=1。