MATLAB 牛顿迭代法解非线性方程组
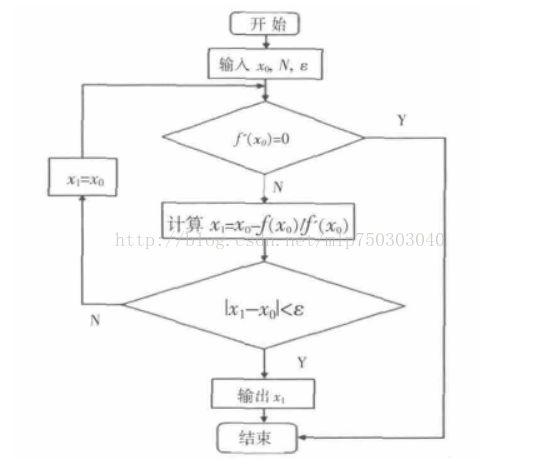
牛顿迭代法流程图:
Newton迭代法计算步骤 :
(1) 取初始点x0,最大迭代次数N和精 度 ε。
(2) 如果 f' (x0)=0, 则停止计算;否则计算 x1 = x0 -f(x0)/ f'(x0)。
(3) 如果|x1-x0|<ε, 则停止计算 ; 否 则 x0=x1, 转 到 (2)。
(4) 如果n=N, 则停止计算; 否 则 取 n=n+1, 转 到 (2)。
这里给出一个例子:
首先建立函数:
function f=F(x);
f(1)=x(1)^2-10*x(1)+x(2)^2+8;
f(2)=x(1)*x(2)^2+x(1)-10*x(2)+8;
f=[f(1) f(2)];
然后构建上一个函数的导函数,用于求方程组的雅克比矩阵:
function df=DF(x)
df=[2*x(1)-10,2*x(2); x(2)^2+1,2*x(1)*x(2)-10];
最后编写迭代的过程:
clear;
clc
x=[0,0]'; %指定初始值
f=F(x);
df=DF(x);
fprintf('%d %.7f %.7f\n',0,x(1),x(2));
N=4;
for i = 1:N
y=df\f';
x=x-y;
f=F(x);
df=DF(x);
fprintf('%d %.7f %.7f\n',i,x(1),x(2));
if norm(y)<0.0000001 %如果小于该精度,就结束
break;
else
end
end
因此整个流程还是很简单的,这里做一个总结,并给出一个模板。
第一步,用MATLAB写出方程组
function f=F(x);
f(1)=....
f(2)=....
f(3)=....
...
%将上面构造好的方程组加到[]中
f=[f(1) f(2) f(3) ...];
第二步:构造第一步函数的导函数
function df=DF(x)
%例子:df=[2*x(1)-10,2*x(2); x(2)^2+1,2*x(1)*x(2)-10];
%具体格式如下:
df=[函数f(1)的自变量x1的导数,函数f(1)自变量x2的导数 ;
函数f(2)的自变量x1的导数,函数f(1)自变量x2的导数 ;
...] %注意:这里用分号;去区别每个函数, 用逗号,来区别每个函数中的每个自变量。
第三步:写迭代的过程
clear;
clc
x=[0,0]'; %指定初始值,注意这里有几个变量,就写几个
f=F(x);
df=DF(x);
fprintf('%d %.7f %.7f\n',0,x(1),x(2));
N=4; %该值用来指定迭代的次数
for i = 1:N
y=df\f';
x=x-y;
f=F(x);
df=DF(x);
fprintf('%d %.7f %.7f\n',i,x(1),x(2));
if norm(y)<0.0000001 %指定结束的精度
break;
else
end
end
希望可以帮助到大家,下面的一个例子,是我之前做的,可能还没验证就丢上去了,大家不要当真,以我上面写的流程为主,注意在第二步求导函数的过程中,当然可以用MATLAB自带的求导函数求导,注意的就是要对每个自变量求导,其实就是偏导数。
function f=fun(x); %定义非线性方程组
syms x1 x2 x3 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15
p=1025;
g=9.8;
f1=-p*g*x1*pi+12000+sin(x2)*x3;
f2=-x3*cos(x2)+0.625*pi*(2-x1)*12*12;
f3=-x3*sin(x2)-pi*0.025*0.025*p*g+100+x(5)*sin(x6);
f4=-x3*cos(x2)+x5*cos(x6);
f5=-x5*sin(x6)-pi*0.025*0.025*p*g+100+x7*sin(x8);
f6=-x5*cos(x6)+x7*cos(x8);
f7=-x7*sin(x8)-pi*0.025*0.025*p*g+100+x9*sin(x10);
f8=-x7*cos(x8)+x9*cos(x10);
f9=-x9*sin(x10)-pi*0.025*0.025*p*g+100+x11*sin(x12);
f10=-x9*cos(x10)+x(11)*cos(x12);
a=0.625*12*12*pi*(2-x1);
f11=-0.15*0.15*p*g-x11*sin(x12)+1000+0.625*12*12*pi*(2-x1)*cosh(x13/a)*sin(x14)+12000;
f12=-x11*cos(x12)+0.625*12*12*pi*(2-x1)*cosh(x13/a)*cos(x14);
f14=-x1-(sin(x2)+sin(x6)+sin(x8)+sin(x10)+sin(x12))-x15+18;
f15=-x15+a-cosh(x13/a-1);
f16=-p*(pi*x(1)+0.025*0.025*pi*4+0.15*0.15*pi)+1000+40+100+1200;
f17=-cos(x14)+1/cosh(x13/a);
f=[f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 f14 f15 f16 f17];
function df=dfun1(x) %雅克比矩阵
f=fun(x);
df=[diff(f,'x1');diff(f,'x2');diff(f,'x3');diff(f,'x5');diff(f,'x6');diff(f,'x7');diff(f,'x8');diff(f,'x9');diff(f,'x10');diff(f,'x11');diff(f,'x12');diff(f,'x13');diff(f,'x14');diff(f,'x15')]; clear;clc
format;
x0=[0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1,0.1]; % 迭代初始值
eps = 0.0001; % 定位精度要求
for i = 1:1000
f = double(subs(fun(x0),{'x1' 'x2' 'x3' 'x5' 'x6' 'x7' 'x8' 'x9' 'x10' 'x11' 'x12' 'x13' 'x14' 'x15'},{x0(1) x0(2) x0(3) x0(4) x0(5) x0(6) x0(7) x0(8) x0(9) x0(10) x0(11) x0(12) x0(13) x0(14) }));
df = double(subs(dfun1(x0),{'x1' 'x2' 'x3' 'x5' 'x6' 'x7' 'x8' 'x9' 'x10' 'x11' 'x12' 'x13' 'x14' 'x15'},{x0(1) x0(2) x0(3) x0(4) x0(5) x0(6) x0(7) x0(8) x0(9) x0(10) x0(11) x0(12) x0(13) x0(14)})); % 得到雅克比矩阵
x = x0 - f/df;
if(abs(x-x0) < eps)
break;
end
x0 = x; % 更新迭代结果
end
disp('定位坐标:');
x
disp('迭代次数:');
i