FP增长树学习笔记

FP增长树学习笔记

此笔记参考书籍为数据挖掘导论

1.FP树表示法

FP树是一种输入数据的压缩表示，它将每个事务映射到FP树的一条路径来构造。不同的事物可能会有若干个相同的子项，因此它们的路径可能重叠，路径相互重叠越多，FP树的压缩效果越好。

FP树仅有一个根节点，用null标记。FP树有一个重要组成结构-头表，头表保存了所有的频繁项目，并且按照频率的降序排列，表中的每个项目包含一个节点链表，指向树中和它同名的节点。

创建FP树的方法：

首先创建树的根节点，用null标记，第一次扫描数据集，选出事物所有项中的频繁项，构建头表Flist。然后用下述方法扩充FP树。

扩充FP树的方法：

(1)扫描一次数据集，确定支持度计数，根据预先设定的最小支持度，丢弃非频繁项，并将频繁项按照支持度的递减排序。

(2)第二次扫描数据集，开始读入事务，并对每个事物创建一个分枝。

(3)当一个事务考虑增加分枝的时候，沿共同前缀上的每个节点的计数加1，为跟随前缀后的项创建节点并连接。

(4)头表连接在树中出现的每个同名节点。

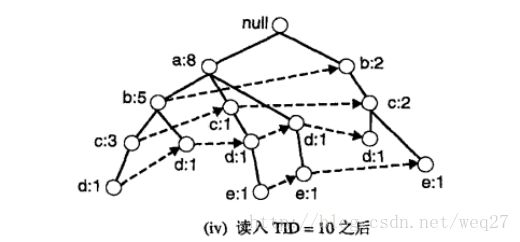
FP树生成示例图：

(图片来自数据挖掘导论一书)

2.FP增长算法的频繁项集的产生

FP增长算法是一种自底而上方式探索树，由FP产生频繁项集的算法。之前提到的Apiori算法是广度优先的方式，而FP增长算法是深度优先方式。

简单的说apriori是先产生一批候选项集，再通过原数据集去过滤非频繁项集：先找A、B、C，检查一下通过了，再找AB、AC、AB，检查又通过了，再到ABC…这样的广度优先的方式。fp-growth是从FP树中找频繁项集：先找A，再在找包含A的路径里，找到B，就得到AB是频繁项集，再再包含AB的路径里，找到C，ABC也是频繁项集了，包含A的项集找完了，则将A节点删除，然后开始找B的，直至剩下标记为null的根节点为止，所以说FP增长算法是深度优先方式。

FP增长算法是一种自底向上的算法，在FP增长算法中，是先从结尾的节点开始的。根据头表和已经生成的FP树我们可以获得当前所有以某个元素结尾的结点指针。
在挖掘频繁项集的时候，类似于Apriori算法，FP增长算法从单项集出发每次增加一个元素。对于每一个频繁项集，我们获得这个频繁项集作为结尾的所有前缀路径（起点为根节点），这些路径的集合称为条件模式基。 FP增长算法对于每一个频繁项集以前缀路径构造一棵FP树，然后向当前的频繁项集中添加一个元素，然后以深度优先的策略递归的进行这个过程知道发现所有频繁项集。

FP增长算法示例图：

(图片来自数据挖掘导论一书)

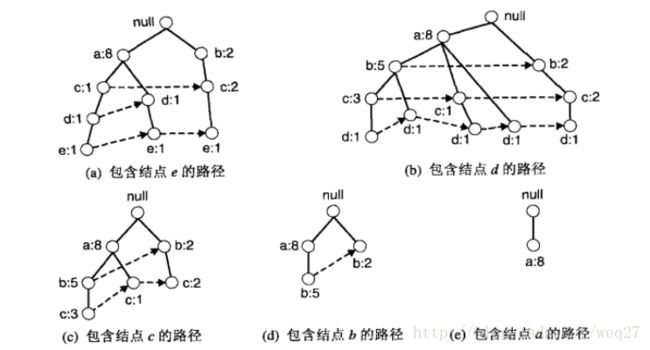
图片是按照前文的图iv来实现FP增长算法的，给定算法首先查找最底层的以e为后缀的频繁项集，接下来依次是d，c，b，最后是a。

以节点e为例：

1.首先收集包含e节点的所有路径，这些路径称为前缀路径，计算e的支持度计数，若e频繁，则将e并入频繁项集，并考虑de，ce，be和ae结尾的频繁项集的子问题。

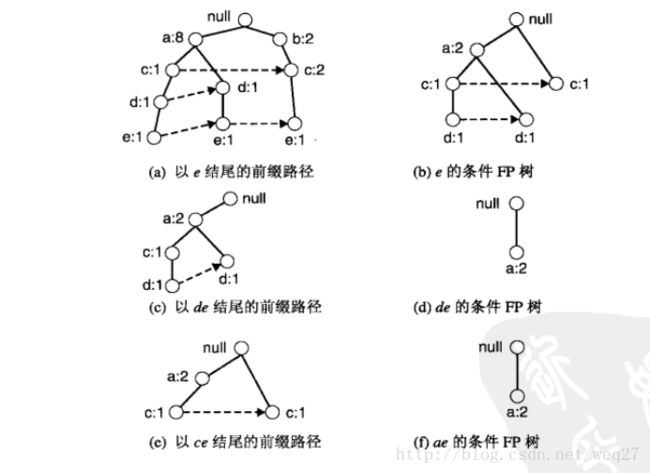
2.调整前缀路径的计数将其转化为条件FP树，例如e的条件FP树只包含e的事件，如下图b所示（我觉得下图b是有误的，根节点和节点c之间应该有个计数为1的b节点）。通过e的条件FP树，可以得到以de，ce，be和ae结尾的前缀路径，通过表头和节点计数，可以计算de，ce，be和ae的支持度计数，若其中de，ce和ae符合，将de，ce和ae加入频繁项集，并考虑de，ce结尾的频繁项集的子问题（ae不能继续扩展了，没有一个3-项集以ae结尾）。

3.将以de，ce结尾的前缀路径修改为de，ce的条件树，计算ade，ace，bce的支持度计数，ade是频繁的，将其并入频繁项集，此时ade不能继续扩展了，没有一个4-项集以ade结尾。

4.以e为后缀的频繁项集全部找出来了，删除FP树上的e节点，开始查找此时最底层的以d为后缀的频繁项集。