Noip2014 Day2 T2 寻找道路（最短路）

题目描述

在有向图G 中，每条边的长度均为1 ，
现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

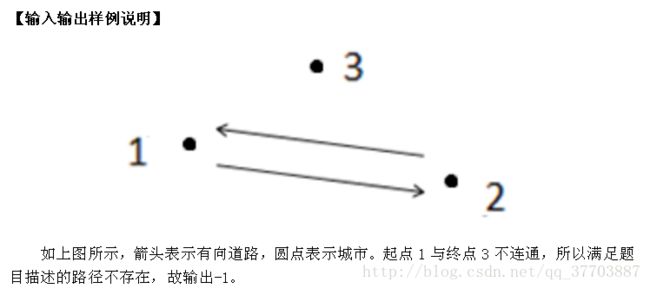
输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

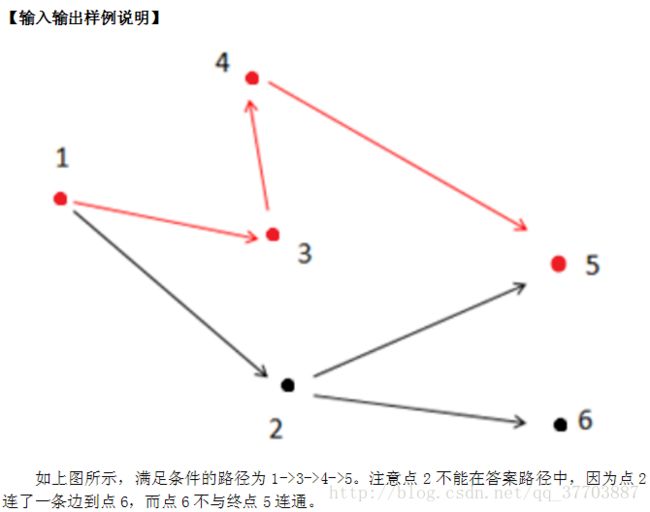
输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

解释2：

对于30%的数据，0< n ≤10，0< m ≤20；

对于60%的数据，0< n ≤100，0< m ≤2000；

对于100%的数据，0< n ≤10,000，0< m ≤200,000，0< x,y,s,t≤n，x≠t。

思路

刚看看题的时候有点懵，不知道从何下手

但是后来读懂题目之后觉得也不是特别的难（毕竟是第二题嘛~~）

条件一其实就是在告诉我们，我们最后求出最短路上的点一定都与终点相连

那我们只需要先将所有不与终点相通的点从图上剔除再找最短路就好了

对于剔除多余的点，这里我们很容易就想到了建立反图从终点出发用数组标记进行BFS

这样我们就得到了所有能形成最短路的点，再从起点出发走一遍SPFA，问题解决

代码

#include
#include
#define Maxn 10010
using namespace std;
int v[400020],next[400020]; //邻接表，没有写结构体的原因是要清零
int t,n,m,ss,tt,tot;
int h[Maxn],l[400020],r[400020];
int q1[Maxn],d[Maxn];
bool judge[Maxn],vis[Maxn],p[Maxn];
void add(int from,int to)
{
    v[++t]=to;
    next[t]=h[from];
    h[from]=t;
}
void bfs(int x)
{
    int head=0,tail=1;
    q1[1]=x;
    vis[x]=1;
    p[x]=1;
    tot++;
    while(headint now=q1[++head];
        for(int i=h[now];i;i=next[i])
        {
            int to=v[i];
            if(!vis[to])
            {
                vis[to]=1;
                q1[++tail]=to;
                tot++;
                p[to]=1;
            }
        }
    }
} //广搜找点，p数组就是标记数组 
void spfa(int x)
{
    int head=0,tail=1;
    q1[1]=x;
    memset(d,0x3f,sizeof d);
    d[x]=0;
    while (headint now=q1[++head];
        vis[now]=0;
        for(int i=h[now];i;i=next[i]) 
        {
            int to=v[i];
            if(!p[to]) continue; 
            if(judge[to]) continue;
            if(d[to]>d[now]+1) 
            {
                d[to]=d[now]+1;
                if (!vis[to]) 
                {
                    vis[to]=1;
                    q1[++tail]=to;
                }
            }
        }
    }
}
void init()
{
    memset(q1,0,sizeof q1);
    memset(vis,0,sizeof vis);
    memset(h,0,sizeof h);
    t=0;
} 
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++) scanf("%d%d",&l[i],&r[i]);
    scanf("%d%d",&ss,&tt);
    for(int i=1;i<=m;i++) add(r[i],l[i]); //反向建图 
    bfs(tt);
    if(!p[ss])
    {
        printf("-1");
        return 0;
    } //如果找不到起点证明没有答案 
    for(int i=1;i<=n;i++)
    {
        if(p[i]) continue;
        for(int p=h[i];p;p=next[p]) 
        {
            int q=v[p];
            judge[q]=1; //把一条路线上的点都标记 
        }
    }
    init(); //清零，很关键很关键 
    for(int i=1;i<=m;i++) add(l[i],r[i]); //正向建图 
    spfa(ss); //找最短路 
    printf("%d",d[tt]);
    return 0;
}