顺序最小优化算法(SMO)

引言:顺序最小优化(sequnential minimal optimal)算法由John Platt提出，可以高效地求解SVM的对偶问题。在此之前，我们先了解一下坐标上升算法

1. 坐标上升算法

如何解决下面的这个无约束优化问题：

maxαW(α1,α2,…,αm).

W 是以 αi 为变量的函数，我们用一种称为“坐标上升”的算法来求解它：

Loop until convergence:{For i=1,…,m {αi:=arg maxα^W(α1,…,αi−1,αi^,αi+1,…,αm).}}

在这个算法的最内层循环中，我们固定其余变量，只修改 αi 的值，以这种方式优化 W 。在当前的版本中优化的顺序是从 α1→αm ，但是在更复杂的算法中，我们可以调整这个顺序，比如按 W 变化最大的顺序优化 α 。

当我们以这种形式优化 W 函数，坐标上升法将会是一个相当高效地算法。下面的图片描绘了坐标上升的运行过程：

图中的椭圆代表二次函数的等高线，坐标上升算法从 (2,−2) 点开始运行，直至全局最优解。我们注意到它运行的每一步轨迹都垂直于坐标轴，这代表它每次只对一个变量进行优化。

---

2. SMO

这是我们之前经过L1正规化之后，推导出的对偶问题：

maxα s.t. W(α)=∑i=1mαi−12∑i,j=1my(i)y(j)αiαj⟨x(i),x(j)⟩0≤α≤C, i=1,…,m∑i=1mαiy(i)=0,(1)(2)(3)

假设我们有一组满足约束(2),(3)的 αi ，现在我们固定 α2,α3,…,αm ，只更改 α1 的值，依次顺序执行参数优化，我们可以得到 W(α) 的最优解吗？结果是不能！因为约束(3)保证了 α1 可由其他 αi 唯一确定：

α1y(1)=−∑i=2mαiy(i)⇒α1=−y(1)∑i=2mαiy(i)

因此如果我们想修改某个 αi 的值必须同时修改至少两个变量才能满足约束。据此我们确定SMO算法：

Repeat until convergence:{1.Select some pair αi and αj to update next (using a heuristic that tries to pick the two that will allow us to make the biggest progresstowards the global maximun).2.Reoptimize W(α) with respect to αi and αj, while holding all theother α′ks (k≠i,j) fixed.}

为了测试算法是否收敛，我们可以测算KKT条件是否小于容忍限 tol 。它的值通常在0.01到0.001之间（可以查看Platt的文章）。SMO算法高效的原因是因为求解 αi,αj 的过程十分高效，现在我们来简单推导一下。

假设我们有一组满足约束(2),(3)的 αi ，现在我们固定 α3,…,αm ，只更改 α1,α2 的值，重新优化 W(α1,…,αm) ，由公式(3)可得：

α1y(1)+α2y(2)=−∑i=3mαiy(i)

由于方程的右边是固定的，我们可以把它看成一个常量 ζ ，则上式可改写成：

α1y(1)+α2y(2)=ζ(4)

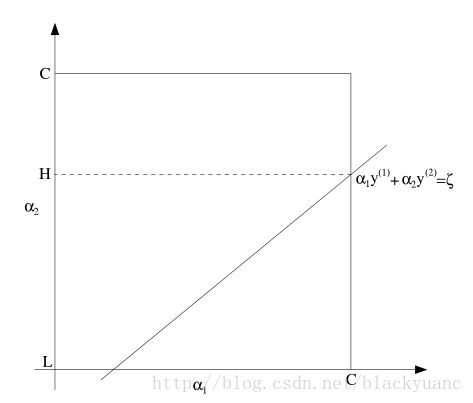
由约束(2)和上式我们可以绘制下图：

如图所有， α2 的取值范围只能是L到H，否则 αi,αj 的值无法同时满足范围约束和直线约束。由公式(4)我们可以推导得出：

α1=(ζ−α2y(2))y(1)

将上式回带至 W(α) 中可得：

W(α1,α2,…,αm)=W((ζ−α2y(2))y(1),α2,…,αm).

上式是一个关于 α2 的二次多项式，可以求解出 α2 ，若 α2 大于H则令其等于H，若 α2 小于L令其等于L，不属于一上两种情况则无需裁剪，至此确定了 α2 的值，带入公式(4)中求解 α1 。

有两点需要阅读Platt的论文弄清楚：如何通过启发式算法选取下一次更新的 αi,αj ？运行SMO时如何更新截距 b ？