Ceres-Solver库使用（四）-- 一些例子

Powell函数

下面来考虑一下稍微复杂一些的Powell函数最小化问题。记 x=[x1,x2,x3,x4] 有

f1(x)f2(x)f3(x)f4(x)F(x)=x1+10x2=5√(x3−x4)=(x2−2x3)2=10−−√(x1−x4)2=[f1(x), f2(x), f3(x), f4(x)]

我们希望找到合适的 x 值，使得 12∥F(x)∥2 最小。

同样，第一步我们定义计算函数每一分量值的算子，这里以 f4(x1,x2) 为例，代码如下：

struct F4 {
  template <typename T>
  bool operator()(const T* const x1, const T* const x4, T* residual) const {
    residual[0] = T(sqrt(10.0)) * (x1[0] - x4[0]) * (x1[0] - x4[0]);
    return true;
  }
};

类似的，我们可以定义类 F2 ， F3 和 F4 对应于算子 f1(x1,x2) ， f2(x3,x4) 和 f3(x2,x3) 。通过这些类，问题可以写作如下：

double x1 =  3.0; double x2 = -1.0; double x3 =  0.0; double x4 = 1.0;

Problem problem;

// Add residual terms to the problem using the using the autodiff
// wrapper to get the derivatives automatically.
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F1), NULL, &x1, &x2);
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F2), NULL, &x3, &x4);
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F3), NULL, &x2, &x3)
problem.AddResidualBlock(
  new AutoDiffCostFunction1, 1, 1>(new F4), NULL, &x1, &x4);

注意到每个ResidualBlock只依赖于两个参数而不是所有四个变量，运行计算我们可以得到如下结果：

Initial x1 = 3, x2 = -1, x3 = 0, x4 = 1
iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  1.075000e+02    0.00e+00    1.55e+02   0.00e+00   0.00e+00  1.00e+04       0    4.95e-04    2.30e-03
   1  5.036190e+00    1.02e+02    2.00e+01   2.16e+00   9.53e-01  3.00e+04       1    4.39e-05    2.40e-03
   2  3.148168e-01    4.72e+00    2.50e+00   6.23e-01   9.37e-01  9.00e+04       1    9.06e-06    2.43e-03
   3  1.967760e-02    2.95e-01    3.13e-01   3.08e-01   9.37e-01  2.70e+05       1    8.11e-06    2.45e-03
   4  1.229900e-03    1.84e-02    3.91e-02   1.54e-01   9.37e-01  8.10e+05       1    6.91e-06    2.48e-03
   5  7.687123e-05    1.15e-03    4.89e-03   7.69e-02   9.37e-01  2.43e+06       1    7.87e-06    2.50e-03
   6  4.804625e-06    7.21e-05    6.11e-04   3.85e-02   9.37e-01  7.29e+06       1    5.96e-06    2.52e-03
   7  3.003028e-07    4.50e-06    7.64e-05   1.92e-02   9.37e-01  2.19e+07       1    5.96e-06    2.55e-03
   8  1.877006e-08    2.82e-07    9.54e-06   9.62e-03   9.37e-01  6.56e+07       1    5.96e-06    2.57e-03
   9  1.173223e-09    1.76e-08    1.19e-06   4.81e-03   9.37e-01  1.97e+08       1    7.87e-06    2.60e-03
  10  7.333425e-11    1.10e-09    1.49e-07   2.40e-03   9.37e-01  5.90e+08       1    6.20e-06    2.63e-03
  11  4.584044e-12    6.88e-11    1.86e-08   1.20e-03   9.37e-01  1.77e+09       1    6.91e-06    2.65e-03
  12  2.865573e-13    4.30e-12    2.33e-09   6.02e-04   9.37e-01  5.31e+09       1    5.96e-06    2.67e-03
  13  1.791438e-14    2.69e-13    2.91e-10   3.01e-04   9.37e-01  1.59e+10       1    7.15e-06    2.69e-03

Ceres Solver v1.11.0 Solve Report
----------------------------------
                                     Original                  Reduced
Parameter blocks                            4                        4
Parameters                                  4                        4
Residual blocks                             4                        4
Residual                                    4                        4

Minimizer                        TRUST_REGION

Dense linear algebra library            EIGEN
Trust region strategy     LEVENBERG_MARQUARDT

                                        Given                     Used
Linear solver                        DENSE_QR                 DENSE_QR
Threads                                     1                        1
Linear solver threads                       1                        1

Cost:
Initial                          1.075000e+02
Final                            1.791438e-14
Change                           1.075000e+02

Minimizer iterations                       14
Successful steps                           14
Unsuccessful steps                          0

Time (in seconds):
Preprocessor                            0.002

  Residual evaluation                   0.000
  Jacobian evaluation                   0.000
  Linear solver                         0.000
Minimizer                               0.001

Postprocessor                           0.000
Total                                   0.005

Termination:                      CONVERGENCE (Gradient tolerance reached. Gradient max norm: 3.642190e-11 <= 1.000000e-10)

Final x1 = 0.000292189, x2 = -2.92189e-05, x3 = 4.79511e-05, x4 = 4.79511e-05

其实很容易就看出该问题的最优解为 x1=0,x2=0,x3=0,x4=0 此时最优化目标函数值为0。而从上面的计算步骤可以看出，通过10次迭代，最优化的目标函数值已经约为 4×10−12 。

曲线拟合

到目前为止，我们看到的例子都是一些简单不含数据的优化问题，而最小二乘和非线性最小二乘问题的最初目的是为了曲线拟合数据。下面我们就来考虑曲线拟合问题。拟合数据采样与曲线 y=e0.3x+0.1 ，并增加了标准偏差为 σ=0.2 的高斯噪声。下面我们使用这些数据来拟合曲线

y=emx+c.

首先，我们定义一个模板对象来计算剩余函数值，

struct ExponentialResidual {
  ExponentialResidual(double x, double y)
      : x_(x), y_(y) {}

  template <typename T>
  bool operator()(const T* const m, const T* const c, T* residual) const {
    residual[0] = T(y_) - exp(m[0] * T(x_) + c[0]);
    return true;
  }

 private:
  // Observations for a sample.
  const double x_;
  const double y_;
};

不妨假定我们已经将数据读取存放在 2n 大小的一维数组data中，那么问题结构可以由每组数据的CostFunction组成：

double m = 0.0;
double c = 0.0;

Problem problem;
for (int i = 0; i < kNumObservations; ++i) {
  CostFunction* cost_function =
       new AutoDiffCostFunction1, 1, 1>(
           new ExponentialResidual(data[2 * i], data[2 * i + 1]));
  problem.AddResidualBlock(cost_function, NULL, &m, &c);
}

编译运行可以得到如下结果：

iter      cost      cost_change  |gradient|   |step|    tr_ratio  tr_radius  ls_iter  iter_time  total_time
   0  1.211734e+02    0.00e+00    3.61e+02   0.00e+00   0.00e+00  1.00e+04       0    5.34e-04    2.56e-03
   1  1.211734e+02   -2.21e+03    0.00e+00   7.52e-01  -1.87e+01  5.00e+03       1    4.29e-05    3.25e-03
   2  1.211734e+02   -2.21e+03    0.00e+00   7.51e-01  -1.86e+01  1.25e+03       1    1.10e-05    3.28e-03
   3  1.211734e+02   -2.19e+03    0.00e+00   7.48e-01  -1.85e+01  1.56e+02       1    1.41e-05    3.31e-03
   4  1.211734e+02   -2.02e+03    0.00e+00   7.22e-01  -1.70e+01  9.77e+00       1    1.00e-05    3.34e-03
   5  1.211734e+02   -7.34e+02    0.00e+00   5.78e-01  -6.32e+00  3.05e-01       1    1.00e-05    3.36e-03
   6  3.306595e+01    8.81e+01    4.10e+02   3.18e-01   1.37e+00  9.16e-01       1    2.79e-05    3.41e-03
   7  6.426770e+00    2.66e+01    1.81e+02   1.29e-01   1.10e+00  2.75e+00       1    2.10e-05    3.45e-03
   8  3.344546e+00    3.08e+00    5.51e+01   3.05e-02   1.03e+00  8.24e+00       1    2.10e-05    3.48e-03
   9  1.987485e+00    1.36e+00    2.33e+01   8.87e-02   9.94e-01  2.47e+01       1    2.10e-05    3.52e-03
  10  1.211585e+00    7.76e-01    8.22e+00   1.05e-01   9.89e-01  7.42e+01       1    2.10e-05    3.56e-03
  11  1.063265e+00    1.48e-01    1.44e+00   6.06e-02   9.97e-01  2.22e+02       1    2.60e-05    3.61e-03
  12  1.056795e+00    6.47e-03    1.18e-01   1.47e-02   1.00e+00  6.67e+02       1    2.10e-05    3.64e-03
  13  1.056751e+00    4.39e-05    3.79e-03   1.28e-03   1.00e+00  2.00e+03       1    2.10e-05    3.68e-03
Ceres Solver Report: Iterations: 13, Initial cost: 1.211734e+02, Final cost: 1.056751e+00, Termination: CONVERGENCE
Initial m: 0 c: 0
Final   m: 0.291861 c: 0.131439

从上面的迭代步骤可以看出，初始 m=0,c=0 时目标函数值为 121.173 ，通过13次迭代之后，ceres找到解为 m=0.291861,c=0.131439 ，此时目标函数值为 1.05675 。相比于初始模型的 m=0.3,c=0.1 有较大的差距，但这是不要紧，因为我们在生成数据时增加了噪声。事实上，如果你用初始模型的 m=0.3,c=0.1 使用噪声数据去计算目标函数值时会发现，其值比 1.082425 会更坏，如下图：

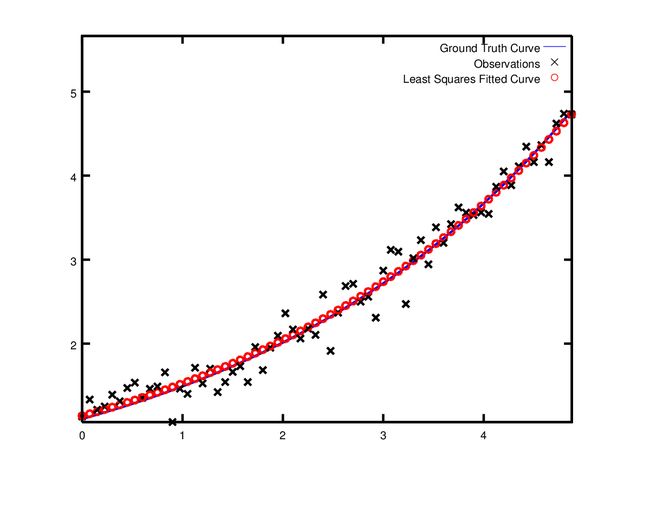
鲁棒的曲线拟合

现在假设如果我们给定的数据存在异常值，即有一些数据值不符合噪声模型的分布值。如果我们还是按照以上的方法去进行拟合的时候，我们可以得到下图，注意到图框上部边缘的两个点使得拟合曲线偏离实际曲线。

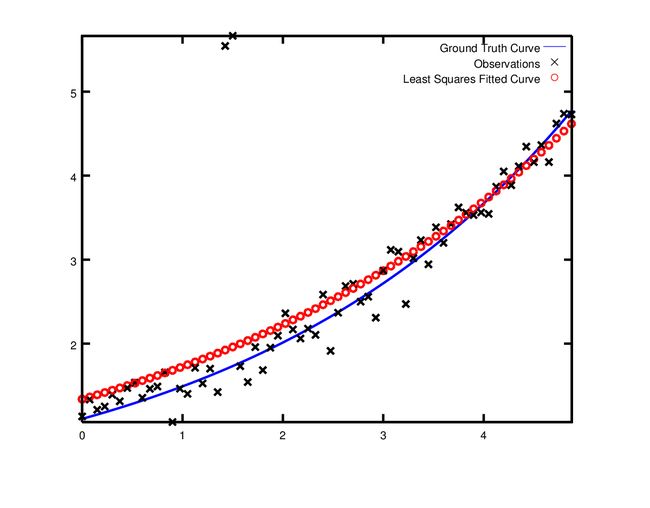
为了忽略这些异常点，ceres中一个标准的方法就是使用LossFunction。损失函数(Loss Function)会减少大的剩余值的影响，通常这些大的剩余值对应的就是异常点。我们将代码中的

problem.AddResidualBlock(cost_function, NULL , &m, &c);

替换为

problem.AddResidualBlock(cost_function, new CauchyLoss(0.5) , &m, &c);

CauchyLoss是ceres-solver库中提供的其中一种损失函数，参数 0.5 为损失函数的比例（以后会进一步阐明其意义）。由此，我们可以得到如下的结果：

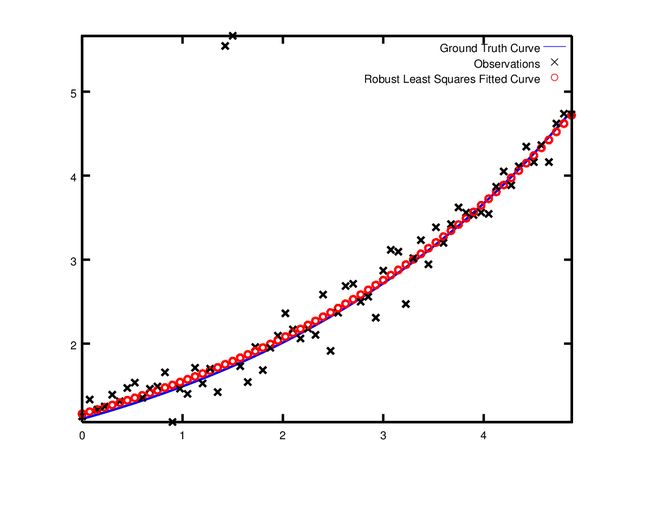
参考

http://www.ceres-solver.org/nnls_tutorial.html#powell-s-function