《动手学深度学习》pytorch版（第三次打卡）

cv方向

一、目标检测基础

1.目标检测和边界框

%matplotlib inline
from PIL import Image

import sys
sys.path.append('/home/kesci/input/')
import d2lzh1981 as d2l
# 展示用于目标检测的图
d2l.set_figsize()
img = Image.open('/home/kesci/input/img2083/img/catdog.jpg')
d2l.plt.imshow(img); # 加分号只显示图

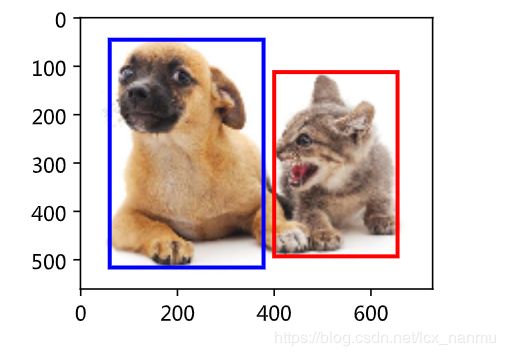
2.边界框

# bbox是bounding box的缩写
dog_bbox, cat_bbox = [60, 45, 378, 516], [400, 112, 655, 493]
def bbox_to_rect(bbox, color):  # 本函数已保存在d2lzh_pytorch中方便以后使用
    # 将边界框(左上x, 左上y, 右下x, 右下y)格式转换成matplotlib格式：
    # ((左上x, 左上y), 宽, 高)
    return d2l.plt.Rectangle(
        xy=(bbox[0], bbox[1]), width=bbox[2]-bbox[0], height=bbox[3]-bbox[1],
        fill=False, edgecolor=color, linewidth=2)

fig = d2l.plt.imshow(img)
fig.axes.add_patch(bbox_to_rect(dog_bbox, 'blue'))
fig.axes.add_patch(bbox_to_rect(cat_bbox, 'red'));

3.锚框

目标检测算法通常会在输入图像中采样大量的区域，然后判断这些区域中是否包含我们感兴趣的目标，并调整区域边缘从而更准确地预测目标的真实边界框（ground-truth bounding box）。不同的模型使用的区域采样方法可能不同。这里我们介绍其中的一种方法：它以每个像素为中心生成多个大小和宽高比（aspect ratio）不同的边界框。这些边界框被称为锚框（anchor box）。我们将在后面基于锚框实践目标检测。

注: 建议想学习用PyTorch做检测的童鞋阅读一下仓库a-PyTorch-Tutorial-to-Object-Detection。

4.生成多个锚框

假设输入图像高为 h ，宽为 w 。我们分别以图像的每个像素为中心生成不同形状的锚框。设大小为 s∈(0,1] 且宽高比为 r>0 ，那么锚框的宽和高将分别为 wsr√ 和 hs/r√ 。当中心位置给定时，已知宽和高的锚框是确定的。

下面我们分别设定好一组大小 s1,…,sn 和一组宽高比 r1,…,rm 。如果以每个像素为中心时使用所有的大小与宽高比的组合，输入图像将一共得到 whnm 个锚框。虽然这些锚框可能覆盖了所有的真实边界框，但计算复杂度容易过高。因此，我们通常只对包含 s1 或 r1 的大小与宽高比的组合感兴趣，即

(s1,r1),(s1,r2),…,(s1,rm),(s2,r1),(s3,r1),…,(sn,r1).

也就是说，以相同像素为中心的锚框的数量为 n+m−1 。对于整个输入图像，我们将一共生成 wh(n+m−1) 个锚框。

以上生成锚框的方法已实现在MultiBoxPrior函数中。指定输入、一组大小和一组宽高比，该函数将返回输入的所有锚框。

5.交并比

我们刚刚提到某个锚框较好地覆盖了图像中的狗。如果该目标的真实边界框已知，这里的“较好”该如何量化呢？一种直观的方法是衡量锚框和真实边界框之间的相似度。我们知道，Jaccard系数（Jaccard index）可以衡量两个集合的相似度。给定集合 A 和 B ，它们的Jaccard系数即二者交集大小除以二者并集大小：

J(A,B)=|A∩B||A∪B|.

实际上，我们可以把边界框内的像素区域看成是像素的集合。如此一来，我们可以用两个边界框的像素集合的Jaccard系数衡量这两个边界框的相似度。当衡量两个边界框的相似度时，我们通常将Jaccard系数称为交并比（Intersection over Union，IoU），即两个边界框相交面积与相并面积之比，如图9.2所示。交并比的取值范围在0和1之间：0表示两个边界框无重合像素，1表示两个边界框相等。

6.标注训练集的锚框

在训练集中，我们将每个锚框视为一个训练样本。为了训练目标检测模型，我们需要为每个锚框标注两类标签：一是锚框所含目标的类别，简称类别；二是真实边界框相对锚框的偏移量，简称偏移量（offset）。在目标检测时，我们首先生成多个锚框，然后为每个锚框预测类别以及偏移量，接着根据预测的偏移量调整锚框位置从而得到预测边界框，最后筛选需要输出的预测边界框。

我们知道，在目标检测的训练集中，每个图像已标注了真实边界框的位置以及所含目标的类别。在生成锚框之后，我们主要依据与锚框相似的真实边界框的位置和类别信息为锚框标注。那么，该如何为锚框分配与其相似的真实边界框呢？

假设图像中锚框分别为 A1,A2,…,Ana ，真实边界框分别为 B1,B2,…,Bnb ，且 na≥nb 。定义矩阵 X∈Rna×nb ，其中第 i 行第 j 列的元素 xij 为锚框 Ai 与真实边界框 Bj 的交并比。 首先，我们找出矩阵 X 中最大元素，并将该元素的行索引与列索引分别记为 i1,j1 。我们为锚框 Ai1 分配真实边界框 Bj1 。显然，锚框 Ai1 和真实边界框 Bj1 在所有的“锚框—真实边界框”的配对中相似度最高。接下来，将矩阵 X 中第 i1 行和第 j1 列上的所有元素丢弃。找出矩阵 X 中剩余的最大元素，并将该元素的行索引与列索引分别记为 i2,j2 。我们为锚框 Ai2 分配真实边界框 Bj2 ，再将矩阵 X 中第 i2 行和第 j2 列上的所有元素丢弃。此时矩阵 X 中已有两行两列的元素被丢弃。 依此类推，直到矩阵 X 中所有 nb 列元素全部被丢弃。这个时候，我们已为 nb 个锚框各分配了一个真实边界框。 接下来，我们只遍历剩余的 na−nb 个锚框：给定其中的锚框 Ai ，根据矩阵 X 的第 i 行找到与 Ai 交并比最大的真实边界框 Bj ，且只有当该交并比大于预先设定的阈值时，才为锚框 Ai 分配真实边界框 Bj 。

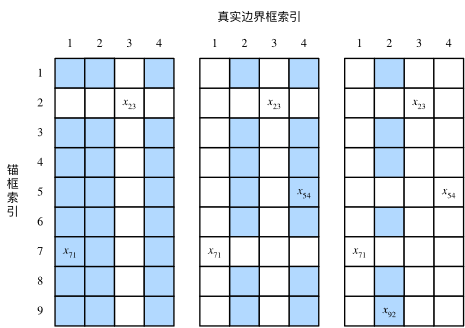
如图9.3（左）所示，假设矩阵 X 中最大值为 x23 ，我们将为锚框 A2 分配真实边界框 B3 。然后，丢弃矩阵中第2行和第3列的所有元素，找出剩余阴影部分的最大元素 x71 ，为锚框 A7 分配真实边界框 B1 。接着如图9.3（中）所示，丢弃矩阵中第7行和第1列的所有元素，找出剩余阴影部分的最大元素 x54 ，为锚框 A5 分配真实边界框 B4 。最后如图9.3（右）所示，丢弃矩阵中第5行和第4列的所有元素，找出剩余阴影部分的最大元素 x92 ，为锚框 A9 分配真实边界框 B2 。之后，我们只需遍历除去 A2,A5,A7,A9 的剩余锚框，并根据阈值判断是否为剩余锚框分配真实边界框。

现在我们可以标注锚框的类别和偏移量了。如果一个锚框 A 被分配了真实边界框 B ，将锚框 A 的类别设为 B 的类别，并根据 B 和 A 的中心坐标的相对位置以及两个框的相对大小为锚框 A 标注偏移量。由于数据集中各个框的位置和大小各异，因此这些相对位置和相对大小通常需要一些特殊变换，才能使偏移量的分布更均匀从而更容易拟合。设锚框 A 及其被分配的真实边界框 B 的中心坐标分别为 (xa,ya) 和 (xb,yb) ， A 和 B 的宽分别为 wa 和 wb ，高分别为 ha 和 hb ，一个常用的技巧是将 A 的偏移量标注为

其中常数的默认值为 μx=μy=μw=μh=0,σx=σy=0.1,σw=σh=0.2 。如果一个锚框没有被分配真实边界框，我们只需将该锚框的类别设为背景。类别为背景的锚框通常被称为负类锚框，其余则被称为正类锚框。

下面演示一个具体的例子。我们为读取的图像中的猫和狗定义真实边界框，其中第一个元素为类别（0为狗，1为猫），剩余4个元素分别为左上角的 x 和 y 轴坐标以及右下角的 x 和 y 轴坐标（值域在0到1之间）。这里通过左上角和右下角的坐标构造了5个需要标注的锚框，分别记为 A0,…,A4 （程序中索引从0开始）。先画出这些锚框与真实边界框在图像中的位置。

7.输出预测边界框

在模型预测阶段，我们先为图像生成多个锚框，并为这些锚框一一预测类别和偏移量。随后，我们根据锚框及其预测偏移量得到预测边界框。当锚框数量较多时，同一个目标上可能会输出较多相似的预测边界框。为了使结果更加简洁，我们可以移除相似的预测边界框。常用的方法叫作非极大值抑制（non-maximum suppression，NMS）。

我们来描述一下非极大值抑制的工作原理。对于一个预测边界框 B ，模型会计算各个类别的预测概率。设其中最大的预测概率为 p ，该概率所对应的类别即 B 的预测类别。我们也将 p 称为预测边界框 B 的置信度。在同一图像上，我们将预测类别非背景的预测边界框按置信度从高到低排序，得到列表 L 。从 L 中选取置信度最高的预测边界框 B1 作为基准，将所有与 B1 的交并比大于某阈值的非基准预测边界框从 L 中移除。这里的阈值是预先设定的超参数。此时， L 保留了置信度最高的预测边界框并移除了与其相似的其他预测边界框。 接下来，从 L 中选取置信度第二高的预测边界框 B2 作为基准，将所有与 B2 的交并比大于某阈值的非基准预测边界框从 L 中移除。重复这一过程，直到 L 中所有的预测边界框都曾作为基准。此时 L 中任意一对预测边界框的交并比都小于阈值。最终，输出列表 L 中的所有预测边界框。

小结

以每个像素为中心，生成多个大小和宽高比不同的锚框。
交并比是两个边界框相交面积与相并面积之比。
在训练集中，为每个锚框标注两类标签：一是锚框所含目标的类别；二是真实边界框相对锚框的偏移量。
预测时，可以使用非极大值抑制来移除相似的预测边界框，从而令结果简洁。

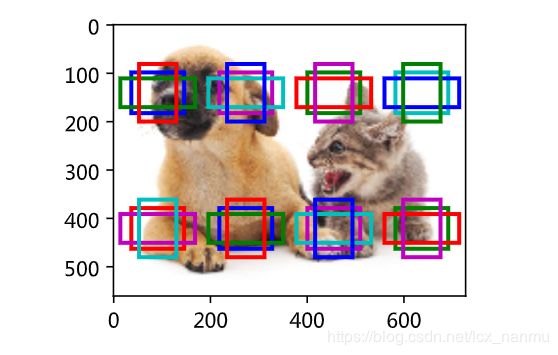
8.多尺度目标检测

以图像每个像素为中心都生成锚框，很容易生成过多锚框而造成计算量过大。举个例子，假设输入图像的高和宽分别为561像素和728像素，如果以每个像素为中心生成5个不同形状的锚框，那么一张图像上则需要标注并预测200多万个锚框（ 561×728×5 ）。

减少锚框个数并不难。一种简单的方法是在输入图像中均匀采样一小部分像素，并以采样的像素为中心生成锚框。此外，在不同尺度下，我们可以生成不同数量和不同大小的锚框。值得注意的是，较小目标比较大目标在图像上出现位置的可能性更多。举个简单的例子：形状为 1×1 、 1×2 和 2×2 的目标在形状为 2×2 的图像上可能出现的位置分别有4、2和1种。因此，当使用较小锚框来检测较小目标时，我们可以采样较多的区域；而当使用较大锚框来检测较大目标时，我们可以采样较少的区域。

为了演示如何多尺度生成锚框，我们先读取一张图像。它的高和宽分别为561像素和728像素。

w, h = img.size
w, h
d2l.set_figsize()

def display_anchors(fmap_w, fmap_h, s):
    # 前两维的取值不影响输出结果(原书这里是(1, 10, fmap_w, fmap_h), 我认为错了)
    fmap = torch.zeros((1, 10, fmap_h, fmap_w), dtype=torch.float32)
    
    # 平移所有锚框使均匀分布在图片上
    offset_x, offset_y = 1.0/fmap_w, 1.0/fmap_h
    anchors = d2l.MultiBoxPrior(fmap, sizes=s, ratios=[1, 2, 0.5]) + \
        torch.tensor([offset_x/2, offset_y/2, offset_x/2, offset_y/2])
    
    bbox_scale = torch.tensor([[w, h, w, h]], dtype=torch.float32)
    d2l.show_bboxes(d2l.plt.imshow(img).axes,
                    anchors[0] * bbox_scale)
display_anchors(fmap_w=4, fmap_h=2, s=[0.15])

display_anchors(fmap_w=2, fmap_h=1, s=[0.4])

display_anchors(fmap_w=1, fmap_h=1, s=[0.8])

二、图像风格迁移

1.样式迁移

如果你是一位摄影爱好者，也许接触过滤镜。它能改变照片的颜色样式，从而使风景照更加锐利或者令人像更加美白。但一个滤镜通常只能改变照片的某个方面。如果要照片达到理想中的样式，经常需要尝试大量不同的组合，其复杂程度不亚于模型调参。

在本节中，我们将介绍如何使用卷积神经网络自动将某图像中的样式应用在另一图像之上，即样式迁移（style transfer）[1]。这里我们需要两张输入图像，一张是内容图像，另一张是样式图像，我们将使用神经网络修改内容图像使其在样式上接近样式图像。图9.12中的内容图像为本书作者在西雅图郊区的雷尼尔山国家公园（Mount Rainier National Park）拍摄的风景照，而样式图像则是一副主题为秋天橡树的油画。最终输出的合成图像在保留了内容图像中物体主体形状的情况下应用了样式图像的油画笔触，同时也让整体颜色更加鲜艳。

2.方法

上图用一个例子来阐述基于卷积神经网络的样式迁移方法。首先，我们初始化合成图像，例如将其初始化成内容图像。该合成图像是样式迁移过程中唯一需要更新的变量，即样式迁移所需迭代的模型参数。然后，我们选择一个预训练的卷积神经网络来抽取图像的特征，其中的模型参数在训练中无须更新。深度卷积神经网络凭借多个层逐级抽取图像的特征。我们可以选择其中某些层的输出作为内容特征或样式特征。以图9.13为例，这里选取的预训练的神经网络含有3个卷积层，其中第二层输出图像的内容特征，而第一层和第三层的输出被作为图像的样式特征。接下来，我们通过正向传播（实线箭头方向）计算样式迁移的损失函数，并通过反向传播（虚线箭头方向）迭代模型参数，即不断更新合成图像。样式迁移常用的损失函数由3部分组成：内容损失（content loss）使合成图像与内容图像在内容特征上接近，样式损失（style loss）令合成图像与样式图像在样式特征上接近，而总变差损失（total variation loss）则有助于减少合成图像中的噪点。最后，当模型训练结束时，我们输出样式迁移的模型参数，即得到最终的合成图像。

3.小结

样式迁移常用的损失函数由3部分组成：内容损失使合成图像与内容图像在内容特征上接近，样式损失令合成图像与样式图像在样式特征上接近，而总变差损失则有助于减少合成图像中的噪点。
可以通过预训练的卷积神经网络来抽取图像的特征，并通过最小化损失函数来不断更新合成图像。
用格拉姆矩阵表达样式层输出的样式。