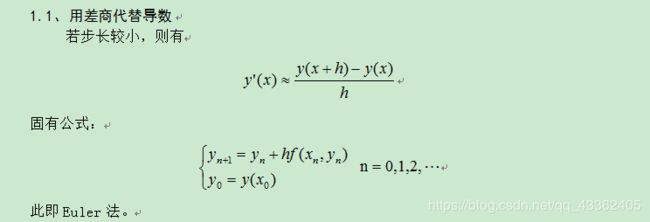matlab代码---常微分数值解的应用

MATLAB在常微分方程数值解中的应用

【摘 要】许多现实问题都可以通过微分方程的形式进行表示，传统解微分方程的方法有近似分析解法、表解法和图解法，这些方法需对其进行大量的假设，而使得数学模型有一定的失真，有一定的局限性。数值解法利用计算机，使得求解更精确、效率更高，而MATLAB是一种数学软件包，有高级编程格式，使得计算结果更具有可信性，因此微分方程的求解及MATLAB在其中的应用具有实际意义。本文对常微分方程数值解问题作进一步探讨，并应用MATLAB对其中难解的改进Euler法和Runge-Kutta法进行编程实现，程序简洁、直观，求解速度快、方法实用性较强。

【关 键 词】常微分方程 数值解 MATLAB Euler法 龙格-库塔方法 ode45 ode15s

Matlab in ordinary differential equation numerical solution of application
Yang Hua Zhang Lei
【Abstract】Many practical problems can be using differential equations in the form of representation, the traditional method of solving differential equations are similar analysis method, table method and graphical method, these methods to carry on the large amounts of hypothesis, so that the mathematical model has certain distortion, have certain limitation. Numerical solution of using a computer, make solving more accurate and more efficient, and MATLAB is a kind of mathematics software package, with advanced programming format, making calculation result is more credibility, therefore differential equation and solution of the MATLAB in one of the application of practical significance. This paper numerical solution of differential equation problem further discussion, and the application of MATLAB in which the difficult solution improvement Euler method and Runge - Kutta method on the programming, the program is concise, intuitive and solution speed, method of practical stronger.

【Key words】ordinary differential equation，numerical solution，Matlab，Euler method，Runge-Kutta method

【引 言】微分方程的概念：未知的函数以及它的某些阶的导数连同自变量都由一已知方程联系在一起的方程称为微分方程。如果未知函数是一元函数，称为常微分方程。常微分方程的一般形式为

微分方程是数学科学联系实际问题的主要桥梁之一，它是含有未知数及其导数的方程。常微分方程的求解是现代科学研究和工程技术中经常遇到的问题，然而，从实际问题中建立起来的微分方程往往具有非常复杂的形式，有写解析式难以计算，有的则根本不能用解析式来表达。在实际上对初值问题，一般是要求得到解在若干个点上满足规定精确度的近似值，或者得到一个满足精确度要求的便于计算的表达式，所以利用数值解法求解实际问题显得非常重要。

一阶常微分方程的初值，其一般形式为

在本文的讨论中，总假设函数f（x，y）连续，且关于y满足莱布尼兹条件，即存在常数L，使得

1、建立数值解法的一些途径

1.2、使用数值积分
对微分方程两边积分得
1.3．四阶Runge-Kutta法

2、利用matlab求解一阶常微分方程的初值解

3 根据数值解法的思想编程实现
MATLAB 中有几个专门用于求解常微分方程的函数,它们的设计思想基于Runge - Kutta方法,基本设计思想为：从改进的欧拉方法比欧拉方法精度高的缘由着手,如果在区间[ x1 , xi+1 ] 多取几个点的斜率值,然后求取平均值,则可以构造出精度更高的计算方法。 这些函数主要包括：ode45、ode23、ode15s、ode113、ode23s、ode23t、ode23tb. 其中最常用的是函数ode45,该函数采用变步长四阶五阶Runge - Kutta法求数值解,并采用自适应变步长的求解方法。ode23采用二阶三阶Runge - Kutta法求数值解,与ode45类似,只是精度低一些。ode15s用来求刚性方程组。
ode45函数的调用格式为:
[ tout, yout ] = ode45 ( ’yprime’, [ t0, tf ] , y0)
其中yprime是表示f ( t, y)的M文件名, t0表示自变量的初始值, tf表示自变量的终值, y0表示初始向量值. 输出向量tout表示节点( t0 ; t1 ; ⋯; tn ) ,输出矩阵yout表示数值。

（1）建立自定义函数
用edit命令建立自定义函数名为rossler. m, 内容为:
function dx = rossler ( t, x)
dx=[-x(2)-x(3);x(1)+0.2*x(2);0.2+(x(1)-5.7)*x(3)];
（2）调用对微分方程数值解ode45函数求解
用edit命令建立一个命令文件rossler1. m, 内容为：
>>x0=[0;0;0];
>>[t,y]=ode45(’rossler’,[0,100],x0); plot(t,y);
>>figure;
>>plot3(y(:,1),y(:,2),y(:,3))
得

（1）建立自定义函数
用edit命令建立自定义函数名为f.m,内容为:
function y =f(t,x)
y=[x(2);x(3);-t^2*x(2)*x(1)2-t*x(1)x(3)+exp(-tx(1))];
(2)调用对微分方程数值解ode45函数求解
用edit命令建立一个命令文件f2. m,内容为:

x0=[2;0;0];
[t,y] =ode45(’f’,[0,10],x0);plot(t,y);
figure;
plot3(y(:,1),y(:,2), y(:,3))
得

调用对微分方程数值解ode15s函数求解
>>x0=[2;0;0];
>>[t,y]=ode15s(’f’,[0,10],x0);plot(t,y(:,1))
>>figure;

plot(t,y(:,2))
得

x1 ( t) x2 ( t)

 用刚性方程求解函数可以快速求出该方程的数值解,并且画出两个状态变量的时间曲线。x1 ( t) 曲线变化比较平滑, x2 ( t) 曲线变化在某些点上较快.

参考文献:
【1】王高雄,等. 常微分方程(第3版)[M].北京:高等教育出版社, 2006.
【2】薛定宇,陈阳泉.高等应用数学问题的MATLAB求解[M].北京:清华大学出版社, 2004.
【3】李俐玲.关于数学问题的MATLAB实现方法[J].四川师范大学学报(自然科学版), 2003.
【4】陈怀琛, matlab及其在理工课程中的应用指南（第三版）.西安电子科技大学出版社.
【5】张得丰，matlab数值分析与应用（第二版）.国防工业出版社.
【6】杜挺松、沈艳军、覃太贵.数值分析及实验.科学出版社.