LSD_SLAM

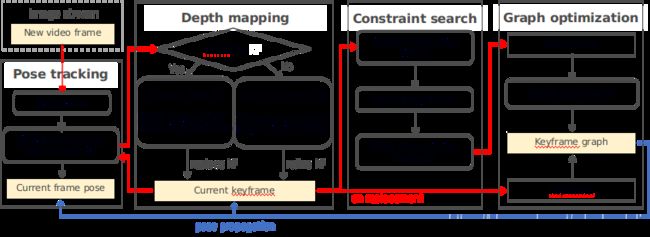
1. Overview

LSD SLAM 算法主要在以下两篇论文中提出：
[1] 2013 Semi-dense Visual Odometry for a Monocular Camera
[2] 2014 LSD-SLAM: Large-Scale Direct Monocular SLAM

三大模块

• Pose tracking： 当前帧与当前关键帧进行匹配得到当前帧的位姿，匹配方法为直接法;
• Depth mapping： 判断当前帧与当前关键帧距离是否大于一定阈值来决定是否将当前帧设为新的关键帧，
  若构建新的关键帧，则构建新的深度图;
  若不构建，则更新当前关键帧的深度图;
  这部分主要在论文[1]中详细展开。
• Graph optimization： 搜寻闭环约束，进行图优化.

2. Pose tracking

2.1 直接法

根据图像灰度信息，最小化光度误差（Photometric error），计算相机运动。可以不用计算关键点和描述子，既避免了特征的计算时间，也避免了特征缺失情况。但对光照比较敏感。

$P$为相机1坐标系下的三维坐标， $p_1$和$p_2$分别为$P$在相机1和相机2图像上的像素坐标。

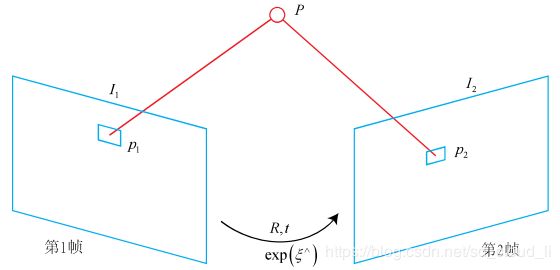
由三维空间坐标通过相机内参矩阵投影到像素坐标。
$$p_1=\left[\begin{array}{c}{u}_1\\ v_1\\ 1\end{array}\right]=\frac{1}{Z_1}KP,$$
$$p_2=\left[\begin{array}{c}{u}_2\\ v_2\\ 1\end{array}\right]=\frac{1}{Z_2}K(RP+t)=\frac{1}{Z_2}K(exp([\xi {]}_{\times })P{)}_{1:3}.$$

直接法中没有特征匹配，通过估计的变换寻找p1对应的p2使p1与p2的亮度误差最小：
$$mi{n}_{\xi }J(\xi )=\sum _{i=1}^N{e}_i^T{e}_i,e_i=I_1(p_1,i)-I_2(p_2,i).$$

2.2 LSD的直接法

使用方差归一化后的光度误差（variance-normalized photometric error）：
$$E_p({\xi }_{ji})=\sum _{\mathbf{p}\in {\Omega }_{D_i}}\Vert \frac{r_p^2(\mathbf{p},{\xi }_{ji})}{{\sigma }_{r_p(\mathbf{p},{\xi }_{ji})}^2}{\Vert }_{\delta }\text{\hspace{1em}(1)}$$
$$r_p(\mathbf{p},{\xi }_{ji}):=I_i(\mathbf{p})-I_j(\omega (\mathbf{p},D_i(\mathbf{p}),{\xi }_{ji}))\text{\hspace{1em}(2)}$$
$${\sigma }_{r_p(\mathbf{p},{\xi }_{ji})}^2:=2{\sigma }_I^2+(\frac{\partial r_p(\mathbf{p},{\xi }_{ji})}{\partial D_i(\mathbf{p})}{)}^2{V}_i(\mathbf{p})\text{\hspace{1em}(3)}$$

• ${\xi }_{ji}$为从关键帧$i$到当前帧$j$的SE3变换，用李代数形式表示;
• $\mathbf{p}$是在参考帧$I_i$观测到的有深度信息$(\mathbf{p}\in {\Omega }_{D_i})$的归一化图像点;
  $$\mathbf{p}=\left[\begin{array}{c}Xd\\ Yd\\ 1\end{array}\right].$$
  其中$d=\frac{1}{Z}$为深度的逆。
• $I:\Omega \to \mathbb{R}$ 每个像素坐标都对应一个光度值。
• $\omega$ 是一个投影映射将$\mathbf{p}$先通过${\xi }_{ji}$从$i$坐标系转到$j$坐标系，再通过相机内参矩阵投影至图像得到像素坐标。
• $D:\Omega \to \mathbb{R}$ 每个像素坐标对应一个逆深度， $V:\Omega \to \mathbb{R}$ 每个像素坐标对应逆深度的方差
• ${\sigma }_I^2$是图像的高斯噪声
• $\Vert \ast {\Vert }_{\delta }$为Huber-norm, 表示为：
  $$\Vert r^2{\Vert }_{\delta }:=\{\begin{array}{ll}\frac{r^2}{2\delta }& \text{if}|r|\le \delta \\ |r|-\frac{\delta }{2}& \text{otherwise}\end{array}$$

论文中在估计两帧间位姿变换的时候，把所有有逆深度假设的像素都用上了，但是每个逆深度的确定性不同，也就是有些逆深度比较准确有些不准确。准确与否体现在方差上，所以(1)用残差除以了方差，相当于给每对残差乘了个权重，方差大的则不准确权重小，方差小的较准确权重大。在论文中主要考虑两个方面的方差，一个是由逆深度估计不准确引入的，一个是由图像高斯噪声引起的。所以(3)式前面一项是两幅图像的高斯噪声，后一项为逆深度误差造成的不确定性：
$${\Sigma }_f=J_f{\Sigma }_x{J}_f^T$$

3. Depth mapping

LSD-SLAM构建的是半稠密逆深度地图（semi-dense inverse depth map），只对有明显梯度的像素位置进行深度估计，用逆深度表示，并且假设逆深度服从高斯分布。一旦一个图像帧被选为关键帧，则用其跟踪的参考帧的深度图对其进行深度图构建，之后跟踪到该新建关键帧的图像帧都会用来对其深度图进行更新。当然，追溯到第一帧，肯定是没有深度图的，因此第一帧的深度图是有明显梯度区域随机生成的深度。

这部分主要是用Tracking跟踪后的帧更新或构建深度图，分两种情况：

• 构建关键帧， 则构建新的深度图(Depth Map Creation);
• 不构建关键帧， 则更新当前关键帧的深度图(Depth Map Refinement).

3.1 Keyframe selection

论文中根据运动距离来确定，如果当前相机运动距离上一个关键帧达到一定阈值， 则把当前帧作为关键帧。并给出了距离函数：
$$dist({\xi }_{ji}):={\xi }_{ji}^T\mathbf{W}{\xi }_{ji}.$$

其中$\mathbf{W}$是一个对角矩阵包含权重。 为了防止尺度漂移带来的影响，作者统一将frame下的depth均值缩放到了1。这个时候阈值标准就一样了。

3.2 Depth Map Creation（Depth Map Propagation）

假设当前帧成为新的关键帧， 则将前一个关键帧的深度图投影到当前帧来初始化新关键帧的深度图。
将前一个关键帧的深度图传播到新关键帧的深度图时，主要考虑逆深度误差的传播。假设两帧之间的旋转很小，新关键帧的逆深度就可以近似为：
$$d_1(d_0)=(d_0^{-1}-t_z{)}^{-1}.$$
这里$t_z$是相机沿着光轴方向的位移， 在实际求逆深度的时候，是考虑旋转的，把参考关键帧上的点通过SE3变换到当前新的关键帧上来，然后求逆深度。逆深度的方差：
$${\sigma }_{d_1}^2=J_{d_1}{\sigma }_{d_0}^2{J}_{d_1}^T+{\sigma }_p^2=(\frac{d_1}{d_0}{)}^4{\sigma }_{d_0}^2+{\sigma }_p^2$$

这里${\sigma }_p^2$为预测不确定性。
传播完深度图和逆深度之后， 进行一次正则化(regularization)及异常值去除(outlier removal)。

• Regularization: 每个像素深度用周围像素对应的深度的加权平均来替代，这里权值为各自方差。若两个邻接像素的深度差值大于阈值$2\sigma$， 则不参与算平均。
• Outlier Removal: 在propagation过程中，如果光度发生明显的变化，或者绝对图像梯度低于一个阈值时，视为异常值。

3.3 Depth Map Refinement

假设当前帧不作为新的关键帧， 在Tracking线程对当前帧的位姿进行估计后，当前帧就被送到建图线程用于更新关键帧的深度图。论文中成为基于立体匹配的深度更新（Stereo-Based Depth Map Update）, 通过极线搜索在图像帧中找到与参考帧匹配的图像点，然后通过新匹配的观测点对逆深度进行更新。

3.3.1 参考图像帧选取

这部分主要讨论如何选取与当前帧做极线匹配是图像帧。

注意： 在论文和代码中都把与帧做立体匹配的图像帧称为参考帧(Reference Frame)。

考虑到准确性，立体匹配时尽可能选取视察和观测角小的两帧图像。当两帧图像间的基线过长，则会有很多错误匹配出现（大基线匹配点在图像上运动较大）。小基线的两个视图对深度进行估计误差往往比较大（小基线能恢复的深度范围就小）。因此，在论文中提出一种自适应的方法。

在论文中，把离当前帧远的图像帧称为“老的”， 那些最近获取的图像帧称为“新的”。 使用观察到像素的最老帧，其中视差搜索范围和观察角度不超过某个阈值。如下图所示， 左上是当前帧， 下面两行是之前的图像帧， 下面是距离当前帧的时间，负的越多就说明该帧越老。

使用观察到像素的最老帧，其中视差搜索范围和观察角度不超过某个阈值。如果视差搜索不成功（即未找到良好匹配），则像素的“年龄”会增加，这样后续的视差搜索将使用像素可能仍然可见的较新帧。

3.3.2 立体匹配策略

上一步已经选取好了待匹配的参考帧， 这部分主要介绍找到当前帧需要更新深度深度的像素点的对应点，在选定的参考帧中，对像素沿极线的强度进行了详尽的搜索，然后对匹配视差进行亚像素精确定位。基线，极线如下所示。

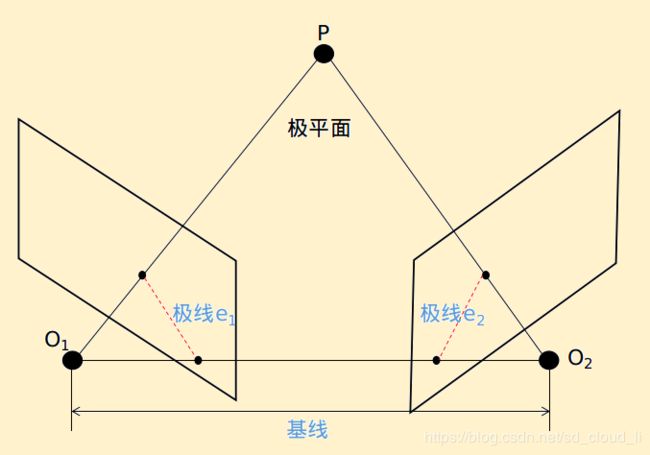
假设$I_2$为当前帧, 对于$\mathbf{p}$在$I_2$上的像素点， 我们在$I_1$上所对应的极线上搜索找对应点。
如果当前帧上的点已有逆深度的先验假设$N(d,{\sigma }_d^2)$, 则设置的逆深度搜索范围为$d\pm 2{\sigma }_d$， 否则在整个范围内搜索。

论文中在极线的五个等距点上使用SSD（Sum of Squared Distance）误差：虽然这显著提高了高频率图像区域的鲁棒性，但它不会改变这种搜索的纯一维性质。此外，它的计算效率很高，因为5个插值图像值中的4个可用于每个SSD评估。
$$E_{SSD}(u)=\sum _i[I_1(x_i+u)-I_0(x_i){]}^2$$

3.3.3 不确定性估计

通过立体匹配找到参考帧上的对应点后，我们可以求得新的逆深度值。 此外，我们还需要求解逆深度的不确定性。通过对两图像$I_0$, $I_1$立体匹配求得的最佳匹配点对应的逆深度可以表示为：
$$d^{\ast }=d(I_0,I_1,\xi ,\pi )$$
这里$\xi$为两帧间位姿变换， $\pi$为相机投影模型参数。 从而得到$d^{\ast }$的误差方差(error-variance)为：
$${\sigma }_d=J_d\Sigma J_d^T$$
这里$J_d$是对$d$的雅克比，$\Sigma$为输入误差的方差。

计算逆深度主要分为3个步骤：

1. 计算在参考帧中的对极线;
2. 在对极线上找到最好的匹配位置${\lambda }^{\ast }\in \mathbb{R}$(视差);
3. 通过${\lambda }^{\ast }$求出逆深度$d^{\ast }$。

这三个步骤分别涉及三个误差：

• 几何视差误差: $\xi$ 和$\pi$中的噪声将影响第1步极线的位置， 从而导致匹配点位置的误差;
• 光度视差误差： 在图像$I_0$和$I_1$上的噪声将影响第2步匹配位置的求取;
• 逆深度计算误差: 逆深度误差主要来源于两个地方， 一是匹配的像素位置， 另外就是两个图像间的基线长度。

接下来将对这几个误差如何建模进行分析。

a. 几何视差误差（Geometric disparity error）

理论上可以计算准确的$\xi$和$\pi$中噪声的方差， 但是在论文中指出这样计算增加计算的复杂度但没有等价地提升准确性， 因此论文中使用了一个简单的近似。 定义极线段：
$$L:=\left\{\begin{array}{c}{l}_0+\lambda \left(\begin{array}{c}{l}_x\\ l_y\end{array}\right)\mid \lambda \in S\end{array}\right\}$$
这里$\lambda$是在搜索范围内的视差， $(l_x,l_y{)}^T$是归一化的极线方向， $l_0$是极线上对应无穷远点的图像点， 假设$I_0$受到各向同性高斯噪声${ϵ}_l$的影响。 论文指出， 当搜索的极线段比较小， 并且旋转误差较小的情况下， 这个近似还是比较好的。

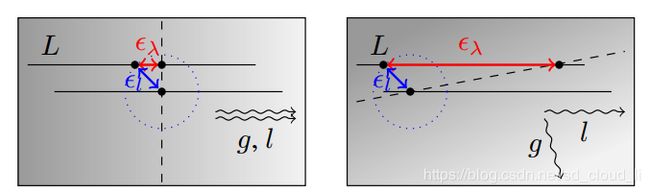
如图所示， L是极线段， $g,l$分别是梯度方向和极线方向， 圆中心的点是一个真值， 由于各向同性高斯噪声， 使得极线段有一个绝对偏差${ϵ}_l$, 最后再通过灰度等值线（即黑色虚线）找到灰度相同的点， 就得到了这个点和真值点之间的几何误差${ϵ}_{\lambda }$， 可以看出如果极线与图像梯度平行，则极线上的定位误差${ϵ}_l$会导致较小的视差误差${ϵ}_{\lambda }$，否则会导致较大的视差误差。

假设梯度局部不变， 则有：
$$l_0+\lambda \left(\begin{array}{c}{l}_x\\ l_y\end{array}\right)\stackrel{!}{＝}{g}_0+\gamma \left(\begin{array}{c}-g_y\\ g_x\end{array}\right)\gamma \in \mathbb{R}$$

这里$g_0$为等值线上的一点，$g_0$处的灰度值等于或接近待匹配像素的灰度值。$g:=(g_x,g_y)$表示归一化梯度方向向量，则(−gy,gx)T表示归一化等值线方向向量。 则$(-g_y,g_x{)}^T$表示归一化等值线方向向量。 故等式左边是沿极线搜索到的匹配点坐标， 等式右边表示该点位于等值线上。 由于下面会分析图像噪声的影响，所以这里假设$g_0$和$g$不受噪声影响。 等式两边同时与$g$进行內积， 得：
$${\lambda }^{\ast }(l_0)=\frac{⟨g,g_0-l_0⟩}{⟨g,l⟩}\text{\hspace{1em}(4)}$$
由协方差传播可得：
$${\sigma }_{\lambda (\xi ,\pi )}^2=J_{{\lambda }^{\ast }(l_0)}\left(\begin{array}{cc}{\sigma }_l^2& 0\\ 0& {\sigma }_l^2\end{array}\right)J_{{\lambda }^{\ast }(l_0)}^T\text{\hspace{1em}(5)}$$

由式(4)得：
$$J_{{\lambda }^{\ast }(l_0)}=\frac{\partial {\lambda }^{\ast }(l_0)}{\partial l_0}=-\frac{g^T}{⟨g,l⟩}$$
代人式(5)得：
$${\sigma }_{\lambda (\xi ,\pi )}^2=\frac{⟨g,g⟩\cdot {\sigma }_l^2}{⟨g,l{⟩}^2}=\frac{{\sigma }_l^2}{⟨g,l{⟩}^2}\text{\hspace{1em}(6)}$$
其中， ${\sigma }_l^2$为极线位置误差${ϵ}_l$的方差， 只和相机位姿$\xi$和相机参数$\pi$相关。

从式(6)可以得出以下结论:

• 位姿扰动造成的${\sigma }_l^2$越大， 则几何视差误差越大
• 梯度$g$和极线$l$夹角越小， 几何视差误差越小

b. 光度视差误差

在极线搜索的时候，我们找到的点满足SSD误差最小， 也就有：
$${\lambda }^{\ast }＝\underset{\lambda }{\min }(i_{ref}-I_p(\lambda ){)}^2\text{\hspace{1em}(7)}$$

这里的$i_{ref}$是当前帧的灰度， $I_p(\lambda )$是参考帧图像极线在视差为$\lambda$位置的灰度。 假设在极线上有过彻底的搜索， 得到一个很好的初始位置${\lambda }_0$, 对式(7)中的$I_p(\lambda )$做一阶泰勒展开， 然后对增量$\Delta \lambda$求导并令式子等于0， 则可解出
$${\lambda }^{\ast }(I)={\lambda }_0+\Delta \lambda ={\lambda }_0+(i_{ref}-I_p({\lambda }_0))g_p^{-1}\text{\hspace{1em}(8)}$$
这里的$g_p$是图像沿极线的梯度。 这里同样不考虑梯度的噪声， 只考虑两个图像的噪声。 有：

$${\sigma }_{\lambda (I)}^2=J_{{\lambda }^{\ast }(I)}\left(\begin{array}{cc}{\sigma }_i^2& 0\\ 0& {\sigma }_i^2\end{array}\right)J_{{\lambda }^{\ast }(I)}^T=\frac{2{\sigma }_i^2}{g_p^2}\text{\hspace{1em}(9)}$$

这里由于同时对关键帧和参考帧的灰度都计算了噪声，因此会有２这个系数，这个方程是一个线性方程，我们也可以这么求：
$${\sigma }_{\lambda (I)}^2=\text{Var}({\lambda }^{\ast }(I))=(\text{Var}(i_{ref})+\text{Var}(I_p))g_p^{-2}=\frac{2{\sigma }_i^2}{g_p^2}$$
这里的${\sigma }_i^2$是图像的高斯噪声的方差，这里的光度视差误差和几何光度误差是独立的。
$$

这里的${\sigma }_i^2$是图像的高斯噪声的方差，这里的光度视差误差和几何光度误差是独立的。

如下图所示，比较直观。直线斜率的绝对值表示极线上梯度大小，当梯度值越大时，可以看出光度视差误差越小。直接法因为是靠图像梯度来不断调整位姿的，因此梯度必须较大，这样才能在优化中较快较好地收敛。

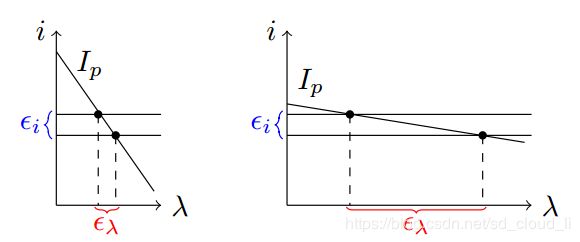
结合上述代数和几何分析，得出结论：

• 图像噪声越大，光度视差误差越大
• 极线方向上梯度越大，光度视差误差越小

c. 逆深度计算误差

论文中指出，当旋转比较小的时候， 逆深度$d$和视差$\lambda$近似成一个比例关系（当旋转较小时可近似为一个双目模型， 视差$\lambda =u_L-u_R=\frac{fb}{z}$）, 而$\lambda$误差方差可以表现为几何视差误差和光度视差误差方差之和：

$${\sigma }_{d,\text{obs}}^2={\alpha }^2\left(\begin{array}{c}{\sigma }_{\lambda (\xi ,\pi )}^2+{\sigma }_{\lambda (I)}^2\end{array}\right)\text{\hspace{1em}(10)}$$
其中$\alpha$是权重， 其定义如下：

$$\alpha :=\frac{\delta d}{\delta \lambda }\text{\hspace{1em}(11)}$$

式中，$\delta d$为搜索反深度间隔的长度，$\delta \lambda$为搜索极外线段的长度。虽然$\alpha$在相机平移长度上是反线性的，但它也取决于平移方向和像素在图像中的位置(这句没看懂)。
如果一个小的极线上的变化会导致深度变化大， 那就是说此时不确定性大，故权重大一些。

考虑到在极线上搜索匹配点的时候，是使用了多个点，因此实际上这里是给出了逆深度误差的上限：
$${\sigma }_{d,\text{obs}}^2\le {\alpha }^2\left(\begin{array}{c}\text{min}\{{\sigma }_{\lambda (\xi ,\pi )}^2\}+\text{min}\{{\sigma }_{\lambda (I)}^2\}\end{array}\right)\text{\hspace{1em}(12)}$$

3.3.4 深度观测融合

通过当前帧匹配的像素为深度提供一个新的观测值，然后就可以把当前观测的深度融合到关键帧的深度地图中去。这里有两种情况：当对应像素点没有深度先验时则由新的观测值构建新的先验；当已经有先验值的话，则把新观测值融合到先验中去。在这个融合的过程，使用了两个高斯分布乘法的方式：对于给定先验$\mathcal{N}(d_p,{\sigma }_p^2)$以及有噪声的观测值$\mathcal{N}(d_o,{\sigma }_o^2)$，给出后验估计：

$$\mathcal{N}\left(\begin{array}{c}\frac{{\sigma }_p^2{d}_o+{\sigma }_o^2{d}_p}{{\sigma }_p^2+{\sigma }_o^2},\frac{{\sigma }_p^2{\sigma }_o^2}{{\sigma }_p^2+{\sigma }_o^2}\end{array}\right)\text{\hspace{1em}(13)}$$

4. Map Optimization

这部分在论文中叫做一致性约束（constraint acquisition）， 是算法的核心（解决尺度问题）， 因为长距离会出现尺度漂移， 这部分主要分为闭环检测和全局优化。 检测闭环的方式是帧与帧之间做双向跟踪， 删选好候选帧就添加到pose graph中， 进行图优化。

关于选择候选帧，主要步骤：

• 视角和距离判别
• SE3跟踪检测
• Sim3跟踪检测

第一个步骤是根据每个关键帧求得的位姿判断的， 把距离当前关键帧较远的关键帧剔除。 第二步是通过SE3跟踪选取与当前关键帧距离较近的候选关键帧。 第三步是核心， 把每一个候选帧都与当前关键帧做双向的Sim3跟踪， 如果都成功， 并且两个$\mathfrak{s}\mathfrak{i}\mathfrak{m}(3)$的马氏距离足够小，则任务是闭环，并向pose graph中添加边。

接下来主要看一下Sim(3)求解以及双向跟踪检测(reciprocal tracking check).

4.1 Sim3求解

4.1.1 原理分析

a. Sim3 图像对齐

首先和$\mathfrak{s}\mathfrak{e}(3)$变换一样， 对于两帧图像上对应归一化图像点$p^{\prime }$和$p$通过$\mathfrak{s}\mathfrak{i}\mathfrak{m}(3)$变换有：
$$\underset{{\omega }_n}{{\mathbf{p}}^{\prime }=\left(\begin{array}{c}{x}^{\prime }/z^{\prime }\\ y^{\prime }/z^{\prime }\\ 1\end{array}\right)}\text{with}\underset{w_s}{\left(\begin{array}{c}{x}^{\prime }\\ y^{\prime }\\ z^{\prime }\\ 1\end{array}\right):={\text{exp}}_{\mathfrak{s}\mathfrak{i}\mathfrak{m}(3)}(\xi )\left(\begin{array}{c}{\mathbf{p}}_x/d\\ {\mathbf{p}}_y/d\\ 1/d\\ 1\end{array}\right)}\text{\hspace{1em}(14)}$$

上式的代价函数和SE(3)相比多了一项尺度项， 并且依旧使用归一化方差：
$$E({\xi }_{ji})=\sum _{\mathbf{p}\in {\Omega }_{D_i}}\Vert \frac{r_p^2(\mathbf{p},{\xi }_{ji})}{{\sigma }_{r_p(\mathbf{p},{\xi }_{ji})}^2}+\frac{r_d^2(\mathbf{p},{\xi }_{ji})}{{\sigma }_{r_d(\mathbf{p},{\xi }_{ji})}^2}{\Vert }_{\delta }\text{\hspace{1em}(15)}$$

这里的光度残差和方差的定义和SE3跟踪是一样的:
$$r_p(\mathbf{p},{\xi }_{ji}):=I_i(\mathbf{p})-I_j(\omega (\mathbf{p},D_i(\mathbf{p}),{\xi }_{ji}))\text{\hspace{1em}(16)}$$

$${\sigma }_{r_p(\mathbf{p},{\xi }_{ji})}^2:=2{\sigma }_I^2+(\frac{\partial r_p(\mathbf{p},{\xi }_{ji})}{\partial D_i(\mathbf{p})}{)}^2{V}_i(\mathbf{p})\text{\hspace{1em}(17)}$$

以及深度残差和方差定义如下：
$$r_d(\mathbf{p},{\xi }_{ji})=[{\mathbf{p}}^{\prime }{]}_3-D_j([{\mathbf{p}}^{\prime }{]}_{1,2})\text{\hspace{1em}(18)}$$

$${\sigma }_{r_d(\mathbf{p},{\xi }_{ji})}^2=V_j([{\mathbf{p}}^{\prime }{]}_{1,2})\left(\begin{array}{c}\frac{\partial r_d(\mathbf{p},{\xi }_{ji})}{\partial D_j([{\mathbf{p}}^{\prime }{]}_{1,2})}\end{array}\right)+V_i(\mathbf{p})\left(\begin{array}{c}\frac{\partial r_d(\mathbf{p},{\xi }_{ji})}{\partial D_i(\mathbf{p})}\end{array}\right)\text{\hspace{1em}(19)}$$

这里${\mathbf{p}}^{\prime }:={\omega }_s((p),D_i(\mathbf{p}),{\xi }_{ji})$， 其中$w_s$是用了sim3的变换。

求解部分用迭代变权重高斯牛顿算法，关于雅克闭矩阵的推导以后再推。

4.2 双向跟踪检测

由于论文中采用的是直接法，虽然代码中有fabmap检测闭环的部分，但是其默认检测闭环的方式是帧与帧之间做双向跟踪（Reciprocal tracking check）。首先搜索最近的10个关键帧及一些外观较像的帧作为候选帧，对每一个候选帧都计算其与当前关键帧彼此跟踪的???(3)，然后计算两者间的马氏距离的平方：
$$e\left({\xi }_{j_{k}i},{\xi }_{i{j}_k}\right):={\left({\xi }_{j_{k}i}\circ {\xi }_{i{j}_k}\right)}^T{\left({\mathbf{\Sigma }}_{j_{k}i}+{\text{Adj}}_{j_{k}i}{\mathbf{\Sigma }}_{i{j}_k}{\text{Adj}}_{j_{k}i}^T\right)}^{-1}\left({\xi }_{j_{k}i}\circ {\xi }_{i{j}_k}\right)\text{\hspace{1em}(20)}$$

当距离足够小时表明相似度较高，就将这一帧插入全局地图中。最后执行图优化（g2o中的pose graph optimization），边为连接关系，节点为关键帧，即优化：
$$E({\xi }_{W1}\cdots {\xi }_{Wn})=\sum _{({\xi }_{ji},\Sigma )\in \epsilon }({\xi }_{ji}\circ {\xi }_{Wi}^{-1}\circ {\xi }_{Wj}{)}^T{\Sigma }_{ji}^{-1}({\xi }_{ji}\circ {\xi }_{Wi}^{-1}\circ {\xi }_{Wj})\text{\hspace{1em}(21)}$$

参考

• LSDSLAM算法解析
• LSD-SLAM笔记之SE3Tracking
• LSD-SLAM笔记之DepthMap
• LSD-SLAM笔记之一致性约束
• SVO & LSD_SLAM(贺一家)视频
• SLAM 14讲