KNN算法-学习笔记整理

机器学习算法

机器学习算法是一类从数据中自动分析获得规律（模型），并利用规律对未知数据进行预测的算法

开发机器学习应用程序的步骤

• 收集数据
  可以使用很多方法收集样本数据，如：制作网络爬虫从网站上抽取数据、从RSS反馈或者API中得到信息、设备发送过来的实测数据。
• 准备输入数据
  得到数据之后，还必须确保数据格式符合要求。
• 分析输入数据
  这一步的主要作用是确保数据集中没有垃圾数据。如果是使用信任的数据来源，那么可以直接跳过这个步骤
• 训练算法
  机器学习算法从这一步才真正开始学习。如果使用无监督学习算法，由于不存在目标变量值，故而也不需要训练算法，所有与算法相关的内容在第（5）步
• 测试算法
  这一步将实际使用第（4）步机器学习得到的知识信息。当然在这也需要评估结果的准确率，然后根据需要重新训练你的算法
• 使用算法
  转化为应用程序，执行实际任务。以检验上述步骤是否可以在实际环境中正常工作。如果碰到新的数据问题，同样需要重复执行上述的步骤

环境准备

Scikit-learn是一个基于python的机器学习库，封装了大量经典以及最新的机器学习模型。

pip3 install Scikit-learn

注：安装scikit-learn需要Numpy, Scipy等库

Scikit-learn包含的内容

数据的类型

按照机器学习的数据分类可以将数据分成：

• 标称型：标称型目标变量的结果只在有限目标集中取值，如真与假(标称型目标变量主要用于分类)
• 数值型：数值型目标变量则可以从无限的数值集合中取值，如0.100，42.001等 (数值型目标变量主要用于回归分析)

按照数据的本身分布特性

• 离散型
  • 离散变量是指其数值只能用自然数或整数单位计算的则为离散变量
• 连续型
  • 连续型数据是指在指定区间内可以是任意一个数值,存在一定规律

数据的特征工程

从数据中抽取出来的对预测结果有用的信息，通过专业的技巧进行数据处理，是的特征能在机器学习算法中发挥更好的作用。优质的特征往往描述了数据的固有结构。 最初的原始特征数据集可能太大，或者信息冗余，因此在机器学习的应用中，一个初始步骤就是选择特征的子集，或构建一套新的特征集，减少功能来促进算法的学习，提高泛化能力和可解释性。

特征工程的意义

• 更好的特征意味着更强的鲁棒性
• 更好的特征意味着只需用简单模型
• 更好的特征意味着更好的结果

特征工程之特征处理

特征工程中最重要的一个环节就是特征处理，特征处理包含了很多具体的专业技巧
特征预处理

• 单个特征
  • 归一化
  • 标准化
  • 缺失值
• 多个特征
  • 降维
    • PCA
      特征工程之特征抽取与特征选择
      如果说特征处理其实就是在对已有的数据进行运算达到目标的数据标准。特征抽取则是将任意数据格式（例如文本和图像）转换为机器学习的数字特征。而特征选择是在已有的特征中选择更好的特征。

特征抽取

现实世界中多数特征都不是连续变量，比如分类、文字、图像等，为了对非连续变量做特征表述，需要对这些特征做数学化表述，因此就用到了特征提取. sklearn.feature_extraction提供了特征提取的很多方法

分类特征变量提取

sklearn.feature_extraction.DictVectorizer(sparse = True)
将映射列表转换为Numpy数组或scipy.sparse矩阵

• sparse 是否转换为scipy.sparse矩阵表示，默认开启

方法
fit_transform(X,y)
应用并转化映射列表X，y为目标类型
inverse_transform(X[, dict_type])
将Numpy数组或scipy.sparse矩阵转换为映射列表

from sklearn.feature_extraction import DictVectorizer
onehot = DictVectorizer() # 如果结果不用toarray，请开启sparse=False
instances = [{'city': '北京','temperature':100},{'city': '上海','temperature':60}, {'city': '深圳','temperature':30}]
X = onehot.fit_transform(instances).toarray()
print(onehot.inverse_transform(X))

文本特征提取（只限于英文）

文本的特征提取应用于很多方面，比如说文档分类、垃圾邮件分类和新闻分类。那么文本分类是通过词是否存在、以及词的概率（重要性）来表示。

文档的中词的出现

数值为1表示词表中的这个词出现，为0表示未出现

sklearn.feature_extraction.text.CountVectorizer()

将文本文档的集合转换为计数矩阵（scipy.sparse matrices）
方法
fit_transform(raw_documents,y)
学习词汇词典并返回词汇文档矩阵

from sklearn.feature_extraction.text import CountVectorizer
content = ["life is short,i like python","life is too long,i dislike python"]
vectorizer = CountVectorizer()
print(vectorizer.fit_transform(content).toarray())

需要toarray()方法转变为numpy的数组形式
温馨提示：每个文档中的词，只是整个语料库中所有词，的很小的一部分，这样造成特征向量的稀疏性（很多值为0）为了解决存储和运算速度的问题，使用Python的scipy.sparse矩阵结构

TF-IDF表示词的重要性

class sklearn.feature_extraction.text.TfidfVectorizer()

方法
fit_transform(raw_documents,y)
学习词汇和idf，返回术语文档矩阵。

from sklearn.feature_extraction.text import TfidfVectorizer
content = ["life is short,i like python","life is too long,i dislike python"]
vectorizer = TfidfVectorizer(stop_words='english')
print(vectorizer.fit_transform(content).toarray())
print(vectorizer.vocabulary_)

特征预处理

单个特征

• 归一化
  归一化首先在特征（维度）非常多的时候，可以防止某一维或某几维对数据影响过大，也是为了把不同来源的数据统一到一个参考区间下，这样比较起来才有意义，其次可以程序可以运行更快。
  常用的方法是通过对原始数据进行线性变换把数据映射到[0,1]之间，变换的函数为：
  
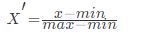
  其中min是样本中最小值，max是样本中最大值，注意在数据流场景下最大值最小值是变化的，另外，最大值与最小值非常容易受异常点影响，所以这种方法鲁棒性较差，只适合传统精确小数据场景。
• 标准化
  常用的方法是z-score标准化，经过处理后的数据均值为0，标准差为1，处理方法是：
  
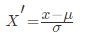
  其中μ是样本的均值，σ是样本的标准差，它们可以通过现有的样本进行估计，在已有的样本足够多的情况下比较稳定，适合嘈杂的数据场景
  sklearn中提供了StandardScalar类实现列标准化:

In [2]: import numpy as np

In [3]: X_train = np.array([[ 1., -1.,  2.],[ 2.,  0.,  0.],[ 0.,  1., -1.]])

In [4]: from sklearn.preprocessing import StandardScaler

In [5]: std = StandardScaler()

In [6]: X_train_std = std.fit_transform(X_train)

In [7]: X_train_std
Out[7]:
array([[ 0.        , -1.22474487,  1.33630621],
       [ 1.22474487,  0.        , -0.26726124],
       [-1.22474487,  1.22474487, -1.06904497]])

• 缺失值
  由于各种原因，许多现实世界的数据集包含缺少的值，通常编码为空白，NaN或其他占位符。然而，这样的数据集与scikit的分类器不兼容，它们假设数组中的所有值都是数字，并且都具有和保持含义。使用不完整数据集的基本策略是丢弃包含缺失值的整个行或列。然而，这是以丢失可能是有价值的数据（即使不完整）的代价。更好的策略是估算缺失值，即从已知部分的数据中推断它们。
  填充缺失值 使用sklearn.preprocessing中的Imputer类进行数据的填充

class Imputer(sklearn.base.BaseEstimator, sklearn.base.TransformerMixin)
    """
    用于完成缺失值的补充

    :param param missing_values: integer or "NaN", optional (default="NaN")
        丢失值的占位符，对于编码为np.nan的缺失值，使用字符串值“NaN”

    :param strategy: string, optional (default="mean")
        插补策略
        如果是“平均值”，则使用沿轴的平均值替换缺失值
        如果为“中位数”，则使用沿轴的中位数替换缺失值
        如果“most_frequent”，则使用沿轴最频繁的值替换缺失

    :param axis: integer, optional (default=0)
        插补的轴
        如果axis = 0，则沿列排列
        如果axis = 1，则沿行排列
    """

>>> import numpy as np
>>> from sklearn.preprocessing import Imputer
>>> imp = Imputer(missing_values='NaN', strategy='mean', axis=0)
>>> imp.fit([[1, 2], [np.nan, 3], [7, 6]])
Imputer(axis=0, copy=True, missing_values='NaN', strategy='mean', verbose=0)
>>> X = [[np.nan, 2], [6, np.nan], [7, 6]]
>>> print(imp.transform(X))                          
[[ 4.          2.        ]
 [ 6.          3.666...]
 [ 7.          6.        ]]

多个特征

降维
PCA（Principal component analysis），主成分分析。特点是保存数据集中对方差影响最大的那些特征，PCA极其容易受到数据中特征范围影响，所以在运用PCA前一定要做特征标准化，这样才能保证每维度特征的重要性等同。
sklearn.decomposition.PCA

class PCA(sklearn.decomposition.base)
   """
   主成成分分析

   :param n_components: int, float, None or string
       这个参数可以帮我们指定希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目，此时n_components是一个大于1的整数。
       我们也可以用默认值，即不输入n_components，此时n_components=min(样本数，特征数)

   :param whiten: bool, optional (default False)
      判断是否进行白化。所谓白化，就是对降维后的数据的每个特征进行归一化。对于PCA降维本身来说一般不需要白化,如果你PCA降维后有后续的数据处理动作，可以考虑白化，默认值是False，即不进行白化

   :param svd_solver:
      选择一个合适的SVD算法来降维,一般来说，使用默认值就够了。
    """

>>> import numpy as np
>>> from sklearn.decomposition import PCA
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> pca = PCA(n_components=2)
>>> pca.fit(X)
PCA(copy=True, iterated_power='auto', n_components=2, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)
>>> print(pca.explained_variance_ratio_)
[ 0.99244...  0.00755...]

特征选择

降维本质上是从一个维度空间映射到另一个维度空间，特征的多少别没有减少，当然在映射的过程中特征值也会相应的变化。举个例子，现在的特征是1000维，想要把它降到500维。降维的过程就是找个一个从1000维映射到500维的映射关系。原始数据中的1000个特征，每一个都对应着降维后的500维空间中的一个值。假设原始特征中有个特征的值是9，那么降维后对应的值可能是3。而对于特征选择来说，有很多方法：

• Filter(过滤式):VarianceThreshold
• Embedded(嵌入式)：正则化、决策树
• Wrapper(包裹式)
• 其中过滤式的特征选择后，数据本身不变，而数据的维度减少。而嵌入式的特征选择方法也会改变数据的值，维度也改变。Embedded方式是一种自动学习的特征选择方法，后面讲到具体的方法的时候就能理解了。
  特征选择主要有两个功能：
  • 减少特征数量，降维，使模型泛化能力更强，减少过拟合
  • 增强特征和特征值之间的理解

sklearn.feature_selection
去掉取值变化小的特征（删除低方差特征）
VarianceThreshold 是特征选择中的一项基本方法。它会移除所有方差不满足阈值的特征。默认设置下，它将移除所有方差为0的特征，即那些在所有样本中数值完全相同的特征。
假设我们要移除那些超过80%的数据都为1或0的特征

from sklearn.feature_selection import VarianceThreshold
X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
sel.fit_transform(X)
array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

scikit-learn数据集

• datasets.load_*()
  获取小规模数据集，数据包含在datasets里
• datasets.fetch_*()
  获取大规模数据集，需要从网络上下载，函数的第一个参数是data_home，表示数据集下载的目录，默认是 ~/scikit_learn_data/，要修改默认目录，可以修改环境变量SCIKIT_LEARN_DATA
• datasets.make_*()
  本地生成数据集

load和 fetch 函数返回的数据类型是 datasets.base.Bunch，本质上是一个 dict，它的键值对可用通过对象的属性方式访问。主要包含以下属性：

• data：特征数据数组，是 n_samples * n_features 的二维 numpy.ndarray 数组
• target：标签数组，是 n_samples 的一维 numpy.ndarray 数组
• DESCR：数据描述
• feature_names：特征名
• target_names：标签名

数据集目录可以通过datasets.get_data_home()获取，clear_data_home(data_home=None)删除所有下载数据

• datasets.get_data_home(data_home=None)
  返回scikit学习数据目录的路径。这个文件夹被一些大的数据集装载器使用，以避免下载数据。默认情况下，数据目录设置为用户主文件夹中名为“scikit_learn_data”的文件夹。或者，可以通过“SCIKIT_LEARN_DATA”环境变量或通过给出显式的文件夹路径以编程方式设置它。’〜'符号扩展到用户主文件夹。如果文件夹不存在，则会自动创建。
• sklearn.datasets.clear_data_home(data_home=None)
  删除存储目录中的数据

获取本地生成数据

生成本地分类数据：

• sklearn.datasets.make_classification

class make_classification(n_samples=100, n_features=20, n_informative=2, n_redundant=2, n_repeated=0, n_classes=2, n_clusters_per_class=2, weights=None, flip_y=0.01, class_sep=1.0, hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=None)
"""
生成用于分类的数据集

:param n_samples:int，optional（default = 100)，样本数量

:param n_features:int，可选（默认= 20），特征总数

:param n_classes:int，可选（default = 2),类（或标签）的分类问题的数量

:param random_state:int，RandomState实例或无，可选（默认=无）
  如果int，random_state是随机数生成器使用的种子; 如果RandomState的实例，random_state是随机数生成器; 如果没有，随机数生成器所使用的RandomState实例np.random

:return :X,特征数据集；y,目标分类值
"""

from sklearn.datasets.samples_generator import make_classification
X,y= datasets.make_classification(n_samples=100000, n_features=20,n_informative=2, n_redundant=10,random_state=42)

生成本地回归数据：

• sklearn.datasets.make_regression

class make_regression(n_samples=100, n_features=100, n_informative=10, n_targets=1, bias=0.0, effective_rank=None, tail_strength=0.5, noise=0.0, shuffle=True, coef=False, random_state=None)
  """
  生成用于回归的数据集

  :param n_samples:int，optional（default = 100)，样本数量

  :param  n_features:int,optional（default = 100)，特征数量

  :param  coef:boolean，optional（default = False），如果为True，则返回底层线性模型的系数

  :param random_state:int，RandomState实例或无，可选（默认=无）
    如果int，random_state是随机数生成器使用的种子; 如果RandomState的实例，random_state是随机数生成器; 如果没有，随机数生成器所使用的RandomState实例np.random

  :return :X,特征数据集；y,目标值
  """

from sklearn.datasets.samples_generator import make_regression
X, y = make_regression(n_samples=200, n_features=5000, random_state=42)

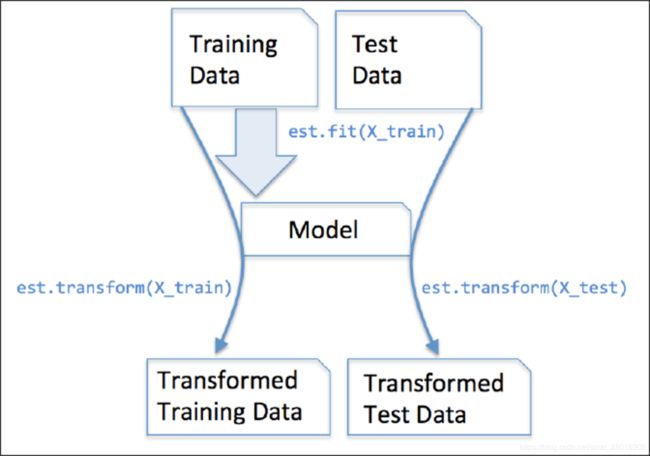
estimator的工作流程

在sklearn中，估计器(estimator)是一个重要的角色，分类器和回归器都属于estimator。在估计器中有有两个重要的方法是fit和transform。

• fit方法用于从训练集中学习模型参数
• transform用学习到的参数转换数据
  

K-近邻算法(KNN)

KNN算法最早是1968年由 Cover 和 Hart出的一种分类算法，应用场景有字符识别、文本分类、图像识别等领域提。如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。
实现流程

• 计算已知类别数据集中的点与当前点之间的距离
• 按距离递增次序排序
• 选取与当前点距离最小的k个点
• 统计前k个点所在的类别出现的频率
• 返回前k个点出现频率最高的类别作为当前点的预测分类

距离公式
两个样本的距离可以通过如下公式计算，又叫欧式距离


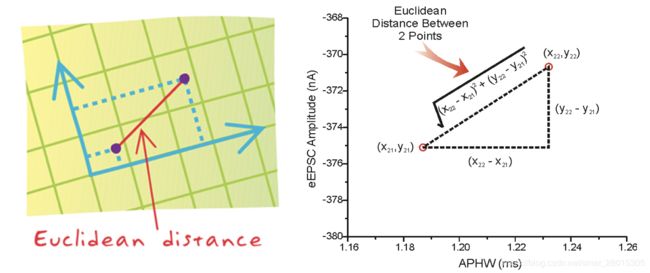
电影类型分析

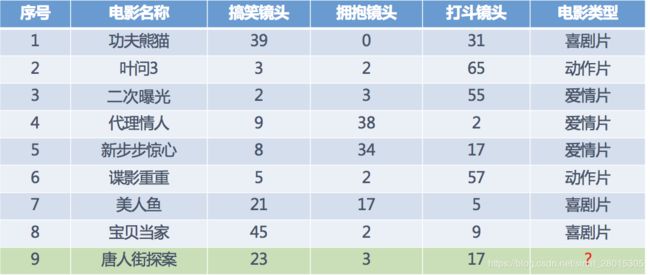
其中？ 号电影不知道类别，可以利用K近邻算法的思想去预测？类别

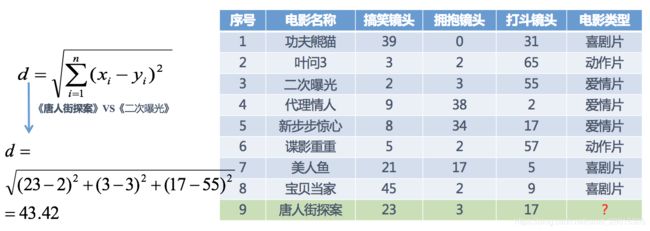
分别计算每个电影和被预测电影的距离，然后求解

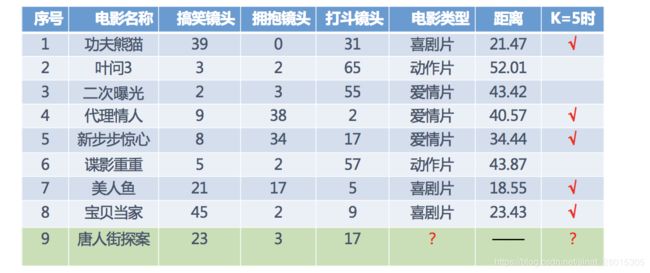
机器学习流程

• 获取数据集
• 数据基本处理
• 特征工程
• 机器学习
• 模型评估

K-近邻算法API

• sklearn.neighbors.KNeighborsClassifier(n_neighbors=5)
  • n_neighbors：int,可选（默认= 5），k_neighbors查询默认使用的邻居数

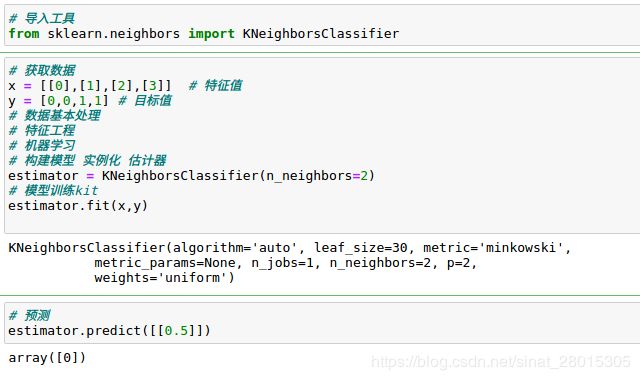
from sklearn.neighbors import KNeighborsClassifier
# 构造数据集
x = [[0], [1], [2], [3]]  # 特征值
y = [0, 0, 1, 1] # 目标值

estimator = KNeighborsClassifier(n_neighbors = 2)
# 训练数据集
estimator.fit(x,y)

# 预测
estimator.predict([[0.5]])

距离度量

• 欧式距离(Euclidean Distance)：
  欧氏距离是最容易直观理解的距离度量方法
  

• 曼哈顿距离(Manhattan Distance)：
  在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。
  
  

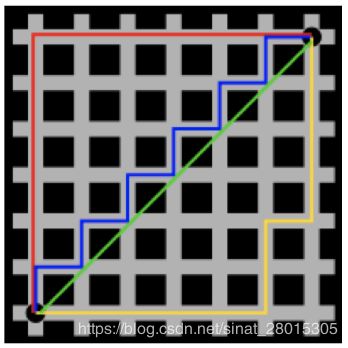
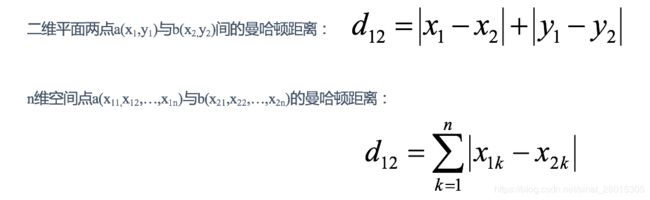
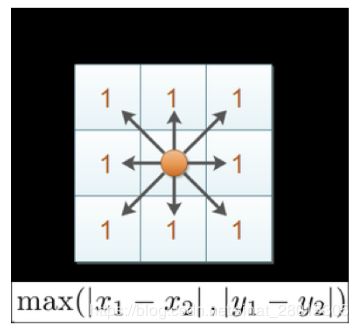
• 切比雪夫距离 (Chebyshev Distance)：
  国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。
  
  

• 闵可夫斯基距离(Minkowski Distance)：
  闵氏距离不是一种距离，而是一组距离的定义，是对多个距离度量公式的概括性的表述。
  两个n维变量a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：
  
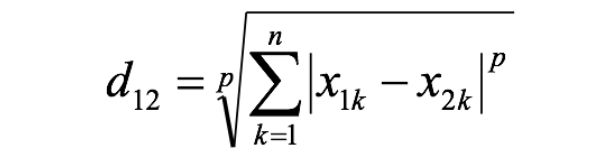
  其中p是一个变参数：
  当p=1时，就是曼哈顿距离；
  当p=2时，就是欧氏距离；
  当p→∞时，就是切比雪夫距离;
  根据p的不同，闵氏距离可以表示某一类/种的距离。

  闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点:
  e.g. 二维样本(身高[单位:cm],体重[单位:kg]),现有三个样本：a(180,50)，b(190,50)，c(180,60)。
  a与b的闵氏距离（无论是曼哈顿距离、欧氏距离或切比雪夫距离）等于a与c的闵氏距离。但实际上身高的10cm并不能和体重的10kg划等号。

  闵氏距离的缺点：
  将各个分量的量纲(scale)，也就是“单位”相同的看待了;
  未考虑各个分量的分布（期望，方差等）可能是不同的。

• 标准化欧氏距离 (Standardized EuclideanDistance)：
  既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。假设样本集X的均值(mean)为m，标准差(standard deviation)为s，X的“标准化变量”表示为：
  
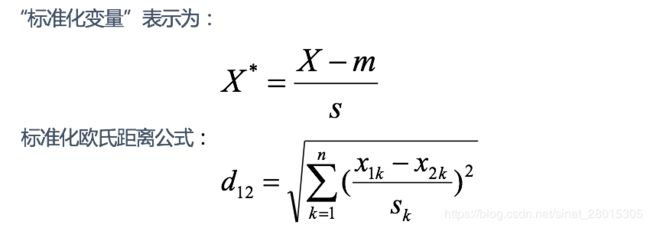
  标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。

• 余弦距离(Cosine Distance)
  几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。
  二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：
  
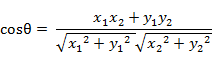
  两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为：
  
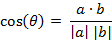
  即：
  
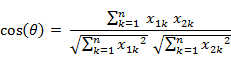
  夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。

• 汉明距离(Hamming Distance)
  两个等长字符串s1与s2的汉明距离为：将其中一个变为另外一个所需要作的最小字符替换次数。
  
  汉明重量：是字符串相对于同样长度的零字符串的汉明距离，也就是说，它是字符串中非零的元素个数：对于二进制字符串来说，就是 1 的个数，所以 11101 的汉明重量是 4。因此，如果向量空间中的元素a和b之间的汉明距离等于它们汉明重量的差a-b。
  应用：汉明重量分析在包括信息论、编码理论、密码学等领域都有应用。比如在信息编码过程中，为了增强容错性，应使得编码间的最小汉明距离尽可能大。但是，如果要比较两个不同长度的字符串，不仅要进行替换，而且要进行插入与删除的运算，在这种场合下，通常使用更加复杂的编辑距离等算法。

• 杰卡德距离(Jaccard Distance)
  杰卡德相似系数(Jaccard similarity coefficient)：两个集合A和B的交集元素在A，B的并集中所占的比例，称为两个集合的杰卡德相似系数，用符号J(A,B)表示：
  
  杰卡德距离(Jaccard Distance)：与杰卡德相似系数相反，用两个集合中不同元素占所有元素的比例来衡量两个集合的区分度：
  

k值的选择

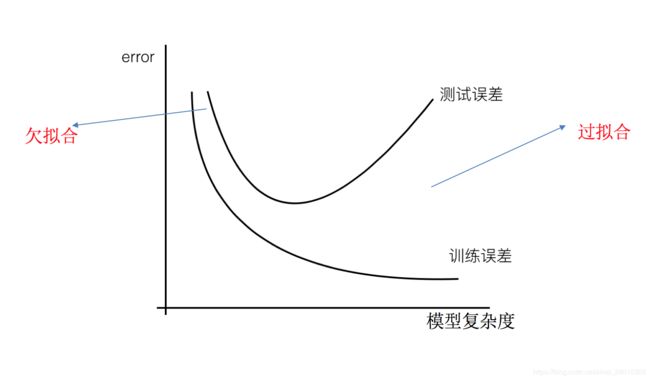
K值过小：
​容易受到异常点的影响
模型变得复杂，容易过拟合

k值过大：
​受到样本均衡的问题
模型变的简单，容易欠拟合

在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是把训练数据在分成两组:训练集和验证集）来选择最优的K值。对这个简单的分类器进行泛化，用核方法把这个线性模型扩展到非线性的情况，具体方法是把低维数据集映射到高维特征空间。

近似误差和估计误差

近似误差：对现有训练集的训练误差，关注训练集，如果近似误差过小可能会出现过拟合的现象，对现有的训练集能有很好的预测，但是对未知的测试样本将会出现较大偏差的预测。模型本身不是最接近最佳模型。

估计误差：可以理解为对测试集的测试误差，关注测试集，估计误差小说明对未知数据的预测能力好，模型本身最接近最佳模型。

kd树

实现k近邻法时，主要考虑的问题是如何对训练数据进行快速k近邻搜索。
这在特征空间的维数大及训练数据容量大时尤其必要。
k近邻法最简单的实现是线性扫描（穷举搜索），即要计算输入实例与每一个训练实例的距离。计算并存储好以后，再查找K近邻。当训练集很大时，计算非常耗时。
为了提高kNN搜索的效率，可以考虑使用特殊的结构存储训练数据，以减小计算距离的次数。

根据KNN每次需要预测一个点时，都需要计算训练数据集里每个点到这个点的距离，然后选出距离最近的k个点进行投票。当数据集很大时，这个计算成本非常高，针对N个样本，D个特征的数据集，其算法复杂度为O（DN^2）。
kd树：为了避免每次都重新计算一遍距离，算法会把距离信息保存在一棵树里，这样在计算之前从树里查询距离信息，尽量避免重新计算。其基本原理是，如果A和B距离很远，B和C距离很近，那么A和C的距离也很远。有了这个信息，就可以在合适的时候跳过距离远的点。
这样优化后的算法复杂度可降低到O（DNlog（N））

原理

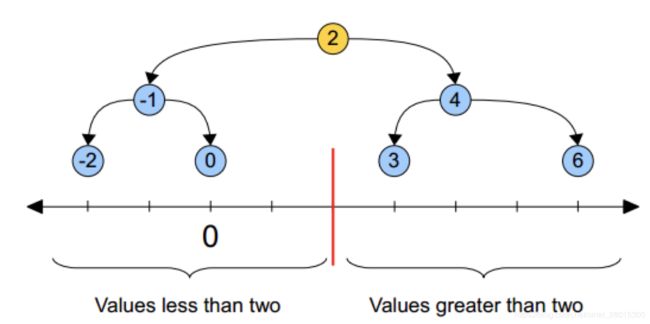
黄色的点作为根节点，上面的点归左子树，下面的点归右子树，接下来再不断地划分，分割的那条线叫做分割超平面（splitting hyperplane），在一维中是一个点，二维中是线，三维的是面。

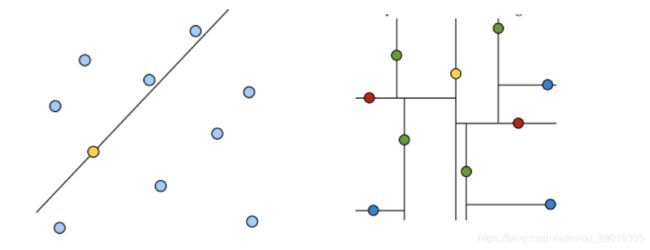
黄色节点就是Root节点，下一层是红色，再下一层是绿色，再下一层是蓝色。

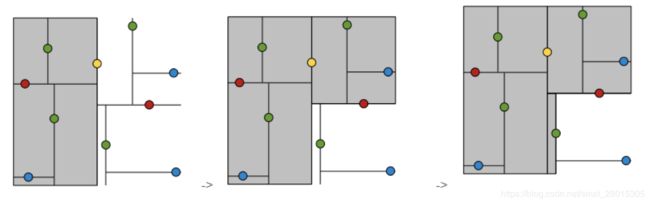
1.树的建立；
2.最近邻域搜索（Nearest-Neighbor Lookup）
kd树(K-dimension tree)是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是一种二叉树，表示对k维空间的一个划分，构造kd树相当于不断地用垂直于坐标轴的超平面将K维空间切分，构成一系列的K维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。利用kd树可以省去对大部分数据点的搜索，从而减少搜索的计算量。

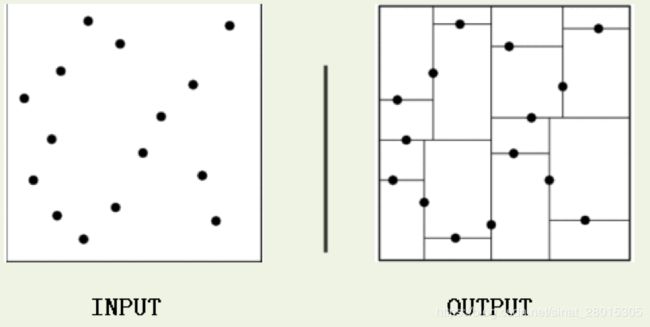
类比“二分查找”：给出一组数据：[9 1 4 7 2 5 0 3 8]，要查找8。如果挨个查找（线性扫描），那么将会把数据集都遍历一遍。而如果排一下序那数据集就变成了：[0 1 2 3 4 5 6 7 8 9]，按前一种方式我们进行了很多没有必要的查找，现在如果我们以5为分界点，那么数据集就被划分为了左右两个“簇” [0 1 2 3 4]和[6 7 8 9]。
因此，根本就没有必要进入第一个簇，可以直接进入第二个簇进行查找。把二分查找中的数据点换成k维数据点，这样的划分就变成了用超平面对k维空间的划分。空间划分就是对数据点进行分类，“挨得近”的数据点就在一个空间里面。

构造方法

（1）构造根结点，使根结点对应于K维空间中包含所有实例点的超矩形区域；
（2）通过递归的方法，不断地对k维空间进行切分，生成子结点。在超矩形区域上选择一个坐标轴和在此坐标轴上的一个切分点，确定一个超平面，这个超平面通过选定的切分点并垂直于选定的坐标轴，将当前超矩形区域切分为左右两个子区域（子结点）；这时，实例被分到两个子区域。
（3）上述过程直到子区域内没有实例时终止（终止时的结点为叶结点）。在此过程中，将实例保存在相应的结点上。
（4）通常，循环的选择坐标轴对空间切分，选择训练实例点在坐标轴上的中位数为切分点，这样得到的kd树是平衡的（平衡二叉树：它是一棵空树，或其左子树和右子树的深度之差的绝对值不超过1，且它的左子树和右子树都是平衡二叉树）。
KD树中每个节点是一个向量，和二叉树按照数的大小划分不同的是，KD树每层需要选定向量中的某一维，然后根据这一维按左小右大的方式划分数据。在构建KD树时，关键需要解决2个问题：
（1）选择向量的哪一维进行划分；
（2）如何划分数据；
第一个问题简单的解决方法可以是随机选择某一维或按顺序选择，但是更好的方法应该是在数据比较分散的那一维进行划分（分散的程度可以根据方差来衡量）。好的划分方法可以使构建的树比较平衡，可以每次选择中位数来进行划分，这样问题2也得到了解决。

案例分析

树的建立

给定一个二维空间数据集：T={(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，构造一个平衡kd树。

根结点对应包含数据集T的矩形，选择x(1)轴，6个数据点的x(1)坐标中位数是6，这里选最接近的(7,2)点，以平面x(1)=7将空间分为左、右两个子矩形（子结点）；接着左矩形以x(2)=4分为两个子矩形（左矩形中{(2,3),(5,4),(4,7)}点的x(2)坐标中位数正好为4），右矩形以x(2)=6分为两个子矩形，如此递归，最后得到如下图所示的特征空间划分和kd树。

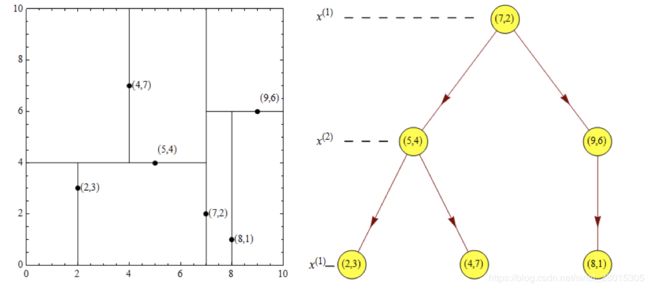
最近领域的搜索

假设标记为星星的点是 test point， 绿色的点是找到的近似点，在回溯过程中，需要用到一个队列，存储需要回溯的点，在判断其他子节点空间中是否有可能有距离查询点更近的数据点时，做法是以查询点为圆心，以当前的最近距离为半径画圆，这个圆称为候选超球（candidate hypersphere），如果圆与回溯点的轴相交，则需要将轴另一边的节点都放到回溯队列里面来。

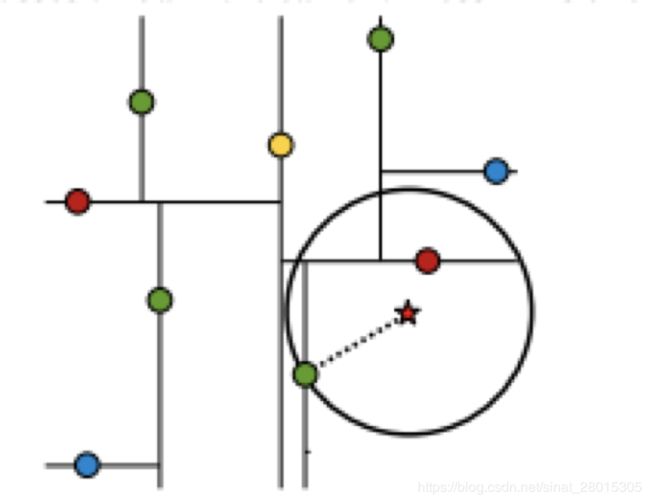
样本集{(2,3),(5,4), (9,6), (4,7), (8,1), (7,2)}

查找点(2.1,3.1)

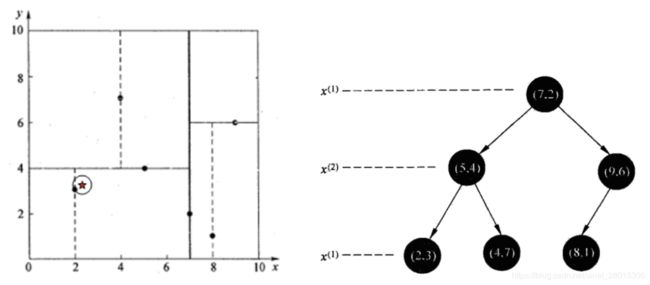
在(7,2)点测试到达(5,4)，在(5,4)点测试到达(2,3)，然后search_path中的结点为<(7,2),(5,4), (2,3)>，从search_path中取出(2,3)作为当前最佳结点nearest, dist为0.141；
然后回溯至(5,4)，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆，并不和超平面y=4相交，如上图，所以不必跳到结点(5,4)的右子空间去搜索，因为右子空间中不可能有更近样本点了。
于是再回溯至(7,2)，同理，以(2.1,3.1)为圆心，以dist=0.141为半径画一个圆并不和超平面x=7相交，所以也不用跳到结点(7,2)的右子空间去搜索。
至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2.1,3.1)的最近邻点，最近距离为0.141。

查找点(2,4.5)

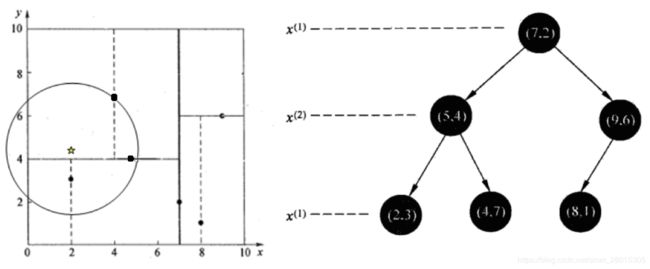
在(7,2)处测试到达(5,4)，在(5,4)处测试到达(4,7)【优先选择在本域搜索】，然后search_path中的结点为<(7,2),(5,4), (4,7)>，从search_path中取出(4,7)作为当前最佳结点nearest, dist为3.202；
然后回溯至(5,4)，以(2,4.5)为圆心，以dist=3.202为半径画一个圆与超平面y=4相交，所以需要跳到(5,4)的左子空间去搜索。所以要将(2,3)加入到search_path中，现在search_path中的结点为<(7,2),(2, 3)>；另外，(5,4)与(2,4.5)的距离为3.04 < dist = 3.202，所以将(5,4)赋给nearest，并且dist=3.04。
回溯至(2,3)，(2,3)是叶子节点，直接平判断(2,3)是否离(2,4.5)更近，计算得到距离为1.5，所以nearest更新为(2,3)，dist更新为(1.5)
回溯至(7,2)，同理，以(2,4.5)为圆心，以dist=1.5为半径画一个圆并不和超平面x=7相交, 所以不用跳到结点(7,2)的右子空间去搜索。
至此，search_path为空，结束整个搜索，返回nearest(2,3)作为(2,4.5)的最近邻点，最近距离为1.5。

总结

首先通过二叉树搜索（比较待查询节点和分裂节点的分裂维的值，小于等于就进入左子树分支，大于就进入右子树分支直到叶子结点），顺着“搜索路径”很快能找到最近邻的近似点，也就是与待查询点处于同一个子空间的叶子结点；
然后再回溯搜索路径，并判断搜索路径上的结点的其他子结点空间中是否可能有距离查询点更近的数据点，如果有可能，则需要跳到其他子结点空间中去搜索（将其他子结点加入到搜索路径）。
重复这个过程直到搜索路径为空。

案例：鸢尾花种类预测

Iris数据集是常用的分类实验数据集，由Fisher, 1936收集整理。Iris也称鸢尾花卉数据集，是一类多重变量分析的数据集。关于数据集的具体介绍：

sklearn数据集返回值介绍

• load和fetch返回的数据类型datasets.base.Bunch(字典格式)
• data：特征数据数组，是 [n_samples * n_features] 的二维 numpy.ndarray 数组
• target：标签数组，是 n_samples 的一维 numpy.ndarray 数组
• DESCR：数据描述
• feature_names：特征名,新闻数据，手写数字、回归数据集没有
• target_names：标签名

from sklearn.datasets import load_iris
# 获取鸢尾花数据集
iris = load_iris()
print("鸢尾花数据集的返回值：\n", iris)
# 返回值是一个继承自字典的Bench
print("鸢尾花的特征值:\n", iris["data"])
print("鸢尾花的目标值：\n", iris.target)
print("鸢尾花特征的名字：\n", iris.feature_names)
print("鸢尾花目标值的名字：\n", iris.target_names)
print("鸢尾花的描述：\n", iris.DESCR)

查看数据分布

seaborn.lmplot() 是一个非常有用的方法，它会在绘制二维散点图时，自动完成回归拟合

• sns.lmplot() 里的 x, y 分别代表横纵坐标的列名,
• data= 是关联到数据集,
• hue=*代表按照 species即花的类别分类显示,
• fit_reg=是否进行线性拟合。

%matplotlib inline  
# 内嵌绘图
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd

# 把数据转换成dataframe的格式
iris_d = pd.DataFrame(iris['data'], columns = ['Sepal_Length', 'Sepal_Width', 'Petal_Length', 'Petal_Width'])
iris_d['Species'] = iris.target

def plot_iris(iris, col1, col2):
    sns.lmplot(x = col1, y = col2, data = iris, hue = "Species", fit_reg = False)
    plt.xlabel(col1)
    plt.ylabel(col2)
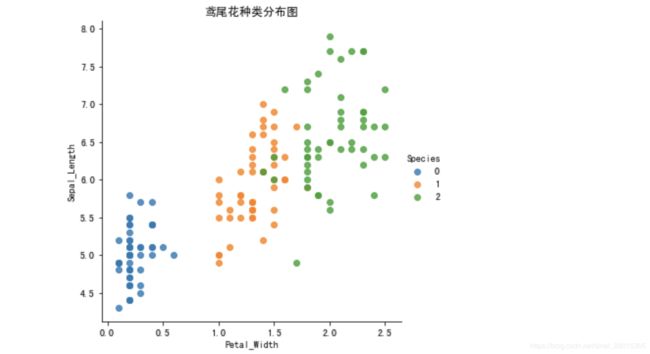
    plt.title('鸢尾花种类分布图')
    plt.show()
plot_iris(iris_d, 'Petal_Width', 'Sepal_Length')

数据集的划分

机器学习一般的数据集会划分为两个部分：

• 训练数据：用于训练，构建模型
• 测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

• 训练集：70% 80% 75%
• 测试集：30% 20% 25%

sklearn.model_selection.train_test_split(arrays, *options)

• x 数据集的特征值
• y 数据集的标签值
• test_size 测试集的大小，一般为float
• random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
• return 测试集特征训练集特征值值，训练标签，测试标签(默认随机取)

from sklearn.model_selection import train_test_split
# train_test_split(特征值,目标值,测试集划比例分为20%,随机种子=10) 随机种子相同,划分结果相同
# 返回值为训练集的特征值,测试集的特征值,训练集的目标值,测试集的目标值
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size = 0.2,random_state=10)

特征预处理

sklearn.preprocessing

特征的单位或者大小相差较大，或者某特征的方差相比其他的特征要大出几个数量级，容易影响（支配）目标结果，使得一些算法无法学习到其它的特征
需要用到一些方法进行去量纲化，使不同规格的数据转换到同一规格

• 归一化
• 标准化

归一化

通过对原始数据进行变换把数据映射到(默认为[0,1])之间

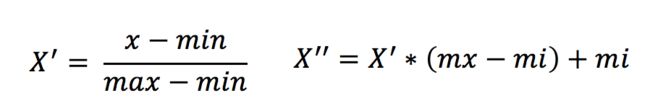
sklearn.preprocessing.MinMaxScaler (feature_range=(0,1)… )

• MinMaxScalar.fit_transform(X)
  • X:numpy array格式的数据[n_samples,n_features]
• 返回值：转换后的形状相同的array

import pandas as pd
from sklearn.preprocessing import MinMaxScaler

def minmax_demo():
    """
    归一化演示
    :return: None
    """
    data = pd.read_csv("dating.txt")
    print(data)
    # 1、实例化一个转换器类
    transfer = MinMaxScaler(feature_range=(2, 3))
    # 2、调用fit_transform
    data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
    print("最小值最大值归一化处理的结果：\n", data)

    return None

import pandas as pd 
from sklearn.preprocessing import MinMaxScaler

# 读取数据
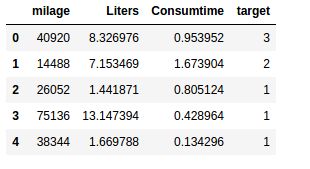
data = pd.read_csv('/home/python/Desktop/test_data/dating.txt')
data.head()

# 归一化处理  转换器 
# 实例化转换器
transform = MinMaxScaler()
# fit计算转换数据的参数即max和min,将结果保存再转换器中
transform.fit(data.iloc[:,:3]) # 用前3列数据
# 转换数据 
transform.transform(data.iloc[:,:3]) 

# 若计算和转换一步执行
transform.fit_transform(data.iloc[:,:3])  

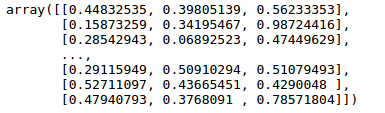
归一化方法容易受到异常值影响，鲁棒性交叉，只适合传统精确小数据场景。

标准化

通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内

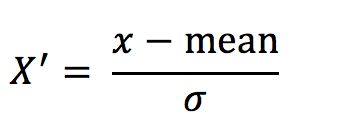
• 对于归一化来说：如果出现异常点，影响了最大值和最小值，那么结果显然会发生改变
• 对于标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小。

sklearn.preprocessing.StandardScaler( )

• 处理之后每列来说所有数据都聚集在均值0附近标准差差为1
• StandardScaler.fit_transform(X)
  • X:numpy array格式的数据[n_samples,n_features]
• 返回值：转换后的形状相同的array

import pandas as pd
from sklearn.preprocessing import StandardScaler

def stand_demo():
    """
    标准化演示
    :return: None
    """
    data = pd.read_csv("dating.txt")
    print(data)
    # 1、实例化一个转换器类
    transfer = StandardScaler()
    # 2、调用fit_transform
    data = transfer.fit_transform(data[['milage','Liters','Consumtime']])
    print("标准化的结果:\n", data)
    print("每一列特征的平均值：\n", transfer.mean_)
    print("每一列特征的方差：\n", transfer.var_)

    return None

from sklearn.preprocessing import StandardScaler
transform = StandardScaler()
# 转换数据
transform.fit_transform(data.iloc[:,:3])

在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

案例：鸢尾花种类预测—流程实现

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=‘auto’)

• n_neighbors：
  int,可选（默认= 5），k_neighbors查询默认使用的邻居数
• algorithm：{‘auto’，‘ball_tree’，‘kd_tree’，‘brute’}
  • 快速k近邻搜索算法，默认参数为auto，可以理解为算法自己决定合适的搜索算法。除此之外，用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索，
  • brute是蛮力搜索，也就是线性扫描，当训练集很大时，计算非常耗时。
  • kd_tree，构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。
  • ball tree是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

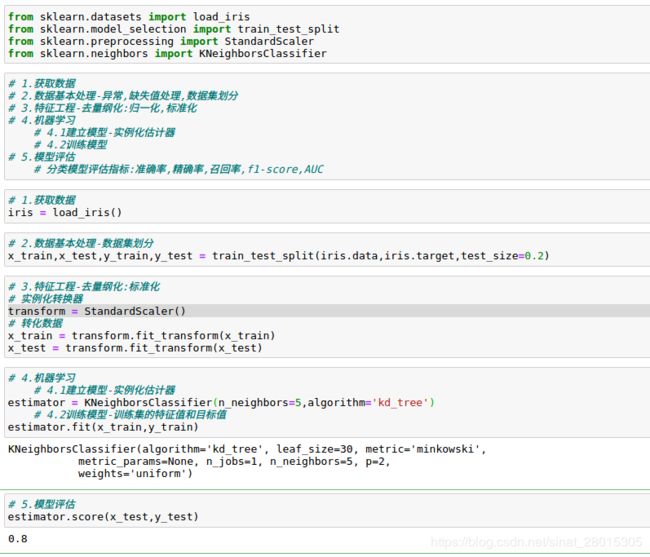
# 1.获取数据集
iris = load_iris()

# 2.数据基本处理
# x_train,x_test,y_train,y_test为训练集特征值、测试集特征值、训练集目标值、测试集目标值
x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, test_size=0.2, random_state=22)

# 3、特征工程：标准化
transform = StandardScaler()
x_train = transform.fit_transform(x_train)
x_test = transform.transform(x_test)

# 4、机器学习(模型训练)
estimator = KNeighborsClassifier(n_neighbors=9)
estimator.fit(x_train, y_train)

# 5、模型评估
# 方法1：比对真实值和预测值
y_predict = estimator.predict(x_test)
print("预测结果为:\n", y_predict)
print("比对真实值和预测值：\n", y_predict == y_test)
# 方法2：直接计算准确率
score = estimator.score(x_test, y_test)
print("准确率为：\n", score)

k近邻算法

• 优点：
  • 简单有效
  • 重新训练的代价低
  • 适合类域交叉样本
    • KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。
  • 适合大样本自动分类
    • 该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。
• 缺点：
  • 惰性学习
    • KNN算法是懒散学习方法（lazy learning,基本上不学习），一些积极学习的算法要快很多
  • 类别评分不是规格化
    • 不像一些通过概率评分的分类
  • 输出可解释性不强
    • 例如决策树的输出可解释性就较强
  • 对不均衡的样本不擅长
    • 当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入 一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。可以采用权值的方法（和该样本距离小的邻居权值大）来改进。
  • 计算量较大
    • 目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

交叉验证，网格搜索

交叉验证

将拿到的训练数据，分为训练和验证集。以下图为例：将数据分成4份，其中一份作为验证集。然后经过4次(组)的测试，每次都更换不同的验证集。即得到4组模型的结果，取平均值作为最终结果。又称4折交叉验证。
数据分为训练集和测试集，但是为了让从训练得到模型结果更加准确。做以下处理
训练集：训练集+验证集
测试集：测试集
交叉验证目的：为了让被评估的模型更加准确可信

网格搜索(Grid Search)

很多参数是需要手动指定的（如k-近邻算法中的K值），这种叫超参数。但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

交叉验证，网格搜索（模型选择与调优）API：

sklearn.model_selection.GridSearchCV(estimator, param_grid=None,cv=None)
对估计器的指定参数值进行详尽搜索

• estimator：估计器对象
• param_grid：估计器参数(dict){“n_neighbors”:[1,3,5]}
• cv：指定几折交叉验证
• fit：输入训练数据
• score：准确率
• 结果分析：
  • bestscore__:在交叉验证中验证的最好结果
  • bestestimator：最好的参数模型
  • cvresults:每次交叉验证后的验证集准确率结果和训练集准确率结果

鸢尾花案例增加K值调优

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV

# 1.获取数据
iris = load_iris()
# 2.数据基本处理-数据集划分
x_train,x_test,y_train,y_test = train_test_split(iris.data,iris.target,test_size=0.2)
# 3.特征工程-去量纲化:标准化
# 实例化转换器
transform = StandardScaler()
# 转化数据
x_train = transform.fit_transform(x_train)
x_test = transform.fit_transform(x_test)

# 4.机器学习
    # 4.1建立模型-实例化估计器
# estimator = KNeighborsClassifier(n_neighbors = 5,algorithm='kd_tree',)
estimator = KNeighborsClassifier(algorithm='kd_tree')
# 交叉验证和网格搜索
# a.实例化估计器
# b.构建参数字典
param_dict = {
    'n_neighbors':[1,3,5]
}
estimator_gscv = GridSearchCV(estimator,param_grid=param_dict,cv=2)
    # 4.2训练模型-训练集的特征值和目标值 
# estimator.fit(x_train,y_train)
estimator_gscv.fit(x_train,y_train)

# 5.模型评估
    # 分类模型评估指标:准确率,精确率,召回率,f1-score,AUC
# estimator.score(x_test,y_test)
estimator_gscv.score(x_test,y_test) # 得到最优模型准确率

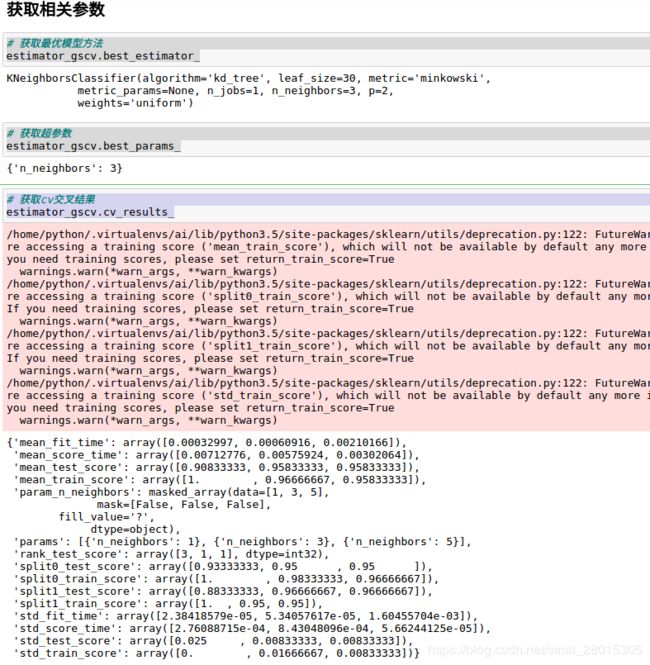
获取相关参数

# 获取最优模型方法
estimator_gscv.best_estimator_

# 获取最优超参数
estimator_gscv.best_params_

# 获取cv交叉结果
estimator_gscv.cv_results_

预测facebook签到位置

数据介绍：将根据用户的位置，准确性和时间戳预测用户正在查看的业务。

train.csv，test.csv 
row_id：登记事件的ID
xy：坐标
准确性：定位准确性 
时间：时间戳
place_id：业务的ID，这是您预测的目标

import pandas as pd 
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV

# 1.获取数据
data = pd.read_csv('/home/python/Desktop/test_data/train.csv')

# 2.数据基本处理 - 数据集划分,将时间戳提取成明显的时间特征(周几,几号,几点),剔除签到人数少的place_id
# 取部分数据进行演示
data = data.query('x>2&x<2.5& y>2&y<2.5')
# 时间转化,unit指定切出数据是以秒为单位
time = pd.to_datetime(data['time'],unit='s')
time = pd.DatetimeIndex(time)
# 增加周几,几号,几点 到数据集--特征提取
data['weekday'] = time.weekday
data['days'] = time.day
data['hour'] = time.hour
# 剔除签到人数少的place_id
# 统计place_id出现的次数--分组 
temp = data.groupby('place_id')['row_id'].count()
res = temp[temp>3].index
data = data[data['place_id'].isin(res)]
# 数据集划分
x = data[['x'],['y'],['accuracy'],['day'],['hour'],['weekday']]  # 特征值
y = data['place_id']  # 目标值
# 分割数据集
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.2)

# 3.特征工程 - 标准化
transform = StandardScaler()
x_train = transform.fit_transform(x_train)
x_test = trainsform.fit_transform(x_test)

# 4.机器学习
# 4.1创建模型
# 实例化估计器
estimator = KNeighborsClassifier(algorithm='kd_tree')
# 交叉检验和网格搜索
# 构建参数字典
param_dict={'n_neighbors':[1,3,5,7,9]}
estimator = GridSearchCV(estimator,param_grid=param_dict,cv=5)

# 4.2训练模型
estimator.fit(x_train,y_train)

# 5.模型评估 分类问题-准确率
score = estimator.score(x_test,y_test)
print('准确率为:\n',score)
# 预测值
y_predict = estimator.predict(x_test)
print('最后预测值为:\n:'y_predict)
print('预测值和真实值差距为:\n'y_predict == y_test)
# 交叉验证中的结果
print('交叉验证中最好模型为:\n',estimator.best_estimator_)
print('交叉验证中最好结果为:\n',estimator.best_score_)
print('交叉验证中最优超参数为:\n',estimator.best_params_)
print('每次交叉验证后的验证集准确率和训练集准确率为:\n',estimator.cv_results_)