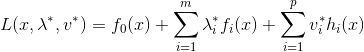沐阳听风666
沐阳听风666

凸优化第五章对偶 5.5最优性条件

5.5最优性条件

  1. 互补松弛性
  2. KKT最优性条件

互补松弛性

假设问题具有强对偶性，x^*为其原问题的最优解，(\lambda^*,v^*)为其对偶问题的最优解，可知：

f_0(x^*)=g(\lambda ^*,v^*)=\underset{x }{inf}(f_0(x)+\sum _{i=1}^m \lambda_i^* f_i(x)+\sum _{i=1}^p v^*_ih_i(x))\\

根据对偶函数的定义，可知g(\lambda ^*,v^*)小于等于任意的(f_0(x)+\sum _{i=1}^m \lambda_i^* f_i(x)+\sum _{i=1}^p v^*_ih_i(x))\\

所以取x^*时，也成立，故

f_0(x^*)=g(\lambda ^*,v^*)=\underset{x }{inf}(f_0(x)+\sum _{i=1}^m \lambda_i^* f_i(x)+\sum _{i=1}^p v^*_ih_i(x))\\ \leq (f_0(x^*)+\sum _{i=1}^m \lambda_i^* f_i(x^*)+\sum _{i=1}^p v^*_ih_i(x^*))\\

L(x,\lambda ^*,v^*)=f_0(x)+\sum _{i=1}^m \lambda_i^* f_i(x)+\sum _{i=1}^p v^*_ih_i(x)

再根据\forall x \in D,\lambda ^* \geq0,f_i(x)\leq 0,h_i(x)=0

可知

f_0(x^*)=g(\lambda ^*,v^*)=\underset{x }{inf}(f_0(x)+\sum _{i=1}^m \lambda_i^* f_i(x)+\sum _{i=1}^p v^*_ih_i(x))\\ \leq (f_0(x^*)+\sum _{i=1}^m \lambda_i^* f_i(x^*)+\sum _{i=1}^p v^*_ih_i(x^*))\\ \leq f_0(x^*)

所以上述不等式的等号成立。

推出两点：

（1）x^*最小化L(x,\lambda ^*,v^*)

（2）上式等号成立，即：

f_0(x^*)=g(\lambda ^*,v^*)=\underset{x }{inf}(f_0(x)+\sum _{i=1}^m \lambda_i^* f_i(x)+\sum _{i=1}^p v^*_ih_i(x))\\ = (f_0(x^*)+\sum _{i=1}^m \lambda_i^* f_i(x^*)+\sum _{i=1}^p v^*_ih_i(x^*))\\ = f_0(x^*)

且h_i(x^*)=0（等式约束），所以可推出

\sum _{i=1}^n\lambda_i^*f_i(x^*)=0，而\lambda _i^*\geq 0,f_i(x^*)\leq 0

所以\lambda_i^*f_i(x^*)=0,i=1,2\cdots m，成为互补松弛性。

也可写成：

\lambda^*_i> 0\Rightarrow f_i(x^*)=0\\ f_i(x^*)< 0\Rightarrow \lambda _i^*=0

KKT最优性条件

非凸问题的KKT条件

和前面一样，假设问题的约束函数和目标函数可微，x^*为其原问题的最优解，(\lambda^*,v^*)为其对偶问题的最优解，KKT条件：

f_i(x^*)\leq 0,i=1,\cdots m \\ h_i(x^*)=0,i=1,\cdots p \\ \lambda _i^*\geq 0,i=1,\cdots m\\ \lambda_i^*f_i(x^*)=0,i=1,\cdots m\\ \bigtriangledown_x L(x^*,\lambda^*,v^*)=\bigtriangledown _xf_0(x^*)+\sum_{i=1}^m\lambda^*_i\bigtriangledown _xf_i(x^*)+\sum_{i=1}^pv^*_i \bigtriangledown _xh_i(x^*)=0

称上式为Karush-Kuhn-Tucker条件，简称KKT条件。

对于目标函数和约束函数均可微的任意优化问题，如果强对偶性成立，那么任意一对原问题最优解和对偶问题最优解都必须满足KKT条件。

凸问题的KKT条件

当原问题是凸问题时，满足KKT条件的点也是原、对偶问题的最优解。

证明：假设x^*,\lambda^*,v^*满足KKT条件，且原问题是凸问题。

f_i(x^*)\leq 0,i=1,\cdots m\, \, (1) \\ h_i(x^*)=0,i=1,\cdots p \,\,(2)\\ \lambda _i^*\geq 0,i=1,\cdots m \, \,(3)\\ \lambda_i^*f_i(x^*)=0,i=1,\cdots m \,\, (4)\\ \bigtriangledown_x L(x^*,\lambda^*,v^*)=\bigtriangledown _xf_0(x^*)+\sum_{i=1}^m\lambda^*_i\bigtriangledown _xf_i(x^*)+\sum_{i=1}^pv^*_i \bigtriangledown _xh_i(x^*)=0 \, \, (5)

前两个条件表明x^*是可行解。而因为条件（3）可知

L(x,\lambda^*,v^*)=f_0(x)+\sum _{i=1}^m\lambda_i^*f_i(x)+\sum _{i=1}^pv_i^*h_i(x)是关于x的凸函数，根据条件（5）可知L在x^*处倒数为0，故x^*极小化L（根据互补松弛性也可知x^*极小化L。）

故：

g(\lambda^*,v^*)=L(x^*,\lambda^*,v^*)=f_0(x^*)+\sum _{i=1}^m \lambda_i^* f_i(x^*)+\sum _{i=1}^p v^*_ih_i(x^*) = f_0(x^*)

所以对偶间隙为0，x^*,\lambda^*,v^*分别是原问题和对偶问题的最优解。

例子

\begin{matrix} minimize \,\, -\sum_{i=1}^nlog(x_i+a_i)\\ subject \, \, to \, \, x\succeq 0,\boldsymbol{1}^Tx=1 \end{matrix}

KKT条件：

-x^*\leq 0,i=1,\cdots m\, \, (1) \\ \boldsymbol{1}^Tx^*-1=0,i=1,\cdots p \,\,(2)\\ \lambda ^*\geq 0 \, \,(3)\\ \lambda_i^*x_i^*=0 \,\, (4)\\ -\frac{1}{x_i+a_i}-\lambda_i^*+v^*=0 \, \, (5)

-x^*\leq 0,i=1,\cdots m\, \, (1) \\ \boldsymbol{1}^Tx^*-1=0,i=1,\cdots p \,\,(2)\\ \lambda ^*\geq 0 \, \,(3)\\ \lambda_i^*x_i^*=0 \,\, (4)\\ \frac{1}{x_i+a_i}+\lambda_i^*=v^* \, \, (5)

根据（5）可知v^*\geq \frac{1}{x_i+a_i}，

再看（4），考虑两种情况1）\lambda^*=0，此时x_i^*=1/v^*-a_i，v^*=1/(x_i+a_i)\leq 1/a_i。2）x^*_i=0，此时v_i^*=\lambda_i^*+1/a_i\geq 1/a_i，所以x_i^*有两种情况，

x_i^*=\left\{\begin{matrix} 0 & v\geq 1/a_i\\ 1/v-a_i & v<1/a_i \end{matrix}\right.

整理得x_i=max(0,1/v-a_i)，再根据条件（2）得到

\sum_{i=1}^nx_i=\sum_{i=1}^nmax(0,1/v-a_i)=1

 

 

 

 

 

 

 

 

 

 

你可能感兴趣的:(凸优化)

  • [插电式混合动力车辆][交替方向乘子法（ADMM）结合CVX]插电式混合动力车辆的能源管理：基于凸优化算法用于模型预测控制MPC研究（Matlab代码实现） 程序辅导帮 算法matlab人工智能
    欢迎来到本博客❤️❤️博主优势：博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。⛳️座右铭：行百里者，半于九十。本文目录如下：目录⛳️赠与读者1概述2运行结果3参考文献4Matlab代码、数据、文章⛳️赠与读者‍做科研，涉及到一个深在的思想系统，需要科研者逻辑缜密，踏实认真，但是不能只是努力，很多时候借力比努力更重要，然后还要有仰望星空的创新点和启发点。当哲学课上老师问你什么是科学，什么是电的时
  • AI大模型从0到1记录学习 大模型技术之机器学习 day27-day60 Gsen2819 算法大模型人工智能人工智能学习机器学习
    机器学习概述机器学习（MachineLearning,ML）主要研究计算机系统对于特定任务的性能，逐步进行改善的算法和统计模型。通过输入海量训练数据对模型进行训练，使模型掌握数据所蕴含的潜在规律，进而对新输入的数据进行准确的分类或预测。机器学习是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸优化、算法复杂度理论等多门学科。人工智能、机器学习与深度学习人工智能（AI）是计算机科学的一个广泛领域，
  • 凸优化：驯服复杂世界的“山谷寻宝术” 科技林总 DeepSeek学AI人工智能
    想象你被蒙上双眼，置身于一片广袤而陌生的山地。你的任务只有一个：找到最低的那个山谷。地形可能极其复杂——有无数的山峰、深谷、沟壑、平原。有些山谷是陷阱（局部最低点），而真正的宝藏（全局最低点）只有一个。如何在信息有限、地形未知的情况下，高效、可靠地找到这个绝对的最低点？这就是**凸优化（ConvexOptimization）**要解决的终极挑战。它不是普通的优化，而是一门将复杂世界转化为“友好地形
  • 詹森不等式（Jensen’s Inequality）——EM算法的基础 phoenix@Capricornus 模式识别中的数学问题机器学习
    詹森不等式（Jensen’sInequality）是数学中一个非常重要的不等式，广泛应用于概率论、统计学、凸优化、信息论等领域。它基于凸函数和凹函数的性质。一、基本定义设函数fff是定义在区间III上的凸函数（convexfunction），且随机变量XXX的取值落在III内，期望存在，则有：E[f(X)]⩾f(E[X]){E}[f(X)]\geqslantf({E}[X])E[f(X)]⩾f(E
  • 【神经网络与深度学习】通俗易懂的介绍非凸优化问题、梯度消失、梯度爆炸、模型的收敛、模型的发散 如果树上有叶子 神经网络与深度学习深度学习神经网络人工智能
    引言深度学习近年来取得了突破性的进展，并在多个领域展现出惊人的性能。然而，神经网络的训练过程并不总是顺利的，优化过程中可能会遇到各种挑战，如非凸优化问题、梯度消失、梯度爆炸、模型收敛和模型发散。这些问题直接影响着模型的稳定性和最终性能，因此理解它们对于深度学习的研究和应用至关重要。本文将深入探讨这些优化问题的本质及其应对策略，帮助你更好地掌握深度学习模型的训练过程，并提高模型的表现。深度学习中的优
  • 强化学习系统学习路径与实践方法 豆芽819 tip学习人工智能机器学习深度学习强化学习
    一、学习路径规划1.基础巩固阶段（1-2个月）必读教材：《ReinforcementLearning:AnIntroduction》(Sutton&Barto)第1-6章重点掌握：马尔可夫决策过程（MDP）、贝尔曼方程、动态规划（DP）、蒙特卡洛（MC）、时序差分（TD）算法。数学基础：概率论（期望、方差、条件概率）线性代数（矩阵运算、特征值）优化理论（梯度下降、凸优化）补充资源：MIT线性代数课
  • 最优化方法（3）:线性规划基本理论 ♚放晴♛~ 算法
    系列笔记是本人在上最优化方法时整理的，参考书籍为经典的NumericalOptimization(SecondEdition)。笔记主要分为0～5共六个部分，包括优化基础、线搜索、带约束优化基础、线性规划、对偶理论、带约束凸优化算法，以及一些零散的部分。这里是第三部分，也就是线性规划基本理论。线性规划基本理论线性规划标准形式与转化线性规划问题有着如下形式：min⁡cTxs.t.aiTx≤bi,i=
  • 《Sklearn 机器学习模型--分类模型》--支持向量机（Support Vector Machine, SVM） 非门由也 机器学习数据分析支持向量机机器学习sklearn
    支持向量机（SupportVectorMachine,SVM）是一种基于间隔最大化原理的分类模型，其核心在于构建最优超平面以区分不同类别，并具有处理高维数据的优势‌。是否高斯分布/复杂边界多项式关系输入训练数据数据标准化处理数据是否线性可分?选择线性核函数选择非线性核函数数据特征类型?使用RBF核使用多项式核构建SVM目标函数求解凸优化问题:最大化间隔得到支持向量与超平面分类新样本输出预测类别核心
  • 深度学习 常见优化器 Humingway 深度学习人工智能
    一、基础优化器随机梯度下降（SGD）•核心：∇θJ(θ)=η*∇θJ(θ)•特点：学习率固定，收敛路径震荡大•适用场景：简单凸优化问题•改进方向：动量加速二、动量系优化器2.SGDwithMomentum•公式：v_t=γv_{t-1}+η∇θJ(θ)•效果：平滑梯度更新，加速收敛•经典参数：γ=0.9（多数场景推荐）三、自适应学习率家族3.Adagrad•创新：∇θJ(θ)_t=∇θJ(θ)/(
  • 支持向量机 SVM 简要介绍 _夜空的繁星_ 机器学习svm支持向量机拉格朗日对偶机器学习
    那些我从来没有理解过的概念（1）下面是我在学习过程中遇到的对我很难理解的概念和我抄下来的笔记主要资料来源：《统计学习方法》，维基百科拉格朗日对偶问题是什么假设f(x),ci(x),hj(x)是定义在Rn上的连续可微函数，考虑以下最优化问题：$$\min_{x\inR^n}{f(x)}\c_i(x)\leq0,i=1,2,\dots,k\h_j(x)=0,j=1,2,\dots,l$$是一个凸优化问
  • 支持向量机SVM原理详解 handsomeboysk 支持向量机机器学习人工智能
    SVM原理详解1、超平面2、SVM原理1.问题定义2.分类决策得到约束条件3.最大化间隔4.优化目标3、凸优化问题1.原始优化问题优化目标约束条件2.拉格朗日乘子法3.拉格朗日函数分析4.求解对www和bbb的极值5.构造对偶问题对偶问题的约束条件：6、通过支持向量求解bbb支持向量的条件7.对偶问题的解法4、非线性如何划分1.非线性数据问题2.核技巧的核心思想3.常见的核函数1.线性核（Line
  • Python-玩转数据-凸优化 人猿宇宙 python数据挖掘人工智能
    一、说明最优化问题目前在机器学习，数据挖掘等领域应用非常广泛，因为机器学习简单来说，主要做的就是优化问题，先初始化一下权重参数，然后利用优化方法来优化这个权重，直到准确率不再是上升，迭代停止，那到底什么是最优化问题呢？比如你要从上海去北京，你可以选择搭飞机，或者火车，动车，但只给你500块钱，要求你以最快的时间到达，其中到达的时间就是优化的目标，500块钱是限制条件，选择动车，火车，或者什么火车都
  • 凸优化学习 qiaoxinyu10623 凸优化1024程序员节
    认为学习凸优化理论比较合适的路径是：学习/复习线性代数和（少量）高等数学的知识。实际上，凸优化理论综合使用了线性代数和微积分的相关知识，比如方向导数，雅克比矩阵，海森矩阵，KKT条件等。这里强烈推荐MIT公开课《线性代数》，GilbertStrang教授主讲，完全不是照本宣科，而是注重几何解释，非常具有启发性，学完之后，你会对线性代数有全新的认识。学习视频：-UP主汉语配音-【线性代数的本质】合集
  • 凸优化学习之旅 还有你Y 最优化学习
    目录标题专业名词MM算法CCP算法：代码说明SCA算法：连续松弛梯度投影算法分支定界搜索法凸问题辨别OA算法λ-representationADMM算法代码说明BCD算法BCD（BlockCoordinateDescent）代码示例与ADMM的区别总结2024年5月6日15:15:26专业名词DC问题：DifferenceofConvex。Difference理解为差，convex是凸，DC问题就
  • 运筹系列35：凸优化接口cvxpy IE06 运筹学
    1.凸优化问题1.1QP问题目标函数二阶，约束一阶，称为Quadraticprogramming1.2.QCQP目标二阶，约束二阶，QuadraticalConstraintQuadraticProgramming。1.3.SOCPsecondorderconeprogram，本质上还是一个QP问题（约束条件进行平方）。1.4DCP一个问题能够由目标函数和一系列约束构造。如果问题遵从DCP规则，这
  • 基于 Python 和 cvxpy 求解 SOCP 二阶锥规划问题 - Easy 优化python数学建模线性代数自动驾驶机器人
    cvxpy:Python功能包，为凸优化提供方便使用的用户接口，适配多种求解器SOCP:Second-OrderConeProgramming，二阶锥规划convexoptimization-凸优化，nonlinearoptimization-非线性优化timecomplexity-时间复杂度，polynomial-time-多项式时间Euclideannorm-欧几里德范数文章目录什么是SOCP
  • 机器学习 | 凸/非凸目标函数 |非凸目标函数导致求解陷入局部最优 stone_fall 图像处理与机器学习
    数学中最优化问题的一般表述是求取x∗∈χx^{*}\in\chix∗∈χ，使f(x∗)=min{f(x):x∈χ}f(x^{*})=min\{f(x):x\in\chi\}f(x∗)=min{f(x):x∈χ}，其中x是n维向量，χ\chiχ是x的可行域，f是χ\chiχ上的实值函数。凸优化问题是指χ\chiχ是闭合的凸集且f是χ\chiχ上的凸函数的最优化问题，这两个条件任一不满足则该问题即为非
  • Task10-向前分布算法和梯度提升决策树 沫2021
    1.前向分步算法前项分布算法可以解决分类问题，也可以解决回归问题。（1）Adaboost的加法模型：在Adaboost的基础上，将多个基分类器合并为一个复杂分类器，是通过计算每个基分类器的加权和。通常情况下这是一个复杂的优化问题，很难通过简单的凸优化的相关知识进行解决。而前向分步算法可以用来求解这种方式的问题，它的基本思路是：因为学习的是加法模型，如果从前向后，每一步只优化一个基函数及其系数，逐步
  • 优化｜复杂度分析——用于凸约束非凸优化问题的光滑化近似点增广拉格朗日算法 运筹OR帷幄 算法机器学习人工智能
    1.简介对于无约束的非凸优化问题，算法复杂度的下界为Ω(1/ϵ2)\Omega(1/\epsilon^2)Ω(1/ϵ2)；在目标函数光滑时，这个下界可以通过标准梯度下降算法来取到.对于带约束的非凸优化问题，这个下界依旧适用；到这里，我们自然会提出疑问：它是否也能通过某个一阶算法来取到？对此，本文[1]^{[1]}[1]作出了回答.文中介绍了一种简单的一阶算法——光滑化近似点增广拉格朗日方法（Smo
  • 03 凸优化理论-凸函数 Jay Morein 优化理论与随机控制算法
    03凸函数目录3.1凸函数的定义、性质（凸函数的判定）、示例3.2保凸运算3.4拟凸函数3.5对数凸函数3.3共轭函数3.6关于广义不等式的凸性3.1凸函数的定义、性质和例子（一）凸函数的定义&扩展值延伸3.1.1定义Def1凸函数的定义、几何含义定理1：仿射函数等价于既凸又凹函数。定理2(凸性由函数在直线上的性质刻画)*：凸函数的充要条件是与其定义域相交的任何直线上都是凸的。（可以将函数限制在直
  • 凸优化问题：基础定义 TensorME 数学理论凸优化
    “一旦将一个实际问题表述为凸优化问题，大体上意味着相应问题已经得到彻底解决，这是非凸的优化问题所不具有的性质。”——《译者序》“事实上，优化问题的分水岭不是线性与非线性，而是凸性与非凸性”——Rockafellar1什么是凸优化什么是凸优化？抛开凸优化中的种种理论和算法不谈，纯粹的看优化模型，凸优化就是：1、在最小化（最大化）的要求下，2、目标函数是一个凸函数（凹函数），3、同时约束条件所形成的可
  • 深度学习|拉格朗日对偶及KKT条件推导 科研工作站 深度学习KKT对偶仿射
    目录1主要内容2问题提出3对偶推导4KKT条件1主要内容在电力系统优化过程中，风光等分布式能源出力和负荷的不确定性（即源荷不确定性）形成了电力系统方向的研究热点，每个研究人员都试图通过自己的方法将研究推进的更深入一些，在理论研究的深层次上，离不开鲁棒优化，包括两阶段鲁棒优化、分布鲁棒优化算法等，鲁棒优化的基础知识是拉格朗日对偶和KKT条件，给大家推荐个课程——凌青老师的《凸优化》，该课程系统性讲解
  • CVX工具包（for matlab） 夕夕夕夕嘻嘻嘻嘻 编程工具matlabcvx优化
    CVX工具包（formatlab）CVX是斯坦福的教授StephenP.Bold等人开发的一个基于Matlab的凸优化工具包，能够解决诸如线性规划，二次规划，整数规划（需要license)等等优化问题，且使用非常的人性化。比如，求解最小二乘法等问题。Installation支持32／64位的Linux,MACOSX,Windows系统。可戳官方下载链接：http://cvxr.com/cvx/do
  • Matlab中CVX工具箱使用 Upsame MatlabCVXMatlab
    Matlab中CVX工具箱使用CVX是一个凸优化解决工具，需要在Matlab上使用。CVX让Matlab变成一个模型语言，可以使用Matlab的标准语法完成优化问题的求解。安装下载官方安装包，解压缩到任意路径，建议和Matlab放到一起。打开Matlab，切换路径到CVX的存放路径，Matlab中运行cvx_setup命令即完成安装。cdC:\personal\cvxcvx_setupCVX支持的
  • 【笔记】认识凸优化 假装有头像 笔记
    凸优化凸优化是一类特殊的数学优化问题，其基本思路是凸优化的基本思路是通过利用凸性质，将优化问题转化为在凸集上定义的凸函数的最优化问题，从而能够借助凸优化的理论和算法来高效求解。凸优化问题相对于一般的优化问题更易于求解以下是凸优化的基本思路和特点：凸集：凸优化中的关键概念之一是凸集。凸集是一个具有凸性质的集合，即对于集合中的任意两点，连接它们的线段仍然在集合内部。凸优化通常涉及到在凸集上定义的优化问
  • 自动驾驶轨迹规划之碰撞检测（二） 无意2121 自动驾驶轨迹规划算法游戏引擎算法自动驾驶
    欢迎大家关注我的B站：偷吃薯片的Zheng同学的个人空间-偷吃薯片的Zheng同学个人主页-哔哩哔哩视频(bilibili.com)目录1.基于凸优化2.具身足迹3.ESDF自动驾驶轨迹规划之碰撞检测（一）-CSDN博客大家可以先阅读之前的博客1.基于凸优化以此为代表的算法则是OBCA无论是自车还是障碍物都可以表示为凸多边形，因此可以表示为多个超平面围成的空间同时，自车与障碍物的避撞表达式就可以写
  • 深度学习数学知识点 搬砖成就梦想 深度学习人工智能
    一、线性代数二、概率论三、微积分四、凸优化参考资料一、线性代数书籍&视频李宏毅线性代数MITLinearAlgebra知识点1）线性空间及线性变换2）矩阵的基本概念3）状态转移矩阵4）特征向量5）矩阵的相关乘法6）矩阵的QR分解7）对称矩阵、正交矩阵、正定矩阵8）矩阵的SVD分解9）矩阵的求导10）矩阵映射/投影11）矩阵的秩12）矩阵的特征值和特征空间二、概率论书籍&视频MITIntroduct
  • 凸优化—常见分式规划解决方法及代码实现 兜兜转转m 通信仿真和学习算法
    分式规划是凸优化中常见的问题，例如最大化能效等。这篇博客介绍了single-ratio分式规划的二种常见方法。1、Quadratictransform2、Dinkelbach'sTransform优化问题一个简单的优化问题如何使用上述二种方法来计算呢？Quadratictransform代码复现%%方法2:QuadraticTransform求解max(x/(x^2+1))s.tx>=0iter_
  • 凸优化: 障碍函数法 QQ_AHAO 凸优化算法机器学习
    上一节讲到了等式消除的牛顿法，这一节我们讲一般约束问题的障碍函数法。首先我们利用对数阀函数来近似替代示性函数，用来消去不等式约束。最终使得问题变为等式约束的牛顿法，然后消除法消去等式约束，再利用牛顿法进行迭代求解。例题：求解过程：以上都是笔者个人学习方法，如有不妥之处，欢迎大家批判指正，后续有时间，笔者会分享更多的凸优化学习方法给大家。
  • 凸优化: 惩罚函数之内罚函数法（等式消除的newton法，一般约束问题的障碍函数法） QQ_AHAO 凸优化其他经验分享机器学习
    目录0.说明：1.等式约束的newton法：2.障碍函数法0.说明：相信不少小伙伴在学习内罚函数时会遇到不少障碍，接下来我将从结合个人学习过程，通过例题给小伙伴们讲解一下自己的见解，因为其理论知识在《凸优化》（王书宁译）介绍的很详细，所以我只介绍在例题中如何应用。由于外罚函数和内点法的不等式约束问题在网上都可以找到例题和求解方法，而且也相对较简单，所以在此我就多做赘述了。就讲述一下较难的等式消除的
  • springmvc 下 freemarker页面枚举的遍历输出 杨白白 enumfreemarker
    spring mvc freemarker 中遍历枚举 1枚举类型有一个本地方法叫values（），这个方法可以直接返回枚举数组。所以可以利用这个遍历。 enum public enum BooleanEnum { TRUE(Boolean.TRUE, "是"), FALSE(Boolean.FALSE, "否");
  • 实习简要总结 byalias 工作
    来白虹不知不觉中已经一个多月了，因为项目还在需求分析及项目架构阶段，自己在这段 时间都是在学习相关技术知识，现在对这段时间的工作及学习情况做一个总结： （1）工作技能方面 大体分为两个阶段，Java Web 基础阶段和Java EE阶段 1）Java Web阶段 在这个阶段，自己主要着重学习了 JSP, Servlet, JDBC, MySQL，这些知识的核心点都过 了一遍，也
  • Quartz——DateIntervalTrigger触发器 eksliang quartz
    转载请出自出处：http://eksliang.iteye.com/blog/2208559 一.概述 simpleTrigger 内部实现机制是通过计算间隔时间来计算下次的执行时间，这就导致他有不适合调度的定时任务。例如我们想每天的 1：00AM 执行任务，如果使用 SimpleTrigger，间隔时间就是一天。注意这里就会有一个问题，即当有 misfired 的任务并且恢复执行时，该执行时间
  • Unix快捷键 18289753290 unixUnix；快捷键;
    复制，删除，粘贴： dd:删除光标所在的行                             &nbs
  • 获取Android设备屏幕的相关参数 酷的飞上天空 android
    包含屏幕的分辨率  以及 屏幕宽度的最大dp 高度最大dp   TextView text = (TextView)findViewById(R.id.text); DisplayMetrics dm = new DisplayMetrics(); text.append("getResources().ge
  • 要做物联网？先保护好你的数据 蓝儿唯美 数据
    根据Beecham Research的说法，那些在行业中希望利用物联网的关键领域需要提供更好的安全性。 在Beecham的物联网安全威胁图谱上，展示了那些可能产生内外部攻击并且需要通过快速发展的物联网行业加以解决的关键领域。 Beecham Research的技术主管Jon Howes说：“之所以我们目前还没有看到与物联网相关的严重安全事件，是因为目前还没有在大型客户和企业应用中进行部署，也就
  • Java取模（求余）运算 随便小屋 java
            整数之间的取模求余运算很好求，但几乎没有遇到过对负数进行取模求余，直接看下面代码： /** * * @author Logic * */ public class Test { public static void main(String[] args) { // TODO A
  • SQL注入介绍 aijuans sql注入
    二、SQL注入范例 这里我们根据用户登录页面 <form action="" > 用户名：<input type="text" name="username"><br/> 密 码：<input type="password" name="passwor
  • 优雅代码风格 aoyouzi 代码
    总结了几点关于优雅代码风格的描述： 代码简单：不隐藏设计者的意图，抽象干净利落，控制语句直截了当。 接口清晰：类型接口表现力直白，字面表达含义，API 相互呼应以增强可测试性。 依赖项少：依赖关系越少越好，依赖少证明内聚程度高，低耦合利于自动测试，便于重构。 没有重复：重复代码意味着某些概念或想法没有在代码中良好的体现，及时重构消除重复。 战术分层：代码分层清晰，隔离明确，
  • 布尔数组 百合不是茶 java布尔数组
      androi中提到了布尔数组;   布尔数组默认的是false,  并且只会打印false或者是true   布尔数组的例子;  根据字符数组创建布尔数组 char[] c = {'p','u','b','l','i','c'}; //根据字符数组的长度创建布尔数组的个数 boolean[] b = new bool
  • web.xml之welcome-file-list、error-page bijian1013 javaweb.xmlservleterror-page
    welcome-file-list 1.定义： <welcome-file-list> <welcome-file>login.jsp</welcome> </welcome-file-list>  2.作用：用来指定WEB应用首页名称。   error-page1.定义： <error-page&g
  • richfaces 4 fileUpload组件删除上传的文件 sunjing clearRichfaces 4fileupload
     页面代码               <h:form id="fileForm">            <rich:
  • 技术文章备忘 bit1129 技术文章
    Zookeeper http://wenku.baidu.com/view/bab171ffaef8941ea76e05b8.html http://wenku.baidu.com/link?url=8thAIwFTnPh2KL2b0p1V7XSgmF9ZEFgw4V_MkIpA9j8BX2rDQMPgK5l3wcs9oBTxeekOnm5P3BK8c6K2DWynq9nfUCkRlTt9uV
  • org.hibernate.hql.ast.QuerySyntaxException: unexpected token: on near line 1解决方案 白糖_ Hibernate
    文章摘自：http://blog.csdn.net/yangwawa19870921/article/details/7553181   在编写HQL时，可能会出现这种代码： select a.name,b.age from TableA a left join TableB b on a.id=b.id  如果这是HQL，那么这段代码就是错误的，因为HQL不支持
  • sqlserver按照字段内容进行排序 bozch 按照内容排序
    在做项目的时候，遇到了这样的一个需求：           从数据库中取出的数据集，首先要将某个数据或者多个数据按照地段内容放到前面显示，例如:从学生表中取出姓李的放到数据集的前面；          select * fro
  • 编程珠玑-第一章-位图排序 bylijinnan java编程珠玑
    import java.io.BufferedWriter; import java.io.File; import java.io.FileWriter; import java.io.IOException; import java.io.Writer; import java.util.Random; public class BitMapSearch {
  • Java关于==和equals chenbowen00 java
    关于==和equals概念其实很简单，一个是比较内存地址是否相同，一个比较的是值内容是否相同。虽然理解上不难，但是有时存在一些理解误区，如下情况： 1、 String a = "aaa"; a=="aaa"; ==> true 2、 new String("aaa")==new String("aaa
  • [IT与资本]软件行业需对外界投资热情保持警惕 comsci it
          我还是那个看法,软件行业需要增强内生动力,尽量依靠自有资金和营业收入来进行经营,避免在资本市场上经受各种不同类型的风险,为企业自主研发核心技术和产品提供稳定,温和的外部环境...       如果我们在自己尚未掌握核心技术之前,企图依靠上市来筹集资金,然后使劲往某个领域砸钱,然
  • oracle 数据块结构 daizj oracle块数据块块结构行目录
    oracle 数据块是数据库存储的最小单位，一般为操作系统块的N倍。其结构为： 块头－－〉空行－－〉数据，其实际为纵行结构。 块的标准大小由初始化参数DB_BLOCK_SIZE指定。具有标准大小的块称为标准块（Standard Block）。块的大小和标准块的大小不同的块叫非标准块（Nonstandard Block）。同一数据库中，Oracle9i及以上版本支持同一数据库中同时使用标
  • github上一些觉得对自己工作有用的项目收集 dengkane github
    github上一些觉得对自己工作有用的项目收集 技能类 markdown语法中文说明 回到顶部 全文检索 elasticsearch bigdesk elasticsearch管理插件 回到顶部 nosql mapdb 支持亿级别map, list, 支持事务. 可考虑做为缓存使用 C
  • 初二上学期难记单词二 dcj3sjt126com englishword
    dangerous 危险的 panda 熊猫 lion 狮子 elephant 象 monkey 猴子 tiger 老虎 deer 鹿 snake 蛇 rabbit 兔子 duck 鸭 horse 马 forest 森林 fall 跌倒；落下 climb 爬；攀登 finish 完成；结束 cinema 电影院；电影 seafood 海鲜；海产食品 bank 银行
  • 8、mysql外键(FOREIGN KEY)的简单使用 dcj3sjt126com mysql
    一、基本概念 1、MySQL中“键”和“索引”的定义相同，所以外键和主键一样也是索引的一种。不同的是MySQL会自动为所有表的主键进行索引，但是外键字段必须由用户进行明确的索引。用于外键关系的字段必须在所有的参照表中进行明确地索引，InnoDB不能自动地创建索引。 2、外键可以是一对一的，一个表的记录只能与另一个表的一条记录连接，或者是一对多的，一个表的记录与另一个表的多条记录连接。 3、如
  • java循环标签 Foreach shuizhaosi888 标签java循环foreach
    1. 简单的for循环 public static void main(String[] args) { for (int i = 1, y = i + 10; i < 5 && y < 12; i++, y = i * 2) { System.err.println("i=" + i + " y="
  • Spring Security（05）——异常信息本地化 234390216 exceptionSpring Security异常信息本地化
    异常信息本地化          Spring Security支持将展现给终端用户看的异常信息本地化，这些信息包括认证失败、访问被拒绝等。而对于展现给开发者看的异常信息和日志信息（如配置错误）则是不能够进行本地化的，它们是以英文硬编码在Spring Security的代码中的。在Spring-Security-core-x
  • DUBBO架构服务端告警Failed to send message Response javamingtingzhao 架构DUBBO
     废话不多说，警告日志如下，不知道有哪位遇到过，此异常在服务端抛出(服务器启动第一次运行会有这个警告)，后续运行没问题，找了好久真心不知道哪里错了。    WARN 2015-07-18 22:31:15,272 com.alibaba.dubbo.remoting.transport.dispatcher.ChannelEventRunnable.run(84)
  • JS中Date对象中几个用法 leeqq JavaScriptDate最后一天
    近来工作中遇到这样的两个需求 1. 给个Date对象，找出该时间所在月的第一天和最后一天 2. 给个Date对象，找出该时间所在周的第一天和最后一天   需求1中的找月第一天很简单，我记得api中有setDate方法可以使用 使用setDate方法前，先看看getDate var date = new Date(); console.log(date); // Sat J
  • MFC中使用ado技术操作数据库 你不认识的休道人 sqlmfc
    1.在stdafx.h中导入ado动态链接库 #import"C:\Program Files\Common Files\System\ado\msado15.dll" no_namespace rename("EOF","end")2.在CTestApp文件的InitInstance()函数中domodal之前写::CoIniti
  • Android Studio加速 rensanning android studio
    Android Studio慢、吃内存！启动时后会立即通过Gradle来sync & build工程。 （1）设置Android Studio a) 禁用插件 File -> Settings...  Plugins 去掉一些没有用的插件。 比如：Git Integration、GitHub、Google Cloud Testing、Google Cloud
  • 各数据库的批量Update操作 tomcat_oracle javaoraclesqlmysqlsqlite
    MyBatis的update元素的用法与insert元素基本相同，因此本篇不打算重复了。本篇仅记录批量update操作的 sql语句，懂得SQL语句，那么MyBatis部分的操作就简单了。 　　注意：下列批量更新语句都是作为一个事务整体执行，要不全部成功，要不全部回滚。 MSSQL的SQL语句 　WITH R AS（ 　　SELECT 'John' as name, 18 as
  • html禁止清除input文本输入缓存 xp9802 input
    多数浏览器默认会缓存input的值，只有使用ctl+F5强制刷新的才可以清除缓存记录。如果不想让浏览器缓存input的值，有2种方法： 方法一： 在不想使用缓存的input中添加 autocomplete="off"; eg: <input type="text" autocomplete="off" name
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他