最优化方法 21:加速近似梯度下降方法
我们证明了梯度方法最快的收敛速度只能是 O ( 1 / k 2 ) O(1/k^2) O(1/k2)(没有强凸假设的话),但是前面的方法最多只能达到 O ( 1 / k ) O(1/k) O(1/k) 的收敛速度,那么有没有方法能达到这一极限呢?有!这一节要讲的**加速近似梯度方法(APG)**就是。这个方法的构造非常的巧妙,证明过程中会发现每一项都恰到好处的抵消了!真不知道作者是怎么想出来这么巧妙地方法,各位可以看看证明过程自行体会。
1. 加速近似梯度方法
首先说我们要考虑的优化问题形式还是
minimize f ( x ) = g ( x ) + h ( x ) \text{minimize }\quad f(x)=g(x)+h(x) minimize f(x)=g(x)+h(x)
其中 g g g 为光滑项, dom g = R n \text{dom }g=R^n dom g=Rn, h h h 为不光滑项,且为闭的凸函数,另外为了证明梯度方法的收敛性,跟前面类似,我们需要引入 Lipschitz-smooth 条件与强凸性质:
L 2 x T x − g ( x ) , g ( x ) − m 2 x T x convex \frac{L}{2}x^Tx-g(x),\quad g(x)-\frac{m}{2}x^Tx \quad \text{convex} 2LxTx−g(x),g(x)−2mxTxconvex
其中 L > 0 , m ≥ 0 L>0,m\ge0 L>0,m≥0, m m m 可以等于 0,此时就相当于没有强凸性质。
然后我们就来看看 APG(Accelerated Proximal Gradient Methods) 方法到底是怎么下降的。首先取 x 0 = v 0 , θ 0 ∈ ( 0 , 1 ] x_0=v_0,\theta_0\in(0,1] x0=v0,θ0∈(0,1],对于每次迭代过程,包括以下几个步骤:
- 求 θ k \theta_k θk: θ k 2 t k = ( 1 − θ k ) γ k + m θ k where γ k = θ k − 1 2 t k − 1 \frac{\theta_{k}^{2}}{t_{k}}=\left(1-\theta_{k}\right) \gamma_{k}+m \theta_{k} \quad \text { where } \gamma_{k}=\frac{\theta_{k-1}^{2}}{t_{k-1}} tkθk2=(1−θk)γk+mθk where γk=tk−1θk−12
- 更新 x k , v k x_k,v_k xk,vk:
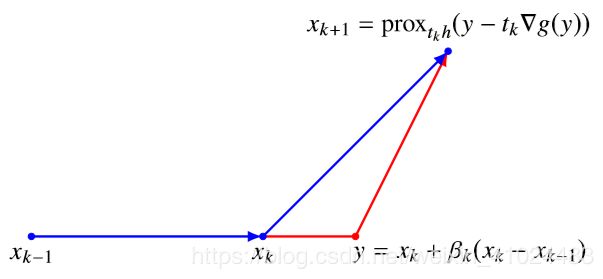
y = x k + θ k γ k γ k + m θ k ( v k − x k ) ( y = x 0 if k = 0 ) x k + 1 = prox t k h ( y − t k ∇ g ( y ) ) ( ★ ) v k + 1 = x k + 1 θ k ( x k + 1 − x k ) \begin{aligned} y &=x_{k}+\frac{\theta_{k} \gamma_{k}}{\gamma_{k}+m \theta_{k}}\left(v_{k}-x_{k}\right) \quad\left(y=x_{0} \text { if } k=0\right) \\ x_{k+1} &=\operatorname{prox}_{t_{k} h}\left(y-t_{k} \nabla g(y)\right) \quad(\bigstar)\\ v_{k+1} &=x_{k}+\frac{1}{\theta_{k}}\left(x_{k+1}-x_{k}\right) \end{aligned} yxk+1vk+1=xk+γk+mθkθkγk(vk−xk)(y=x0 if k=0)=proxtkh(y−tk∇g(y))(★)=xk+θk1(xk+1−xk)
这里面的关键就是上面的 ( ★ ) (\bigstar) (★) 式,对比前面讲过的近似梯度下降法实际上是
x k + 1 = prox t k h ( x k − t k ∇ g ( x k ) ) x_{k+1} =\operatorname{prox}_{t_{k} h}\left(x_k-t_{k} \nabla g(x_k)\right) xk+1=proxtkh(xk−tk∇g(xk))
所以这里实际上主要的变化就是将 x k x_k xk 换成了 y y y,那么 y y y 跟 x k x_k xk 又有什么不同呢?
y = x k + θ k γ k γ k + m θ k ( v k − x k ) = x k + β k ( x k − x k − 1 ) β k = θ k γ k γ k + m θ k ( 1 θ k − 1 − 1 ) = t k θ k − 1 ( 1 − θ k − 1 ) t k − 1 θ k + t k θ k − 1 2 y=x_{k}+\frac{\theta_{k} \gamma_{k}}{\gamma_{k}+m \theta_{k}}\left(v_{k}-x_{k}\right)=x_{k}+\beta_{k}\left(x_{k}-x_{k-1}\right) \\ \beta_{k}=\frac{\theta_{k} \gamma_{k}}{\gamma_{k}+m \theta_{k}}\left(\frac{1}{\theta_{k-1}}-1\right)=\frac{t_{k} \theta_{k-1}\left(1-\theta_{k-1}\right)}{t_{k-1} \theta_{k}+t_{k} \theta_{k-1}^{2}} y=xk+γk+mθkθkγk(vk−xk)=xk+βk(xk−xk−1)βk=γk+mθkθkγk(θk−11−1)=tk−1θk+tkθk−12tkθk−1(1−θk−1)
可以看到 y = x k + β k ( x k − x k − 1 ) y=x_{k}+\beta_{k}\left(x_{k}-x_{k-1}\right) y=xk+βk(xk−xk−1) 实际上就是在 x k x_k xk 的基础上增加了一个**“动量(Momentum)”**,如下图所示
我们自然的要关注 β k , θ k \beta_k,\theta_k βk,θk 的大小以及有什么性质。首先对于参数 θ k \theta_k θk 它是根据二次方程一步步迭代出来的
θ k 2 t k = ( 1 − θ k ) θ k − 1 2 t k − 1 + m θ k \frac{\theta_{k}^{2}}{t_{k}}=\left(1-\theta_{k}\right) \frac{\theta_{k-1}^{2}}{t_{k-1}}+m \theta_{k} tkθk2=(1−θk)tk−1θk−12+mθk
可以有几个主要结论:
- 如果 m > 0 m>0 m>0 且 θ 0 = m t 0 \theta_0=\sqrt{mt_0} θ0=mt0,那么有 θ k = m t k , ∀ k \theta_k=\sqrt{mt_k},\forall k θk=mtk,∀k
- 如果 m > 0 m>0 m>0 且 θ 0 ≥ m t 0 \theta_0\ge\sqrt{mt_0} θ0≥mt0,那么有 θ k ≥ m t k , ∀ k \theta_k\ge\sqrt{mt_k},\forall k θk≥mtk,∀k
- 如果 m t k < , mt_k<, mtk<,,那么有 θ k < 1 \theta_k<1 θk<1
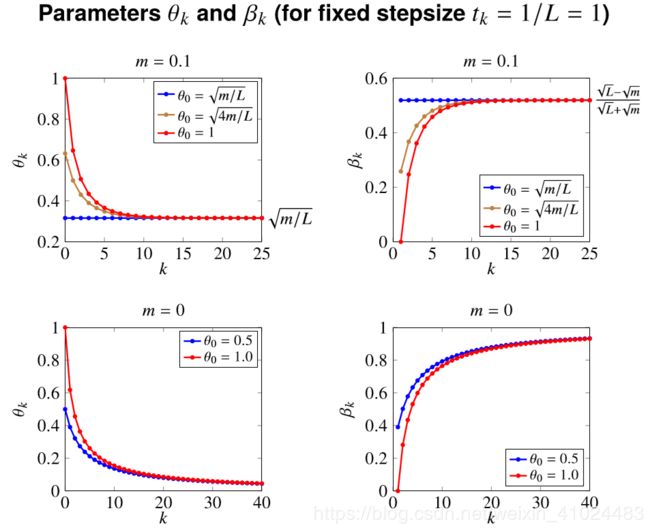
下面可以看几个关于 θ k , β k \theta_k,\beta_k θk,βk 随着迭代次数 k k k 的变化:
如果我们取前面的 APG 方法中的 m = 0 m=0 m=0,然后消掉中间变量 v k v_k vk,就可以得到 FISTA(Fast Iterative Shrinkage-Thresholding Algorithm) 算法
y = x k + θ k ( 1 θ k − 1 − 1 ) ( x k − x k − 1 ) ( y = x 0 if k = 0 ) x k + 1 = prox t k h ( y − t k ∇ g ( y ) ) \begin{aligned} y &=x_{k}+\theta_{k}\left(\frac{1}{\theta_{k-1}}-1\right)\left(x_{k}-x_{k-1}\right) \quad\left(y=x_{0} \text { if } k=0\right) \\ x_{k+1} &=\operatorname{prox}_{t_{k} h}\left(y-t_{k} \nabla g(y)\right) \end{aligned} yxk+1=xk+θk(θk−11−1)(xk−xk−1)(y=x0 if k=0)=proxtkh(y−tk∇g(y))
2. 收敛性分析
前面已经了解了基本原理,下面需要证明一下为什么他可以达到 O ( 1 / k 2 ) O(1/k^2) O(1/k2) 的收敛速度。作为类比,我们先回忆一下之前是怎么证明梯度方法/近似梯度方法的收敛性的?
( G D ) f ( x + ) − f ⋆ ≤ ∇ f ( x ) T ( x − x ⋆ ) − t 2 ∥ ∇ f ( x ) ∥ 2 2 ⟹ f ( x + ) − f ⋆ ≤ 1 2 t ( ∥ x − x ⋆ ∥ 2 2 − ∥ x + − x ⋆ ∥ 2 2 ) ( S D ) 2 t ( f ( x ) − f ⋆ ) ≤ ∥ x − x ⋆ ∥ 2 2 − ∥ x + − x ⋆ ∥ 2 2 + t 2 ∥ g ∥ 2 2 ( P D ) f ( x + ) ≤ f ( z ) + G t ( x ) T ( x − z ) − t 2 ∥ G t ( x ) ∥ 2 2 − m 2 ∥ x − z ∥ 2 2 ⟹ f ( x + ) − f ⋆ ≤ 1 2 t ( ∥ x − x ⋆ ∥ 2 2 − ∥ x + − x ⋆ ∥ 2 2 ) \begin{aligned}(GD)\quad& f\left(x^{+}\right)-f^{\star} \leq \nabla f(x)^{T}\left(x-x^{\star}\right)-\frac{t}{2}\|\nabla f(x)\|_{2}^{2}\\\Longrightarrow &f\left(x^{+}\right)-f^{\star} \leq\frac{1}{2 t}\left(\left\|x-x^{\star}\right\|_{2}^{2}-\left\|x^{+}-x^{\star}\right\|_{2}^{2}\right) \\(SD)\quad& 2 t\left(f(x)-f^{\star}\right) \leq\left\|x-x^{\star}\right\|_{2}^{2}-\left\|x^{+}-x^{\star}\right\|_{2}^{2}+t^{2}\|g\|_{2}^{2} \\(PD)\quad& f\left(x^+\right) \leq f(z)+G_{t}(x)^{T}(x-z)-\frac{t}{2}\left\|G_{t}(x)\right\|_{2}^{2}-\frac{m}{2}\|x-z\|_{2}^{2}\\\Longrightarrow &f\left(x^{+}\right)-f^{\star} \leq \frac{1}{2 t}\left(\left\|x-x^{\star}\right\|_{2}^{2}-\left\|x^{+}-x^{\star}\right\|_{2}^{2}\right)\end{aligned} (GD)⟹(SD)(PD)⟹f(x+)−f⋆≤∇f(x)T(x−x⋆)−2t∥∇f(x)∥22f(x+)−f⋆≤2t1(∥x−x⋆∥22−∥∥x+−x⋆∥∥22)2t(f(x)−f⋆)≤∥x−x⋆∥22−∥∥x+−x⋆∥∥22+t2∥g∥22f(x+)≤f(z)+Gt(x)T(x−z)−2t∥Gt(x)∥22−2m∥x−z∥22f(x+)−f⋆≤2t1(∥x−x⋆∥22−∥∥x+−x⋆∥∥22)
对于这一节的 APG 方法,证明思路是首先证明下面的迭代式子成立
f ( x i + 1 ) − f ⋆ + γ i + 1 2 ∥ v i + 1 − x ⋆ ∥ 2 2 ≤ ( 1 − θ i ) ( f ( x i ) − f ⋆ + γ i 2 ∥ v i − x ⋆ ∥ 2 2 ) if i ≥ 1 f\left(x_{i+1}\right)-f^{\star}+\frac{\gamma_{i+1}}{2}\left\|v_{i+1}-x^{\star}\right\|_{2}^{2} \\\quad \leq \left(1-\theta_{i}\right)\left(f\left(x_{i}\right)-f^{\star}+\frac{\gamma_{i}}{2}\left\|v_{i}-x^{\star}\right\|_{2}^{2}\right) \quad \text { if } i\ge1 f(xi+1)−f⋆+2γi+1∥vi+1−x⋆∥22≤(1−θi)(f(xi)−f⋆+2γi∥vi−x⋆∥22) if i≥1
对比后发现实际上之前我们考虑的是 f ( x + ) − f ⋆ f(x^+)-f^\star f(x+)−f⋆ 的迭代式子,而这里我们加了一个小尾巴,考虑 f ( x + ) − f ⋆ + γ i + 1 2 ∥ v i + 1 − x ⋆ ∥ 2 2 f(x^+)-f^\star + \frac{\gamma_{i+1}}{2}\left\|v_{i+1}-x^{\star}\right\|_{2}^{2} f(x+)−f⋆+2γi+1∥vi+1−x⋆∥22 的收敛速度。证明一会再说,有了这个迭代关系式,那么就可以有
f ( x k ) − f ⋆ ≤ λ k ( ( 1 − θ 0 ) ( f ( x 0 ) − f ⋆ ) + γ 1 − m θ 0 2 ∥ x 0 − x ⋆ ∥ 2 2 ) ≤ λ k ( ( 1 − θ 0 ) ( f ( x 0 ) − f ⋆ ) + θ 0 2 2 t 0 ∥ x 0 − x ⋆ ∥ 2 2 ) \begin{aligned}f\left(x_{k}\right)-f^{\star} & \leq \lambda_{k}\left(\left(1-\theta_{0}\right)\left(f\left(x_{0}\right)-f^{\star}\right)+\frac{\gamma_{1}-m \theta_{0}}{2}\left\|x_{0}-x^{\star}\right\|_{2}^{2}\right) \\& \leq \lambda_{k}\left(\left(1-\theta_{0}\right)\left(f\left(x_{0}\right)-f^{\star}\right)+\frac{\theta_{0}^{2}}{2 t_{0}}\left\|x_{0}-x^{\star}\right\|_{2}^{2}\right)\end{aligned} f(xk)−f⋆≤λk((1−θ0)(f(x0)−f⋆)+2γ1−mθ0∥x0−x⋆∥22)≤λk((1−θ0)(f(x0)−f⋆)+2t0θ02∥x0−x⋆∥22)
其中 λ 1 = 1 \lambda_1=1 λ1=1, λ k = ∏ i = 1 k − 1 ( 1 − θ i ) for k > 1 \lambda_{k}=\prod_{i=1}^{k-1}\left(1-\theta_{i}\right) \text { for } k>1 λk=∏i=1k−1(1−θi) for k>1,如果能证明 λ k ∼ O ( 1 / k 2 ) \lambda_k\sim O(1/k^2) λk∼O(1/k2) 就能证明收敛速度了。好了,下面就是非常巧妙而又繁琐的证明过程了。
这个证明过程很繁琐,为了更容易顺下来,这里列出来其中几个关键的等式/不等式(为了简便省略了下标):
- γ + − m θ = ( 1 − θ ) γ \gamma^+-m\theta=(1-\theta)\gamma γ+−mθ=(1−θ)γ(易证)
- γ + v + = γ + v + m θ ( y − v ) − θ G t ( y ) \gamma^+v^+=\gamma ^+ v+ m\theta(y-v)-\theta G_t(y) γ+v+=γ+v+mθ(y−v)−θGt(y)
- f ( x + ) − f ⋆ ≤ ( 1 − θ ) ( f ( x ) − f ⋆ ) − G t ( y ) T ( ( 1 − θ ) x + θ x ⋆ − y ) − t 2 ∥ G t ( y ) ∥ 2 2 − m θ 2 ∥ x ⋆ − y ∥ 2 2 \begin{aligned} f\left(x^{+}\right)-f^{\star} \leq &(1-\theta)\left(f(x)-f^{\star}\right)-G_{t}(y)^{T}\left((1-\theta) x+\theta x^{\star}-y\right) -\frac{t}{2}\left\|G_{t}(y)\right\|_{2}^{2}-\frac{m \theta}{2}\left\|x^{\star}-y\right\|_{2}^{2} \end{aligned} f(x+)−f⋆≤(1−θ)(f(x)−f⋆)−Gt(y)T((1−θ)x+θx⋆−y)−2t∥Gt(y)∥22−2mθ∥x⋆−y∥22
- γ + 2 ∥ v + − x ⋆ ∥ 2 2 ≤ γ + − m θ 2 ∥ v − x ⋆ ∥ 2 2 + G t ( y ) T ( θ x ⋆ + ( 1 − θ ) x − y ) + t 2 ∥ G t ( y ) ∥ 2 2 + m θ 2 ∥ x ⋆ − y ∥ 2 2 \begin{aligned} \frac{\gamma^{+}}{2}\left\|v^{+}-x^{\star}\right\|_{2}^{2} \leq & \frac{\gamma^{+}-m \theta}{2}\left\|v-x^{\star}\right\|_{2}^{2}+G_{t}(y)^{T}\left(\theta x^{\star}+(1-\theta) x-y\right) +\frac{t}{2}\left\|G_{t}(y)\right\|_{2}^{2}+\frac{m \theta}{2}\left\|x^{\star}-y\right\|_{2}^{2} \end{aligned} 2γ+∥∥v+−x⋆∥∥22≤2γ+−mθ∥v−x⋆∥22+Gt(y)T(θx⋆+(1−θ)x−y)+2t∥Gt(y)∥22+2mθ∥x⋆−y∥22
(3,4) 条结合就能得到上面的迭代关系式,很多项刚好消掉。下面就是要证明 λ k ∼ O ( 1 / k 2 ) \lambda_k\sim O(1/k^2) λk∼O(1/k2):
γ k + 1 = ( 1 − θ k ) γ k + m θ k λ i + 1 = ( 1 − θ i ) λ i = γ i + 1 − θ i m γ i λ i ≤ γ i + 1 γ i λ i ⟹ λ k ≤ γ k / γ 1 1 λ i + 1 − 1 λ i ≥ θ i 2 λ i + 1 = 1 2 γ 1 t i \gamma_{k+1}=(1-\theta_k)\gamma_k+m\theta_k \\\lambda_{i+1}=\left(1-\theta_{i}\right) \lambda_{i}=\frac{\gamma_{i+1}-\theta_{i} m}{\gamma_{i}} \lambda_{i} \leq \frac{\gamma_{i+1}}{\gamma_{i}} \lambda_{i} \Longrightarrow \lambda_k\le \gamma_k/\gamma_1 \\\frac{1}{\sqrt{\lambda_{i+1}}}- \frac{1}{\sqrt{\lambda_{i}}} \ge \frac{\theta_i}{2\sqrt{\lambda_{i+1}}}=\frac{1}{2}\sqrt{\gamma_1t_i} γk+1=(1−θk)γk+mθkλi+1=(1−θi)λi=γiγi+1−θimλi≤γiγi+1λi⟹λk≤γk/γ1λi+11−λi1≥2λi+1θi=21γ1ti
然后就可以有
λ k ≤ 4 ( 2 + γ 1 ∑ i = 1 k − 1 t i ) 2 = 4 t 0 ( 2 t 0 + θ 0 ∑ i = 1 k − 1 t i ) 2 \lambda_{k} \leq \frac{4}{\left(2+\sqrt{\gamma_{1}} \sum_{i=1}^{k-1} \sqrt{t_{i}}\right)^{2}}=\frac{4 t_{0}}{\left(2 \sqrt{t_{0}}+\theta_{0} \sum_{i=1}^{k-1} \sqrt{t_{i}}\right)^{2}} λk≤(2+γ1∑i=1k−1ti)24=(2t0+θ0∑i=1k−1ti)24t0
如果取 t 0 = t k = 1 / L , θ 0 = 1 t_0=t_k=1/L,\theta_0=1 t0=tk=1/L,θ0=1,则有
λ k ≤ 4 ( k + 1 ) 2 \lambda_k\le \frac{4}{(k+1)^2} λk≤(k+1)24
如果有强凸性质,也即 m > 0 m>0 m>0,那么取 θ 0 ≥ m t 0 ⟹ θ k ≥ m t k \theta_0\ge\sqrt{mt_0}\Longrightarrow \theta_k\ge \sqrt{mt_k} θ0≥mt0⟹θk≥mtk
λ k ≤ Π i = 1 k − 1 ( 1 − m t i ) \lambda_k \le \Pi_{i=1}^{k-1}(1-\sqrt{mt_i}) λk≤Πi=1k−1(1−mti)
这就可以变成线性收敛了。
最后给我的博客打个广告,欢迎光临
https://glooow1024.github.io/
https://glooow.gitee.io/
前面的一些博客链接如下
凸优化专栏
凸优化学习笔记 1:Convex Sets
凸优化学习笔记 2:超平面分离定理
凸优化学习笔记 3:广义不等式
凸优化学习笔记 4:Convex Function
凸优化学习笔记 5:保凸变换
凸优化学习笔记 6:共轭函数
凸优化学习笔记 7:拟凸函数 Quasiconvex Function
凸优化学习笔记 8:对数凸函数
凸优化学习笔记 9:广义凸函数
凸优化学习笔记 10:凸优化问题
凸优化学习笔记 11:对偶原理
凸优化学习笔记 12:KKT条件
凸优化学习笔记 13:KKT条件 & 互补性条件 & 强对偶性
凸优化学习笔记 14:SDP Representablity
最优化方法 15:梯度方法
最优化方法 16:次梯度
最优化方法 17:次梯度下降法
最优化方法 18:近似点算子 Proximal Mapping
最优化方法 19:近似梯度下降
最优化方法 20:对偶近似点梯度下降法
最优化方法 21:加速近似梯度下降方法
最优化方法 22:近似点算法 PPA
最优化方法 23:算子分裂法 & ADMM
最优化方法 24:ADMM