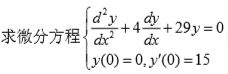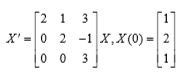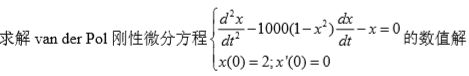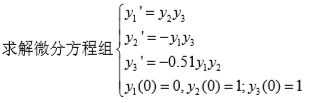matlab集训七(微分方程,级数求和)
求解微分方程(组)
1.解析解
在 MATLAB 中用 D 表示导数,例如 Dy表示 y’,D2y表示 y’’,Dy(0)=5 表示 y’(0)=5 等,符号常微分方程求解通过函数 dsolve 实现
调用格式为:
S=dsolve(eqn)
S=dsolve(eqn, cond)
S=dsolve(eqn, cond,Name,Value)
例1:![]()
syms u(t)
eqn=diff(u, t)==1+u^2;
S=dsolve(eqn);
或者:
S=dsolve('Du=1+u^2','t')
dsolve('D2y+4*Dy+29*y=0','y(0)=0,Dy(0)=15','x')
或者:
syms y(t)
eqn=diff(y, t, 2)+4*diff(y,t)+29*y==0
Dy=diff(y, t)
cond=[y(0)==0,Dy(0)==15]
S=dsolve(eqn, cond)
syms y(t) a b
eqn = diff(y,t,2) == a^2*y;
Dy = diff(y,t);
cond = [y(0)==b, Dy(0)==1];
ySol(t) = dsolve(eqn,cond)
或者
dsolve('D2y=a^2*y','y(0)=b','Dy(0)=1','t')
syms x(t) y(t) z(t)
eqns=[diff(x,t)==2*x-2*y+3, diff(y,t)==4*x-5*y+3, diff(z,t)==4*x-4*y+2];
dsolve(eqns)
syms t;
a=[2,1,3;0,2,-1;0,0,2];
x0=[1;2;1];
x=expm(a*t)*x0
pretty(x); %化简结果
syms t s;
a=[1 0 0;2 1 -2;3 2 1];
fs=[0;0;exp(s)*cos(2*s)];
x0=[0;1;1];
tx=int(expm(a*(t-s))*fs,s); %先求不定积分,再计算定积分的结果,提高速度
xstar=subs(tx,s,t)-subs(tx,s,0);
x=expm(a*t)*x0+xstar;
x=simple(s),pretty(x) %simple 直接显示化简结果,simplify显示化简过程,pretty修 改显示格式
2.数值解
ode45,ode23,ode113,ode23s,ode15s
[t,x]=solver(‘f’, ts, x0, options)
t 是自变量的值,x 是函数值,
solver 表示上述 5 种求解器的一种;
‘f’是由待解方程写成的 m 文件名,ts=[t0, tf]表示自变量的初值和 终值,options 用于设定误差限
注 1:在解 n 个未知函数的的方程组时,x0 和 xn 均为 n 维向量,m文件中的待解 方程组应以 x 分量形式写出;
注 2:使用 Matlab 求数值解时,高阶微分方程必须等价的变换成一阶微分方程组*
写成 m 文件如下所示:
function dy=fun1(t,y)
dy=zeros(2,1);
dy(1)=y(2);
dy(2)=1000*(1-y(1)^2)*y(2)-y(1);
取[t0 ,tf]=[0,3000],输入命令:
[t,y]=ode15s('fun1',[0,3000],[2,0]);
plot(t,y(:,1),'-')
解:建立方程组的 m 文件:
function dy=fun2(t,y)
dy=zeros(3,1); %必须初始化为列向量
dy(1)=y(2)*y(3);
dy(2)=y(1)*y(3);
dy(3)=-0.51*y(1)*y(2);
取 t0=0,tf=12,Matlab 命令如下:
[t,y]=ode45('fun2',[0 12],[0 1 1])
plot(t,y(:,1),'-',t,y(:,2),'*',t,y(:,3),'+')
注意:定义的微分方程组也可以含有附加参数,附加参数需要写到微分方程函数中 作为形参存在,例如 function dy=fun(t,y,a1,a2),在调用时,需要在 ode45 函数中给形参 赋予具体的数值,如[t,x]=ode45(@fun,tspan,t0,a1,a2)
解:rho=10;beta=29;lamda=8/3;
f=@(t,Y)[rho*(Y(2)-Y(1));beta*Y(1)-Y(2)-Y(1)*Y(3);-lamda*Y(3)+Y(1)*Y(2)];%方程组必须使用列向量表示
[t,y]=ode45(f,[0,30],[5,13,17])
subplot(2,2,1)
plot(t,y(:,1),'*') %x 曲线
subplot(2,2,2)
plot(t,y(:,2),'X')
subplot(2,2,3)
plot(t,y(:,3),'O')
subplot(2,2,4)
plot3(y(:,1),y(:,2),y(:,3)) %绘制空间轨迹图,可以用 comet3 绘制动画式轨迹。
3.边值问题的matlab数值解
sol = bvp4c(odefun,bcfun,solinit,options)
solinit = bvpinit(x,yinit,parameters) %该函数用来给 sol 提供初始猜测解,x 可以用 linspace(a,b,M)获得
例1:求解非线性微分方程边值问题 y’’=F(x,y,y’)=2yy’,y(0)=-1,y(pi/2)=1
%令 x1=y,x2=y',则方程化简为:x1'=x2,x2'=2x1x2
f1=@(t,x)[x(2);2*x(1)*x(2)]; %微分方程的 Matlab 函数
f2=@(xa,xb)[xa(1)+1;xb(1)-1]; %边界条件的 Matlab 函数
sinit=bvpinit(linspace(0,pi/2,5),rand(2,1));
sol=bvp5c(f1,f2,sinit);
plot(sol.x,sol.y)
**注意:如果上面的边界条件改为:y’(pi/2)=1 和 y(pi/2)-y(0)=1,
则对应的边值函数 修改为:f2=@(xa,xb)[xb(2)-1;xb(1)-xa(1)-1] **
4.时延微分方程求解函数
常数时延微分方程函数 dde23()
时变延迟的微分方程函数 ddesd()
中立型延迟微分方程函数 ddensd()

5.偏微分方程
pdepe()函数可以直接求解偏微分方程,
其入口为[c,f,s]=pdefun(x,t,u,ux);
边值函数可以由[pa,qa,pb,qb]=pdebc(x,t,u,ux)描述;
初始函数可以由 u0=pdeic(x)来描述;
sol=pdepe(m,@pdefun,@pdeic,@pdebc,x,t)
例:
function [c,f,s]=exmpde(x,t,u,du)
c=[1;1];
y=u(1)-u(2);
F=exp(-5.73*y)-exp(-11.46*y);
s=[-F;F];
f=[0.024*du(1);
0.17*du(2)];
end
function [pa,pb,qa,qb]=exmpbc(xa,ua,xb,ub,t)
pa=[0;ua(2)];
qa=[1;0];
pb=[ub(1)-1;0];
qb=[0;1];
end
u0=@(x)[1;0];
x=0:0.05:1;
t=0:0.05:2;
m=0;
sol=pdepe(m,@exmpde,u0,@exmpbc,x,t);
surf(x,t,sol(:,:,1))
figure;
surf(x,t,sol(:,:,2))
6.级数求和
r = symsum(expr, v)
r = symsum(expr, v, a, b)
例1:
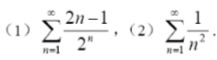
(1)
syms n
f1=(2*n-1)/2^n;
s1=symsum(f1,n,1,inf)
(2)
syms n
f2=1/n^2;
s2=symsum(f2,n,1,inf)
注::Matlab 求数组元素乘积的函数 B=prod(A) 如果 A 是一个 m 行一列的(向 量),则这种用法即返回这 m 个元素的乘积; 如果 A 是一个 m 行 n 列的矩阵,则 A 的每一列都被看做一个 m 行 1 列的向量,分别计算每个向量中元素的乘积,返回给 B,因此 B 是一个 1 行 n 列的数组
7.关于泰勒展开式的用法
taylor(fcn,x,x0,'Order',6);%对函数fcn在点x0处,进行6阶泰勒展开;