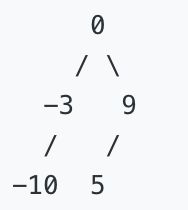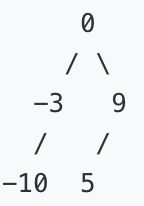力扣刷题 | 二叉树

总述

基本概念

五种基本形态：

• 空二叉树
• 只有一个根结点的二叉树
• 只有左子树
• 只有右子树
• 完全二叉树
  

类型：

• 满二叉树：除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树，即深度为$k$的满二叉树有$2^k-1$个结点
• 完全二叉树：除了最后一层外，其它层都是满的，最后一层的叶子结点都是从左到右依次排布，即深度为$k$的完全二叉树至少有$2^{k-1}$个结点，至多有$2^k-1$个结点
• 平衡二叉树（AVL）：空树或左右子树的高度差绝对值不超过1，并且左右两个子树都是平衡二叉树

相关术语：

• 树的结点：包含一个数据元素及若干指向子树的分支
• 孩子结点：结点的子树的根称为该结点的孩子
• 双亲结点：B结点是A结点的孩子，则A结点是B结点的双亲
• 兄弟结点：同一双亲的孩子结点
• 堂兄结点：同一层上结点
• 子孙结点：以某结点为根的子树中任一结点都称为该结点的子孙
• 结点层：根结点的层为1，根结点的孩子的层为2，以此类推
• 树的深度：树中最大的结点层
• 结点的度：结点子树的个数
• 树的度：树中最大的结点度
• 叶子结点（终端结点）：度为0的结点
• 分支结点：度不为0的结点
• 有序树：子树有序的树
• 无序树：不考虑子树的顺序

二叉树性质

• 在非空二叉树中，第$i$层的结点总数不超过$2^{i-1}$
• 深度为$h$的二叉树最多有$2^h-1$个结点，最少有$h$个结点
• 对于任意一棵二叉树，如果其叶节点数为$N_0$，而度数为2的结点总数为$N_2$，则有$N_0=N_2+1$
• 具有$N$个结点的完全二叉树深度为$[{\log }_{2}N]+1$，其中$[]$表示向下取整
• 具有$N$个结点的完全二叉树各结点如果用顺序方式存储，则结点之前有如下关系：
  • 编号为$i(i>1)$的结点的父结点编号为$[\frac{i}{2}]$
  • 如果$2i<=N$，则其左孩子的编号为$2i$，否则无左孩子
  • 如果$2i+1<=N$，则其右孩子的编号为$2i+1$，否则无右孩子
• 给定N个结点，能构成$h(N)$种不同的二叉树，其中$h(N)$为卡特兰数的第$N$项

二叉树遍历

遍历是对树的一种最基本的运算，所谓遍历二叉树，就是按一定的规则和顺序走遍二叉树的所有结点，使每一个结点都被访问一次，而且只被访问一次。由于二叉树是非线性结构，因此，树的遍历实质上是将二叉树的各个结点转换成为一个线性序列来表示。

设L、D、R分别表示遍历左子树、访问根结点和遍历右子树， 则对一棵二叉树的遍历有三种情况：DLR（称为先根次序遍历），LDR（称为中根次序遍历），LRD （称为后根次序遍历）。

层次遍历即按照层次访问，通常用队列来做。访问根，访问子女，再访问子女的子女（越往后的层次越低）（两个子女的级别相同）

94 二叉树的中序遍历

给定一个二叉树，返回它的中序遍历。

解法： 递归，依次对左子树、根、右子树进行输出。注意空树的情况。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        return [] if root == None else ((self.inorderTraversal(root.left) if root.left != None else []) + [root.val] + (self.inorderTraversal(root.right) if root.right != None else []))
        '''
        if root == None:
            return []
        if root.left == None:
            if root.right == None:
                return [root.val]
            else:
                return [root.val] + self.inorderTraversal(root.right)
        else:
            if root.right == None:
                return self.inorderTraversal(root.left) + [root.val]
            else:
                return self.inorderTraversal(root.left) + [root.val] + self.inorderTraversal(root.right)
        '''

95 不同的二叉搜索树2

给定一个整数 n，生成所有由 1 … n 为节点所组成的二叉搜索树。

解法： 动态规划，将1-n每个数字分别作为根节点，左子树为小于这个节点的数，右子树为大于这个节点的数

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def generateTrees(self, n: int) -> List[TreeNode]:
        def generate_trees(start, stop):
            if start > stop:
                return [None]
            elif start == stop:
                return [TreeNode(start)]
            dp = []
            for i in range(start,stop+1):
                left_trees = generate_trees(start,i-1)
                right_trees = generate_trees(i+1,stop)
                for l in left_trees:
                    for r in right_trees:
                        temp = TreeNode(i)
                        temp.left = l
                        temp.right = r
                        dp.append(temp)
            return dp
        return generate_trees(1,n) if n else []

96 不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

解法： 动态规划，依次计算1、2、……、n个节点的二叉树有多少种，i个节点的二叉树种类为对左子树包含1到i-1个节点，对应的右子树包含i-1到1个节点，求左子树种类*右子树种类的和

class Solution:
    def numTrees(self, n: int) -> int:
        dp = [1,1]
        if n >= 2:
            for i in range(2,n+1):
                temp = 0
                for j in range(i):
                    temp = temp + dp[j]*dp[i-j-1]
                dp.append(temp)
        return dp[n]

98 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：
-节点的左子树只包含小于当前节点的数。
-节点的右子树只包含大于当前节点的数。
-所有左子树和右子树自身必须也是二叉搜索树。

解法： 递归，对左/右子树分别进行遍历，其最大值/最小值分别小于/大于根节点，并对左右子树分别进行判断是否为二叉搜索树。注意对根节点、左子树、右子树存在性的判断。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def inorderTraversal(self, root: TreeNode) -> List[int]:
        return [] if root == None else ((self.inorderTraversal(root.left) if root.left != None else []) + [root.val] + (self.inorderTraversal(root.right) if root.right != None else []))
    def isValidBST(self, root: TreeNode) -> bool:
        if root == None:
            return True
        else:
            temp = self.inorderTraversal(root)
            for i in range(len(temp)-1):
                if temp[i] >= temp[i+1]:
                    return False
            return True

100 相同的树

给定两个二叉树，编写一个函数来检验它们是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

解法： 递归，对根节点、左子树、右子树分别进行判断。注意讨论根节点、左子树、右子树存在性的判断。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSameTree(self, p: TreeNode, q: TreeNode) -> bool:
        if p == None and q == None:
            return True
        elif p != None and q != None and p.val == q.val:
            if p.left == None and q.left == None:
                left = 1
            elif p.left != None and q.left != None and self.isSameTree(p.left,q.left):
                left = 1
            else:
                left = 0
            if p.right == None and q.right == None:
                right = 1
            elif p.right != None and q.right != None and self.isSameTree(p.right,q.right):
                right = 1
            else:
                right = 0
            return left*right
        else:
            return False

101 对称二叉树

给定一个二叉树，检查它是否是镜像对称的。
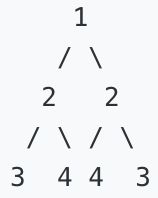
例如，二叉树 [1,2,2,3,4,4,3] 是对称的，但是下面这个 [1,2,2,null,3,null,3] 则不是镜像对称的

解法： 递归，从左右子树进行对称检查，两个子树根相等时递归检查左子树的左子树和右子树的右子树对称、左子树的右子树和右子树的左子树对称

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        def isSymmetricTwo(root_left:TreeNode,root_right:TreeNode):
            if (not root_left) and (not root_right):
                return True
            if (not root_left) or (not root_right):
                return False
            if root_left.val != root_right.val:
                return False
            return isSymmetricTwo(root_left.left, root_right.right) and isSymmetricTwo(root_left.right, root_right.left)
        if not root:
            return True
        return isSymmetricTwo(root.left, root.right)

102 二叉树的层序遍历

给你一个二叉树，请你返回其按 层序遍历 得到的节点值。 （即逐层地，从左到右访问所有节点）。
示例：二叉树：[3,9,20,null,null,15,7]，返回其层次遍历结果：

解法： 对每个节点和其深度进行递归，将该节点的值加入结果列表第深度个子列表中

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrder(self, root: TreeNode) -> List[List[int]]:
        levels = []
        def helper(root: TreeNode, level: int):
            if len(levels) == level:
                levels.append([])
            if root:
                levels[level].append(root.val)
                if root.left:
                    helper(root.left, level+1)
                if root.right:
                    helper(root.right, level+1)
        if root:
            helper(root, 0)
        return levels

103 二叉树的锯齿形层次遍历

给定一个二叉树，返回其节点值的锯齿形层次遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。
例如：给定二叉树 [3,9,20,null,null,15,7]，返回锯齿形层次遍历如下：

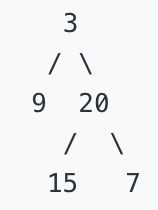
解法： 在层次遍历的基础上，检查深度的奇偶性，以确定在该深度对应的列表的第一个还是最后一个位置添加元素

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def zigzagLevelOrder(self, root: TreeNode) -> List[List[int]]:
        levels = []
        def helper(root:TreeNode, level:int):
            if len(levels) == level:
                levels.append([])
            if root:
                if level%2 == 1:
                    levels[level] = [root.val] + levels[level]
                else:
                    levels[level].append(root.val)
                if root.left:
                    helper(root.left, level+1)
                if root.right:
                    helper(root.right, level+1)
        if root:
            helper(root, 0)
        return levels

104 二叉树的最大深度

给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明：叶子节点是指没有子节点的节点。
示例：给定二叉树 [3,9,20,null,null,15,7]，返回它的最大深度 3 。

解法： ：定义递归函数，分别获取左子树和右子树的最大深度

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        level = 0
        def helper(root: TreeNode, level: int):
            if (not root.left) and (not root.right):
                return level
            left_level = helper(root.left, level + 1) if root.left else 0
            right_level = helper(root.right, level + 1) if root.right else 0
            return max(left_level, right_level)
        if not root:
            return 0
        return helper(root, 0) + 1

105 从前序与中序遍历序列构造二叉树

根据一棵树的前序遍历与中序遍历构造二叉树。
注意：你可以假设树中没有重复的元素。
例如，给出前序遍历 preorder = [3,9,20,15,7]，中序遍历 inorder = [9,3,15,20,7]，返回如下的二叉树：

解法： 分别确定左子树和右子树的前序和中序遍历，递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if len(inorder) == 0 or len(preorder) == 0:
            return None
        root = TreeNode(preorder[0])
        root_index = inorder.index(root.val)
        root_left = inorder[:root_index]
        root_right = inorder[(root_index+1):]
        root.left = TreeNode(root_left[0]) if len(root_left) == 1 else self.buildTree(preorder[1:(1+len(root_left))],root_left)
        root.right = TreeNode(root_right[0]) if len(root_right) == 1 else self.buildTree(preorder[(1+len(root_left)):],root_right)
        return root

106 从中序与后序遍历序列构造二叉树

根据一棵树的中序遍历与后续遍历构造二叉树。
注意：你可以假设树中没有重复的元素。
例如，给出中序遍历 inorder = [9,3,15,20,7]，后序遍历 postorder = [9,15,7,20,3]，返回如下的二叉树：

解法： 分别确定左子树和右子树的中序和后序遍历，递归

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
        if len(inorder) == 0 or len(postorder) == 0:
            return None
        root = TreeNode(postorder[len(postorder)-1])
        root_index = inorder.index(root.val)
        root_left = inorder[:root_index]
        root_right = inorder[(root_index+1):]
        root.left = TreeNode(root_left[0]) if len(root_left) == 1 else self.buildTree(root_left,postorder[0:len(root_left)])
        root.right = TreeNode(root_right[0]) if len(root_right) == 1 else self.buildTree(root_right,postorder[(len(root_left)):(len(postorder)-1)])
        return root

107 二叉树的层次遍历2

给定一个二叉树，返回其节点值自底向上的层次遍历。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）
例如：给定二叉树 [3,9,20,null,null,15,7]，返回其自底向上的层次遍历为：

解法： 和二叉树的层序遍历相同，仅修改为每次向列表最前端插入元素，每次向子列表添加元素时从尾部回数

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
        def helper(root: TreeNode, level: int, levels: List[List[int]]):
            if len(levels) == level:
                levels = [[]] + levels
            levels[len(levels)-1-level].append(root.val)
            if root.left:
                levels = helper(root.left, level + 1, levels)
            if root.right:
                levels = helper(root.right, level + 1, levels)
            return levels
        levels = []
        if root:
            levels = helper(root, 0, levels)
        return levels

108 将有序数组转换为二叉搜索树

将一个按照升序排列的有序数组，转换为一棵高度平衡二叉搜索树。
本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。
示例:给定有序数组: [-10,-3,0,5,9]，一个可能的答案是：[0,-3,9,-10,null,5]，它可以表示下面这个高度平衡二叉搜索树：

解法： 将有序数组拆分为根结点、左子树数组、右子树数组，递归输出左右子树
注意： 二叉搜索树要求对于所有结点，所有左子树的结点的值小于该结点的值小于所有右子树的结点的值

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sortedArrayToBST(self, nums: List[int]) -> TreeNode:
        if len(nums) == 1:
            return TreeNode(nums[0])
        if len(nums) == 0:
            return None
        root = TreeNode(nums[len(nums)//2])
        root.left = self.sortedArrayToBST(nums[:(len(nums)//2)])
        root.right = self.sortedArrayToBST(nums[(len(nums)//2 + 1):])
        return root

109 有序链表转换二叉搜索树

给定一个单链表，其中的元素按升序排序，将其转换为高度平衡的二叉搜索树。
本题中，一个高度平衡二叉树是指一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1。
示例：给定的有序链表： [-10, -3, 0, 5, 9]，一个可能的答案是：[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树：

解法： 采用多个指针，获取根结点和左右子树的链表，递归
注意： 可以采用双指针获取链表中间位置，快指针每次移动两格，慢指针每次移动一格

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sortedListToBST(self, head: ListNode) -> TreeNode:
        if not head:
            return None
        if not head.next:
            return TreeNode(head.val)
        mid_ptr = head
        front_size = 1
        size = self.getListSize(head)
        while front_size < size//2:
            front_size += 1
            mid_ptr = mid_ptr.next
        root = TreeNode(mid_ptr.next.val)
        root.right = self.sortedListToBST(mid_ptr.next.next)
        mid_ptr.next = None
        root.left = self.sortedListToBST(head)
        return root
    def getListSize(self, head: ListNode) -> int:
        size = 0
        ptr = head
        while ptr:
            size += 1
            ptr = ptr.next
        return size

中序遍历解法： 巧妙的点在于每次都先递归左子树，然后再设置根结点，最后递归右子树，通过一个指针的挪动完成树的生成，点击查看详情

# Definition for singly-linked list.
# class ListNode:
#     def __init__(self, x):
#         self.val = x
#         self.next = None

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def sortedListToBST(self, head: ListNode) -> TreeNode:
        size = 0
        p = head
        while p:
            size += 1
            p = p.next

        def rebuildTree(l, r):
            nonlocal head
            if l >= r:
                return None
            
            mid = (l+r)//2

            left = rebuildTree(l, mid)
            root = TreeNode(head.val)
            root.left = left
            
            head = head.next

            root.right = rebuildTree(mid+1, r)

            return root

        return rebuildTree(0 ,size)

110 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过1。
示例 1：给定二叉树 [3,9,20,null,null,15,7]，返回 true 。
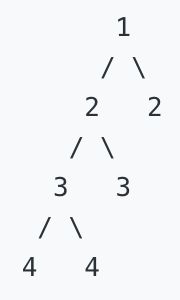
示例 2：给定二叉树 [1,2,2,3,3,null,null,4,4]，返回false。

解法： 从上到下递归，判断左右子树的高度差，满足条件再判断每个子树

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if not root:
            return True
        if abs(self.getRootHeight(root.left) - self.getRootHeight(root.right)) > 1:
            return False
        return self.isBalanced(root.left) and self.isBalanced(root.right)
    def getRootHeight(self, root: TreeNode) -> int:
        if not root:
            return 0
        return 1 + max(self.getRootHeight(root.left),self.getRootHeight(root.right))

自上至下递归解法： 避免重复计算子树高度

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def isBalanced(self, root: TreeNode) -> bool:
        if not root:
            return True
        if abs(self.getRootHeight(root.left) - self.getRootHeight(root.right)) > 1:
            return False
        return self.isBalanced(root.left) and self.isBalanced(root.right)
    def getRootHeight(self, root: TreeNode) -> int:
        if not root:
            return 0
        return 1 + max(self.getRootHeight(root.left),self.getRootHeight(root.right))

111 二叉树的最小深度

给定一个二叉树，找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。
示例：给定二叉树 [3,9,20,null,null,15,7]，返回它的最小深度 2

解法： 对左右子树分别进行递归，返回最小值

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def minDepth(self, root: TreeNode) -> int:
        def helper(root: TreeNode, level:int):
            if not root:
                return inf
            if (not root.left) and (not root.right):
                return level
            return min(helper(root.left, level + 1), helper(root.right, level + 1))
        if not root:
            return 0
        return helper(root, 1)