求最小生成树的Prim算法（数据结构）C语言实现

导论：
1.在连通图中，边若带有权值，则其生成树各边也均带有权值，将生成树各边的权值称为生成树的权。
2.最小生成树：图的生成树最后权值最小的生成树。
3.应用：
可用连通图来表示n个城市及其之间可能设置的通行路线。
其中，网的顶点表示城市，边表示通行路线，权值表示该路线的造价。
想要总造价最低，求最小生成树即可。

栗子：

求该图的最小生成树：（从0开始）
（1） 先找含有顶点0的最小权值边，此时需要考虑的带权边有3条：（0,1）、（0,2）、（0,3），最小权值边为（0,2）；画出（0,2）；

（2） 此时，需要考虑的带权边有6条，分别为（0,1），（0.3），（2.1），（2，3），（2,4），（2,5）；由于（0,2）已经画出，所以不考虑。6条边中最小权值边为（2,5），画出（2,5）；

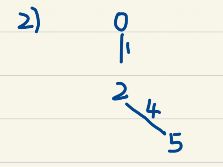
（3） 以此类推

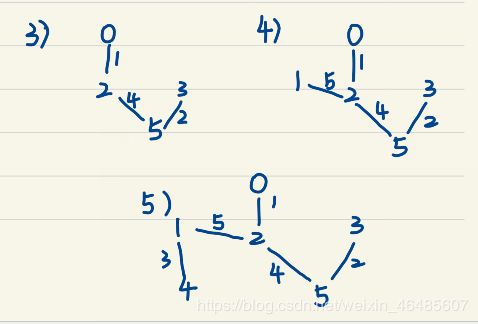
需要注意的是： 在第三步时
已输出顶点为0，2，3，5。
所以此时只需要考虑含有这些顶点且未画出的带权边，即：
（0,1）、（0,3）、（2,1）、（2,3）、（5,4）
此时最小权边为（0,3）、（2,1）、（2,3），权值均为5；分析（0,3），由于0和3均已输出，所以不需要考虑，（2,3）同理。所以此时需要画出的只剩（2,1）；

分析代码：
根据上述连通图的零矩阵有：
… .0 1 2 3 4 5
0–{0,6,1,5,0,0}
1–{6,0,5,0,3,0}
2–{1,5,0,5,6,4}
3–{5,0,5,0,0,2}
4–{0,3,6,0,0,6}
5–{0,0,4,2,6,0}
首先，在考虑第一个顶点0时，只需要考虑含顶点0的的边的权值，即只需要考虑邻接矩阵的第一行。同理，在画出（0,2）后，只需要考虑含有顶点0,2的边的权值，即邻接矩阵的第一、第三行。但，由上述解释中得知，我们在画出（0,2）后是不需要再考虑这条边的，为了避免在遍历第一、第三行的时候边（0,2）的权值的干扰，我们应该在画出（输出）（0,2）之后，将（0,2）在邻接矩阵上**对应的权值初始化为0。**即：

	gm[s][k]=0;
	gm[k][s]=0;

其次， 我们利用 tip数组 来记录某个顶点是否已经画出，初始化tip数组各值为0，若画出，则为1；

再者， 我们借助 min 来找出需要考虑的边之中的最小权值边。同时利用 s和k 记录好最小权值边的位置。找到后，输出，且致tip[s]、tip[k] 为1。表示s和k已经画出。
注意：（如下图）此时，在代码中找最小权值边的时候不会考虑（0,3）和（2,3），因为由代码

	if(tip[i]!=1||tip[j]!=1)
	{	min=gm[i][j];
		s=i;
		k=j;
	}

可知，对于（0,3），tip[0]和tip[3]的值均为1，所以不执行。（2,3）同理。
所以此时找到的最小边仅为（2,1）。（虽然tip[2]的值为1，但tip[1]的值为0，可以执行）。

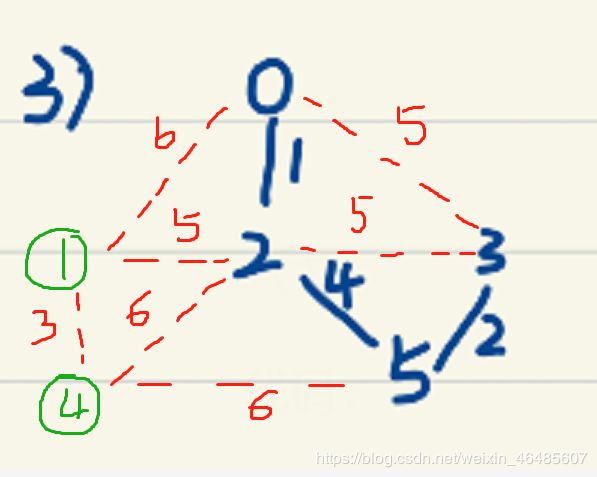
最后， 我们利用 sum 作为判断函数能否结束的标志，在画出第一个顶点0的时候，sum的值为1，在此之后每每画出一个顶点，执行sum++ 。知道sum等于顶点个数n的时候，函数可以结束。

代码：

#include"stdio.h"
#include"stdlib.h"
#define MAXSIZE 77

void xiao(int gm[][6],int n){//最小生成树   n是顶点的个数
	int tip[n+1];//建立数组tip，当生成树中出现了顶点i时，tip[i]就等于1，否则是0 
	int i,j,k,s;
	
	int min;
	int sum=1;//tip为1的个数 
	tip[0]=1;//从顶点0开始求最小生成树，所以顶点0最开始就已画出
	for(i=1;i<n;i++)
		tip[i]=0;
	tip[n]=MAXSIZE;//结束标志 
	do
	{
		min=MAXSIZE;
		for(i=0;i<n;i++)
		{
			if(tip[i]==1)
			{	
				for(j=0;j<n;j++)
				{
					if(gm[i][j]<min&&gm[i][j]!=0)//权值比min小且俩顶点均未曾画出
					{
						if(tip[i]!=1||tip[j]!=1)//i和j至少有一个未曾画出
						{	min=gm[i][j];
							s=i;//用s和k记录最小权值边的位置
							k=j;
						}
					}
				}
			}
		}//找该找的区域的最小权对应的数据 
		
		
		printf("  (%d,%d)---权%d\n",s,k,min);//输出找到的最小权值边
		gm[s][k]=0;
		gm[k][s]=0;//将输出的俩顶点所代表的边初始化，以后不考虑
		tip[s]=1;
		tip[k]=1;//画出俩顶点后，致tip为1，表示已画
		sum++;
	}while(sum<n);//当sum=顶点数n时，求最小生成树操作已完成
}

main(){
	int gm[6][6]={{0,6,1,5,0,0},{6,0,5,0,3,0},{1,5,0,5,6,4},
	{5,0,5,0,0,2},{0,3,6,0,0,6},{0,0,4,2,6,0}};
	xiao(gm,6);
}