数学优化与凸集2（斯坦福凸优化笔记2）

1 仿射和凸集

1 直线和线段

设 x1≠x2 为 Rn 空间中的两个点，那么具有下列形式的点
y=θx1+(1−θ)x2,θ∈R
组成一条穿越 x1 和 x2 的直线。如果 θ∈[0,1] ,就构成了 x1 和 x2 之间的闭线段。

2 仿射集合
如果通过集合 C⊆R 中任意两个不同点的直线仍在集合中，那么集合 C 是仿射的。
这个概念可以扩展到多个点的状况，如果 θ1+⋯+θk=1 ，我们称具有 θ1x1+⋯+θkxk 形式的点为 x1,⋯xk 的仿射组合。
根据仿射集合的定义，如果 C 是一个仿射集合， x1,⋯xk∈C ,且 θ1+⋯+θk=1 ，那么 θ1x1+⋯+θkxk 仍然在 C 中。

3 凸集
集合 C 被称为凸集，如果 C 中任意两点间的线段都在 C 中，即对于任意 x1,x2∈C 和满足 0≤θ≤1 的 θ 都有
θx1+(1−θ)x2∈C
简单的可以理解成，集合中任意两个点之间的路径都包含在集合里。
集合中所有点的凸组合的集合叫做凸包，记 conv C
conv C={θ1x1+⋯+θkxk∣xi∈C,θi≥0,i=1,⋯,k,θ1+⋯+θk=1}
凸包是包含 C 最小的凸集。

上图是凸包的图片（图片来自斯坦福Boyd Convex Optimization）
左图为一些点的凸包，右图为肾型的凸包。
4 锥

对于任意 x∈C 和 θ≥0 都有 θx∈C ,我们称集合 C 为锥或者非负齐次。
锥可以直观的理解为从原点到各个点的辐射的直线组成的集合。

上图的三条直线可以认为是锥，对于任意直线上点 x1,x2,x3 来说，满足上述锥的定义。
如果集合 C 是锥，并且是凸的，即对于任意 x1.x2∈C 和 θ1,θ2≥0 有：
θ1x1+θ2x2∈C
此时这个集合既是一个锥，又是凸的，称为凸锥。
在二维上，凸锥构成了二维的扇形。

（图片来自斯坦福Boyd Convex Optimization）
集合 C 的锥包是 C 中所有元素的锥组合的集合。即
{θ1x1+⋯+θkxk∣xi∈C,θi≥0,i=1,⋯,k},
这是包含 C 最小的凸锥。

（图片来自斯坦福Boyd Convex Optimization）

2 一些常见的凸集

下面介绍一些常用的凸集，这些凸集将在以后经常用到。

1超平面与半空间
超平面是有以下形式的集合：
{x∣aTx=b}
其中： a∈Rn,a≠0 且 b∈R 。
从几何上讲，我们可以理解为超平面法线方向为 a ,常数 b∈R 决定了超平面到原点的偏移。超平面将 Rn 划分成两个半空间。半空间是具有下列形式的集合：
{x∣aTx≤b}
超平面既是凸的，又是仿射的；

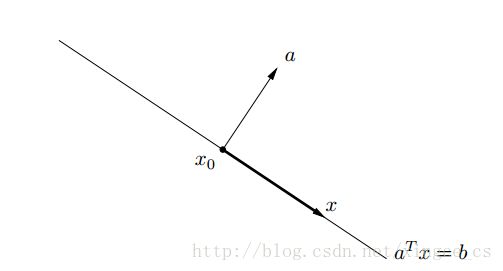
（图片来自斯坦福Boyd Convex Optimization）
半空间是凸的。

（图片来自斯坦福Boyd Convex Optimization）

2 Euclid 球和椭球

Rn 空间中的Euclid 球（简称球）形式如下：
B(xc,r)={x∣∥x−xc∥2≤r}={x∣(x−xc)T(x−xc)≤r2}
还可以表达为：
B(xc,r)={xc+ru∣∥u∥2≤1}
另一类相关的凸集是椭球：
ε={(x−xc)TP−1(x−xc)≤1}
椭球的另外一种常见的表示形式是：
ε={xc+Au∣∥u∥2≤1}
其中 A 是非奇异的方阵，我们一般假设 A 对称正定，且 A=P−1 ,这时此表示方式和上一种表示方式一致。
球和椭球都是凸的。

3 范数球和范数锥

范数球可以如下定义，设 ∥⋅∥ 是 Rn 中的范数，则范数球：
{x∣∥x−xc∥≤r}
范数球是上面Euclid球的推广，同样是凸的。

范数锥的定义如下：
C={(x,t)∣∥x∥≤t}⊆Rn+1

范数锥是个凸锥。

这个图是二维 {∥x∥max≤t} 的图片。

这个图是二维 {∥x∥1≤t} 的图片。

4 多面体

多面体定义为有限个线性等式和不等式的解集：

P={x∣aTjx≤bj,j=1,⋯,m, cTjx=dj,j=,⋯,p}
多面体是有限个半空间和超平面的交集。多面体是一个凸集。

多面体还可以表示为：
P={x∣Ax⪯b,Cx=d}
其中：

A=⎡⎣⎢⎢⎢aT1⋮aTm⎤⎦⎥⎥⎥, C=⎡⎣⎢⎢⎢cT1⋮cTp⎤⎦⎥⎥⎥,

5 半正定锥

我们用 Sn 表示对称 n×n 矩阵的集合，这个集合是一个维数为n(n+1)/2的向量空间。我们用 Sn+ 表示对称半正定矩阵的集合
Sn+={X∈Sn∣X⪰0}
用 Sn++={X∈Sn∣X≻0} 表示对称正定矩阵的集合。 Sn+ 和 Sn++ 集合都是凸锥。
(未完，待续)