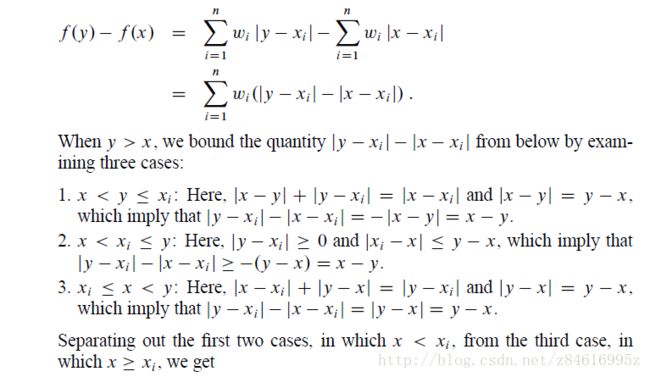算法导论第九章课后答案

9.1-1 证明：在最坏情况下，找到n个元素中第二小的元素需要n+向上取整lgn-2次比较。

我们对于查找第2小元素分成2步。
step1:我们先将数组中的元素两两成对比较，共需n/2次比较，那么就有n/2个元素是较小的元素，然后再将这些较小的元素再次两两成对比较，又淘汰一半，重复这样的循环，每次淘汰一半元素直到只剩下1个元素，该元素就是最小元素。经过的比较次数为S=n/2+n/4+...(n/(2^k)=1) k=lgn S=n-1次。
step2:经过以上比较，就形成了一个二叉树，那么第2小的元素肯定与最小元素比较过，所以我们采取的方法是，从根结点也就是最小元素开始沿着根向叶子结点开始查找等于根节点的子结点A，第二小的元素就应该在与A结点属于同一个父结点的另外一个子结点B上，将B结点上的值给予第二小元素second，这样经过以上方式最坏lgn-1次比较，只要小于second值的元素，second就被覆盖成该元素，最终总能找到第2小元素。所以总比较次数为n-1+lgn-1=n+lgn-2。但是具体实现我还未想出来。

9.1-2 证明：在最坏情况下，同时找到n个元素中最大值和最小值的比较次数的下界是向上取整3n/2-2

我们将输入元素两两相互进行比较，然后把较小的与当前最小值比较，较大的与当前最大值比较，所以2个元素每次循环要比较3次，但是仅仅需要进行n/2次循环，所以总的比较次数为(向上取整)3n/2-2次。

以下是代码：

//同时求最小与最大值，只需要3n/2次比较
#include 
#include 
using namespace std;
const n=10;
void max_min(int A[],int &max,int &min)//同时找出最大值和最小值。
{
    for (int i=0;iA[i+1])
        {
            if (A[i]>max)
            {
                max=A[i];
            }
            if (A[i+1]max)
            {
                max=A[i+1];
            }
            if (A[i]A[1])
        {
            max=A[0];min=A[1];
        }
        else
        {
            max=A[1];min=A[0];
        }
    }
    //求数组A的max与min
    max_min(A,max,min);
    //输出max与min
    cout<<"max="<9.2节代码：
 
  
 
  
#include 
#include 
using namespace std;
const n=8;
int PARTITION(int A[],int p,int r);
int RANDOM(int p,int r)
{
    int t=rand()%(r-p+1)+p;
    return t;
}
int RANDOMIZED_PARTITION(int A[],int p,int r)
{
    int i=RANDOM(p,r);
    swap(A[r],A[i]);
    return PARTITION(A,p,r);
}
int PARTITION(int A[],int p,int r)
{
    int x=A[r];
    int i=p-1;
    for (int j=p;j<=r-1;j++)//O(n)
    {
        if (A[j]<=x)
        {
            i++;
            swap(A[i],A[j]);
        }
    }
    swap(A[i+1],A[r]);
    return i+1;
}
int RANDOMIZED_SELECT(int A[],int p,int r,int i)
{
    if (p==r)
    {
        return A[p];
    }
    int q=RANDOMIZED_PARTITION(A,p,r);
    int k=q-p+1;
    if (i==k)
    {
        return A[q];
    }
    else if(i
 
  
 
  
9.2-1 证明：在RANDOMIZED-SELECT中，对长度为0的数组，不会进行递归调用。
 
  
看上面的代码，从RANDOMIZED-SELECT函数知，长度为0的数组 p=r，那么直接返回A[p].不做下面的随机划分和递归调用。
 
  
9.2-2 证明：指示器随机变量Xk和T(max(k-1,n-k))是独立的。
 
  
因为我们最初假设输入数组各个元素是互异的，所以有证明结论。
 
  
9.2-3 给出RANDOMIZED-SELECT的一个基于循环的版本。
 
  
 
  
int RANDOMIZED_SELECT(int A[],int p,int r,int i)
{
    while (1)
    {
        if (p==r)
        {
            return A[p];
        }
        int q=RANDOMIZED_PARTITION(A,p,r);
        int k=q-p+1;
        if (i==k)
        {
            return A[q];
        }
        else if(i
 
  
 
  
 
  
 
  9.2-4 假设用RANDOMIZED-SELECT去选择数组Α={3,2,9,0,7,5,4,8,6,1}的最小元素，给出能够导致RANDOMIZED-SELECT最坏情况发生的一个划分序列。 
  
 
  
每次都选择最大元素作为划分主元，这样就有T(n)=T(0)+T(n-1)+O(n)产生最坏运行时间。
 
  
9.3 最坏情况为线性时间的选择算法 
 
  
由于书上没有给出代码，经过我研究代码可以这么写，当然对于第3步递归调用SELECT以找到中位数的中位数，不知道怎么实现，所以我就在插入排序函数中对中位数辅助数组B进行排序以便求出中位数的中位数x
 
  
9.3最坏情况为线性时间的选择算法的代码
 
  
9.3-1在算法SELECT中，输入元素被分为每组5个元素。如果它们被分为每组7个元素，该算法仍然会是线性时间吗？证明：如果分成每组3个元素，SELECT的运行时间不是线性的。
 
  
当被划分为每组7个元素时，类似书中分析有至少有一半大于等于中位数的中位数x，因此在Ceil(n/7)个组中，除了那个所含元素可能少于7的组合包含x的2那个组外，至少有一半的组有4个元素大于x，不计这两个组，大于x元素个数至少为4(Ceil((1/2)Ceil(n/7))-2)≥2n/7-8,类似小于x的元素至少有2n/7-8个，那么最多有5n/7+8元素递归调用SELECT。T(n)≤T(n/7)+T(5n/7+8)+Ο(n),假设有线性时间T(n)≤cn，那么用代换法，T(n)≤cn/7+5nc/7+8c+an=cn+(-nc/7+8c+an) 只要-nc/7+8c+an≤0即可，那么当n≥112时，我们选择c≥14a，T(n)=Ο(n),当n≤112，有T(n)=Θ(1).
 当被划分为每组3个元素时，类似上面分析有2(Ceil((1/2)Ceil(n/3))-2)≥n/3-4,至少有2n/3+4个元素参与递归。T(n)≤T(n/3)+T(2n/3+4)+Ο(n)假设T(n)≤cn也有线性时间，则T(n)≤cn+4c+an,由于我们假设的这两个常数是＞0的，所以4c+an无论如何也不可能＜0，所以T(n)≠Ο(n)。所以被划分为3个元素就无法在线性时间内完成选择。所以有此我们知划分最低是5个一组。
 
  
9.3-2分析SELECT，并证明：如果n≥140，则至少ceil(n/4)个元素大于中位数的中位数x,至少ceil(n/4)个元素小于x？
 
  
由书中知：当n≥140时，3(Ceil((1/2)Ceil(n/5))-2)≥3n/10-6≥2.5n/10+1=n/4+1≥Ceil(n/4),所以至少有Ceil(n/4)个元素大于中位数的中位数
 x同理，由书中知，有多少大于x的数，就有多少小于x的数。
 
  
9.3-3 假设所有元素都是互异的，说明在最坏情况下，如何才能使快速排序的运行时间为Ο(nlgn)?
 
  
最坏情况快速排序运行时间为O(nlgn)算法
 
  
9.3-4 假设对一个含有n个元素的集合，某算法只用比较来确定第i小的元素。证明：无需另外的比较操作，它也能找到比i小的i-1个元素和比i大的n-i个元素。
 
  
因为在SELECT函数查找第i个元素时，不断的以辅助中位数数组的中位数x为主元进行划分。必然大于主元x的在右边，小于主元x的在左边。x就是第k小的元素，当待查找元素i=k时，则返回x。如果i≠k，那么继续递归。所以只要找到了第i小元素，那么就会以这个元素作为主元对整个数组进行划分，低区的i-1个元素肯定都是小于主元的，高区n-i个元素肯定都是大于主元的。
 
  
9.3-5 假设已经有了一个用于求解中位数的“黑箱”子程序，它在最坏情况下需要线性运行时间。写出一个能解决任意顺序统计量的选择问题的线性时间算法。
 
  
请看链接处find函数代表查找中位数子程序SELECT函数代表能解决任意统计量的选择问题线性算法
 
  
9.3-6 对一个含有n个元素的集合来说，所谓k分位数（the kth quantile），就是能把已排序的集合分成k个大小相等的集合的k-1个顺序统计量。给出一个能输出某一集合的这k-1个顺序统计量的O(nlgk)时间的算法。
 
  
9.3-6求k分位数
 
  
9.3-7 给出一个O(n)时间的算法，在给定一个有n个不同数字的集合S以及一个正整数k≤n后，它能确定出S中最接近其中位数的k个数
 
  
线性时间查找最接近中位数的k个数
 
  
9.3-8 设 x[1..n]和Y[1..n]为两个数组，每个都包含n个已排序的数。给出一个求数组X和Y中所有2n个元素的中位数的O(lgn)时间的算法。
 
  
O(lgn)时间内求出两个已排序数组的中位数
 
  
9.3-9 Olay教授是一家石油公司的顾问。这家公司正在计划建造一条从东向西的大型输油管道，这一管道将穿越一个有n口油井的油田。公司希望有一条管道支线沿着最短路径从每口油井链接到主管道（方向或南或北），给定每口油井的x和y坐标，教授应该如何选择主管道的最优位置，使得各支线的总长度最小？证明：该最优位置可以在线性时间内确定。
 
  
设x代表东西向的横坐标，y代表南北向的纵坐标。主管道坐标(x,y)，主管道与支线管道的最短距离d=√(xi-x)^2+(yi-y)^2，由于是最短距离，那么xi=x。也就是di=|yi-y| 。总的距离
 
  
d=∑di=∑|yi-y|。要使d最小，那么需要求出数组yi中位数。当n为奇数，那么中位数很容易求得。当n为偶数，那么就是求n/2与n/2+1之间的值。
 
  
如何证明呢？ 我们可以用到书中最坏线性时间求第i小元素的方法来求y1,y2..yn这n个数的中位数。最坏线性时间求第i小元素已经在此链接给出
 
  
 
  
 
  
 9-1 (有序序列中的i个最大数) 给定一个包含n个元素的集合，我们希望利用基于比较的算法找出按顺序排列的前i个最大元素。请设计能实现下列每一项要求，并且具有最佳渐近最坏情况运行时间的算法，以n和i来表示算法的运行时间：
 
  
 a.对输入数据排序，并找出前i个最大数。
 
  
    用归并排序和堆排序，根据9.3-3结论，其实也可以用快速排序。（这三种排序算法时间复杂度均为O(nlgn+i)(三种排序+循环输出i次前i个最大元素)=O(nlgn)）
 
  
 b.对输入数据建立一个最大优先队列，并调用EXTRACT-MAX过程i次。
 
  
    用堆排序即可。时间复杂度为O(n+ilgn)(建堆+连续i次调用EXTRACT-MAX函数)。
 
  
 c.利用一个顺序统计量算法来找到第i大的元素，然后用它作为主元划分输入数组，再对前i大的数排序。
 
  
   step1：9.3节给出的最坏线性时间的选择SELECT函数找出第i大的元素。 O(n)
   step2：快速排序中的对主元划分的PARTITION函数。划分后，大于第i个元素的在右边，小于第i个元素的在左边。O(n)
   step3: 对右边大于第i个元素的i个数用a)的那三种方法进行排序。O(ilgi)
 所以总时间复杂度O(n+ilgi)。
 
  
 
 
  
 
 
  
 a)先将这n个元素按照升序排列，前面n/2个元素xi<=xk(i=1,2...n/2 xk为中位数)它们的权重wi=1/n.所以∑wi≤(n/2)(1/n)=1/2。同理对于后
 面n/2个元素也有∑wi≤(n/2)(1/n)=1/2，xk既为中位数也为带权中位数。
 b)利用时间为O(nlgn)排序算法得到一个有序数组，按照顺序依次循环O(n)次求和直到满足带权中位数所给公式即可。
 c)step 1:按照9.3节SELECT函数找主元的方法找到主元。
   step 2:以这个主元为中枢对数组进行划分PARTITION函数操作。结果是小于主元的在左边，大于的在右边。
   step 3:计算以主元为中枢的左右两半部分的权重和，是否满足题目中的权重公式。
   step 4：如果满足，就返回这个主元。
   step 5：如果不满足，就递归本算法进行step 1234操作。如果左半部分大于1/2，就对大于1/2左半部分进行递归直到左半部分刚好小于1/2
 为止，如果右半部分大于1/2，就对右边进行递归直到右半部分小于1/2为止。
 对于权重的计算公式不太清楚。所以我不知道如何将xi转换为xi的权重值wi,所以在此仅写出思路。
 d)网上的答案和《教师手册》的解答，是我没看懂？，还是本身就经不起推敲？《教师手册》里分两种情况讨论，而每种情况又有三个分支情况但是三个分支情况讨论完后，直接分离出了两种不符合题意的情况，而没有说明原因，所以我很费解。请看具体截图。
 
  
 
 
  
 
 
  
 其中Separating out（分离出12种情况的原因是什么？）y 
  
 但是只说明了 t+1的情况，虽然t+1的情况很容易看明白。但是上面说t+1就能代表一般情况了，这我就不敢苟同了,我在推测t+2...t+x时没有推出和t+1一样的结论，所以感觉这个网页给出的证明不具一般性。
 
  
 e)利用d)的结论，对横坐标x与纵坐标y分别求带权中位数，即可求出最短距离。
 
  
 
  
    这个问题我没有看懂。如果就像提示所说，将n/2对元素两两比较，较小的放入到一个集合中这样递归后就可以得出第i小元素，但是我在实际写代码的时候发现，要想把数组前n/2个元素放入到较小的那一组，很困难！为什么呢？如果不用PARTION函数以中位数将数组划分为小的一组，大的一组（如果用中位数来划分，那么必然一开始就调用了SELECT函数，这样再进行查找显得没必要，因为不能减少比较次数！），而用其他方式我发现，在进行比较的一对元素中，可能这对元素都比较小，（比如一个数组有12个数，输出第5小的元素，那么我成对比较时，第4小和第5小的元素刚好为一对进行比较了，那么必须舍弃其中一个元素（不幸的是刚好舍弃了第5小的元素），而经过比较，较小的新数组中，恰好没有第5小元素，那么在这个新数组中如果经过数次递归已经不能再递归后，需要掉用SELECT函数进行查找，无论如何也找不到第5小的元素了，第5小的已经被放入较大的那一组了。）
 
  
    最后总结2个问题：1，需要查找的第i小元素刚好分入到较大的那一组，无论如何也不能在较小的那一组找到这个元素了。
 
  
                                    2，在递归的成对比较舍弃较大的元素时，比较的这两个元素刚好是数组前i小元素里面的两个元素，那么舍弃了一个后，如何调整最后的SELECT函数查找的第x小元素的x值？这也是个问题。如何有大牛知道如何解决这两个问题请留言哦。
 
  
9-4 待解决。
 
  
这道题是第三版新增的题，题目全是数学概率题。