前言
如果你在考提高组的前一天还对这有疑问，那你会与一等奖失之交臂;
如果你还在冲击普及组一等奖，那这篇博客会浪费你人生中宝贵的5～20分钟。
（这句话摘自Dijkstra_Liu的blog ）
概念
树状数组(Binary Indexed Tree(B.I.T),Fenwick Tree)是一个查询和修改都为log(n)的基于倍增思想数据结构（数组）。
树状数组和线段树很像，但能用树状数组解决的问题，基本上都能用线段树解决，而线段树能解决的树状数组不一定能解决。
但相比较而言，树状数组效率要高很多，所以在某些题来说，树状数组是不二之选。
结构
在oi-wiki上的图，
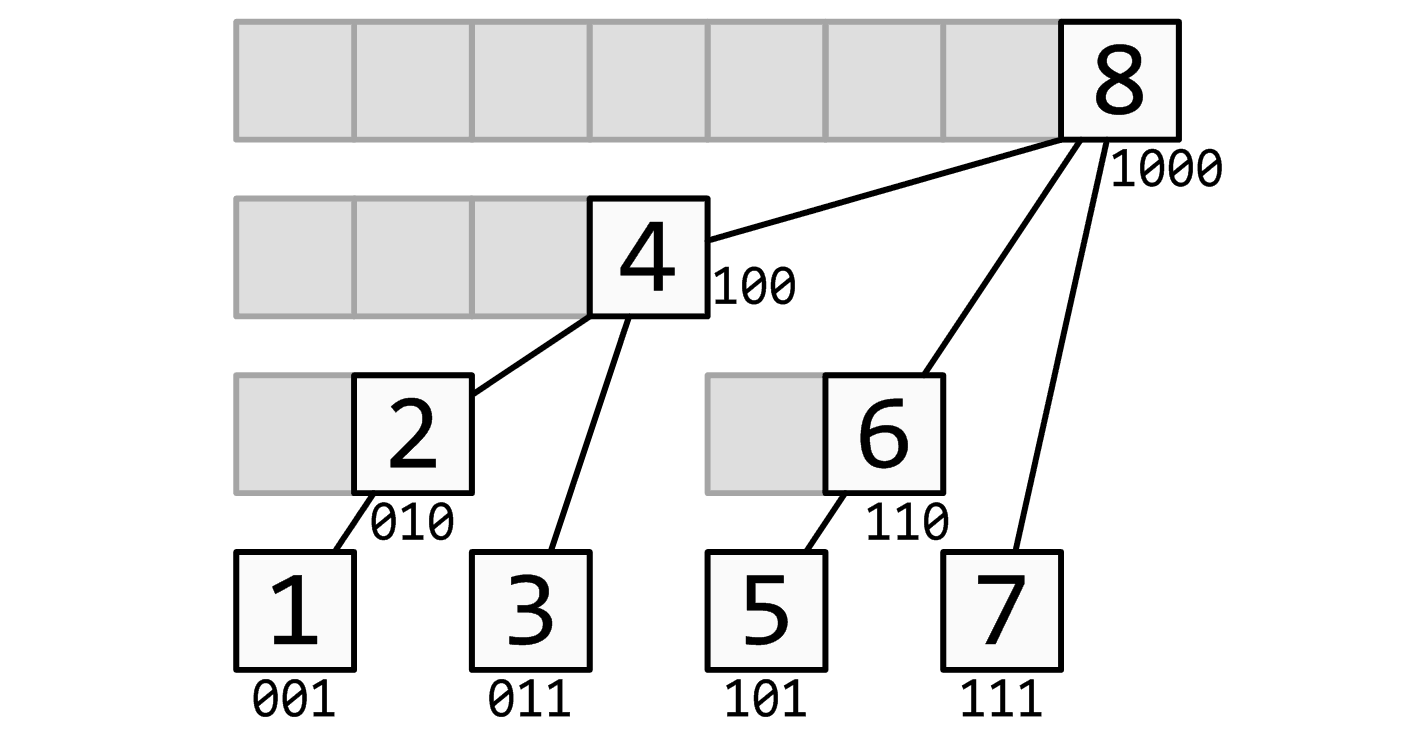
思想和线段树有些类似：用一个大节点表示一些小节点的信息，进行查询的时候只需要查询一些大节点而不是更多的小节点。
我们假设父亲节点表示它子子孙孙的节点。
列表：
| 点 | 代表 | 个数 |
|---|---|---|
| 1(0001) | 1 | 1 |
| 2(0010) | 1 ， 2 | 2 |
| 3(0011) | 3 | 1 |
| 4(0100) | 1 ， 2 ， 3 ， 4 | 4 |
| 5(0101) | 5 | 1 |
| 6(0110) | 5 ， 6 | 2 |
| 7(0111) | 7 | 1 |
| 8(1000) | 1 ， 2 ， 3 ， 4 ， 5 ， 6 ， 7 ， 8 | 8 |
这里引入一个新函数lowbit(x)，即算出x二进制的从右往左出现第一个1以及这个1之后的那些0组成数的二进制对应的十进制的数。
我们不难发现，一个点的代表个数为lowbit(x)。
证明：
对于一个x个点，
\[x=a_0*2^0+a_1*2^1+\ldots+a_{upbit(x)}*2^{upbit(x)} \qquad (a_{n}=1 \mid a_{n}=0) \]
在第x个点之前，其必有
x-lowbit(x)个点被包含（如上图）。
所以，第x个点包含lowbit(x)个点。
至于lowbit()的实现，我们可以用x&-x。
证明：
你自己推去吧，这里给例子。
例如22，x=10110，~x=01001，~x+1=01010=-x，x&-x=10110&01010=10
lowbit(22)=2
有了x&-x，我们就可以用O(logn)的复杂度来查询整个数组。
一维功能
单点修改，区间查询
\[sum[x]=\sum_{i=1}^{x}a[i] \]
/*O(logn)*/
int t[N];//树状数组
void Add(int x,int d)//在第x位加上d
{
for(;x<=n;x+=(x&-x) t[x]+=d;
}
int Ask(int x)//询问前x项的和
{
int ans=0;
for(;x;x-=(x&-x)) ans+=t[x];
return ans;
}
Ask(r)-Ask(l-1)//询问[l,r]
luogu模板
AC code
P3374
#include
#include
#include
#include
using namespace std;
const int N=5e5+5;
int n,m,c[N];
void Add(int x,int d)
{
for(;x<=n;x+=(x&-x)) c[x]+=d;
}
int Quest(int x)
{
int re=0;
for(;x;x-=(x&-x)) re+=c[x];
return re;
}
void Solve()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
{ int a;scanf("%d",&a);Add(i,a); }
for(int i=1;i<=m;++i)
{
int s,a,b;scanf("%d%d%d",&s,&a,&b);
if(s==1)
Add(a,b);
else
printf("%d\n",Quest(max(b,a))-Quest(min(a,b)-1));
}
}
int main()
{
Solve();
return 0;
}
区间修改，单点查询
通过差分（就是记录数组中每个元素与前一个元素的差），把问题转化为单点修改，区间查询。
z[i]为i与i-1的差分
查询\(a[x]=/sum_i=1^xz[i]\)
修改[l,r]+d,即为z[l]+=d,z[r+1]-=d;
/*O(logn)*/
int t[N];
void Add(int x,int d)
{
for(;x<=n;x+=(x&-x)) t[x]+=d;
}
int Ask(int x)
{
int ans=0;
for(;x;x-=(x&-x)) ans+=t[x];
return ans;
}
Add(l,d),Add(r+1,-d);//修改[l,r]+d
luogu模板
AC code
//P3368
#include
#include
#include
#include
using namespace std;
const int N=5e5+5;
int n,m,c[N],a[N];
void Add(int x,int d)
{
for(;x<=n;x+=(x&-x)) c[x]+=d;
}
int Quest(int x)
{
int re=0;
for(;x;x-=(x&-x)) re+=c[x];
return re;
}
void Solve()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;++i)
{ scanf("%d",a+i);Add(i,a[i]-a[i-1]); }
for(int i=1;i<=m;++i)
{
int s;scanf("%d",&s);
if(s==1)
{
int a,b,c;scanf("%d%d%d",&a,&b,&c);
Add(a,c);Add(b+1,-c);
}
else
{
int a;scanf("%d",&a);
printf("%d\n",Quest(a));
}
}
}
int main()
{
Solve();
return 0;
}
区间修改，区间查询
基于区间修改，单点查询的差分，z[i]为i与i-1的差分。
\[\begin{align*} & \sum_{i=1}^{x}a[i] \\ & = \sum_{i=1}^{x}\sum_{j=1}^{i}z[j] \\ & = \sum_{i=1}^{x}z[j]*(x-i+1) \\ & = (x+1)*\sum_{i=1}^{x}z[i]-\sum_{i=1}^{x}z[i]*i \\ \end{align*} \]
然后，我们可以维护两个数组的前缀和：
一个是\(t[i]=\sum_{j=1}^{i}z[j]\)
另一个是\(tr[i]=\sum_{j=1}^{i}z[j]*j\)
/*O((logn)^2)*/
int t[N],tr[N];
void Add(int x,int d)
{
for(int i=x;i<=n;i+=(i&-i))
t[i]+=d,tr[i]+=d*x;
}
int Ask(int x)
{
int ans=0;
for(int i=x;i;i-=(i&-i))
ans+=(x+1)*t[i]-tr[i];
return ans;
}
Add(l,d),Add(r+1,d);//修改[l,r]+d;
Ask(r)-Ask(l-1);//查询[l,r];
luogu模板
AC code
//P2357
#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=2e5+5;
ll n,m,c[N],c0[N];
void Add(ll x,ll d)
{
for(ll i=x;i<=n;i+=(i&-i))
c[i]+=d,c0[i]+=x*d;
}
ll ask(ll x)
{
ll re=0;
for(ll i=x;i;i-=(i&-i))
re+=(x+1)*c[i]-c0[i];
return re;
}
void Solve()
{
scanf("%lld%lld",&n,&m);
int now,last=0;
for(int i=1;i<=n;++i)
{
scanf("%d",&now);
Add(i,now-last);
last=now;
}
for(int i=1;i<=m;++i)
{
ll s;scanf("%lld",&s);
if(s==1)
{
ll a,b,c;scanf("%lld%lld%lld",&a,&b,&c);
Add(a,c);Add(b+1,-c);
}
else if(s==2)
{
ll a;scanf("%lld",&a);
Add(1,a);Add(2,-a);
}
else if(s==3)
{
ll a;scanf("%lld",&a);
Add(1,-a);Add(2,a);
}
else if(s==4)
{
ll a,b;scanf("%lld%lld",&a,&b);
printf("%lld\n",ask(max(a,b))-ask(min(a,b)-1));
}
else
{
printf("%lld\n",c[1]);
}
}
}
int main()
{
Solve();
return 0;
}
二维功能
单点修改，区间查询
\[sum[x][y]=\sum_{i=1}^{x}\sum_{j=1}^{y}a[i][j] \]
/*O(logn*longn)*/
int t[N][N];
void Add(int x,int y,int d)
{
for(;x<=n;x+=(x&-x))
for(int i=y;i<=n;i+=(i&-i))
t[x][i]+=d;
}
int Ask(int x,int y)
{
int ans=0;
for(;x;x-=(x&-x))
for(int i=y;i<=n;i-=(i&-i)
ans+=t[i][j];
return ans;
}
Ask(x,y)+Ask(a-1,b-1)-Ask(x,a-1)-Ask(b-1,y);//查询[a,b]~[x][y] (a<=x&&b<=y)
区间修改，单点查询
因为二维前缀和为
\[sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j] \]
所以设z[i][j]为a[i][j]与a[i-1][j]+a[i][j-1]-a[i-1][j-1]的差。
例如：
a[i][j]
1 4 5 6 3
2 5 3 7 8
9 4 5 6 2
1 4 7 6 9
1 2 3 6 1
z[i][j]
1 3 1 1 -3
1 0 -3 3 4
7 -8 3 -3 -5
-8 8 2 -2 7
0 -2 -2 4 -8
当我们想把中间的3×3加上d时，差分变化为:
z[i][j]
0 00 0 0 00
0 +d 0 0 -d
0 00 0 0 00
0 00 0 0 00
0 -d 0 0 +d
实际变化为:
a[i][j]
0 0 0 0 0
0 d d d 0
0 d d d 0
0 d d d 0
0 0 0 0 0
查询\(\sum_{i=1}^{x}\sum_{j=1}^{y}z[i][j]\)
修改z[a][b]+=d,z[a][y+1]-=d,z[x+1][b]-=d,z[x+1][y+1]+=d; (a<=x&&b<=y)
/*O((logn)^2)*/
int t[N][N];
void Add(int x,int y,int d)
{
for(;x<=n;x+=(x&-x))
for(int i=y;i<=n;i+=(i&-i))
t[x][i]+=d;
}
void Ask(int x,int y)
{
int ans=0;
for(;x;x-=(x&-x))
for(int i=y;i;i-=(i&-i))
ans+=t[x][i];
return ans;
}
Add(a,b,d),Add(a,y+1,-d),Add(x+1,b,-d),Add(x+1,y+1,d);//修改[a,b]~[x,y]+d (a<=x&&b<=y)
区间修改，区间查询
\[\begin{align*} & \sum_{i=1}^{x}\sum_{j=1}^{y}\sum_{q=1}^{i}\sum_{w=1}^{j}z[q][w] \\ & = \sum_{i=1}^{x}\sum_{j=1}^{y}z[i][j]*(x-i+1)*(y-j+1) \\ & = \\ & (x+1)*(y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}z[i][j] \\ & -(y+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}z[i][j]*i \\ & -(x+1)*\sum_{i=1}^{x}\sum_{j=1}^{y}z[i][j]*j \\ & +\sum_{i=1}^{x}\sum_{j=1}^{y}z[i][j]*i*j \end{align*} \]
所以要开四个数组维护：
t[i][j]维护z[i][j]
ti[i][j]维护z[i][j]*i
tj[i][j]维护z[i][j]*j
tij[i][j]维护z[i][j]*i*j
/*O((logn)^2)*/
int t[N][N],ti[N][N],tj[N][N],tij[N][N];
void Add(int x,int y,int d)
{
for(int i=x;i<=n;i+=(i&-i))
for(int j=y;j<=n;j+=(j&-j))
t[i][j]+=d,ti[i][j]+=d*x,tj[i][j]+=d*y,tij[i][j]+=d*i*j;
}
int Ask(int x,int y)
{
int ans=0;
for(int i=x;i;i-=(i&-i))
for(int j=y;j;j-=(j&-j))
ans+=(x+1)*(y+1)*t[i][j]-(y+1)*ti[i][j]-(x+1)*tj[i][j]+tij[i][j];
return ans;
}
Add(a,b,d),Add(a,y+1,-d),Add(x+1,b,-d),Add(x+1,y+1,d);//修改[a,b]~[x,y]+d (a<=x&&b<=y)
Ask(x,y)+Ask(a-1,b-1)-Ask(x,a-1)-Ask(b-1,y);//查询[a,b]~[x][y] (a<=x&&b<=y)
拓展功能
不可修改，最大最小
树状数组还可以求一个数组的区间中的最大最小。
/*O(logn)*/
int tmax[N],tmin[N],a[N];
memset(tmax,0x80,sizeof(tmax));
memset(tmin,0x3f,sizeof(tmin));
void Add(int x,int d)
{
for(;x<=n;x+=(x&-x))
tmax[x]=max(tmax[x],d),tmin[x]=min(tmin[x],d);
}
递归版本
/*O(logn)*/
int Fmax(int l,int r)
{
if(l>=r) return a[l];
if(r-(r&-r)+1>=l) return max(tmax[r],Fmax(l,r-(r&-r)));
else return max(a[r],Fmax(l,r-1));
}
int Fmin(int l,int r)
{
if(l>=r) return a[l];
if(r-(r&-r)+1>=l) return min(tmin[r],Fmin(l,r-(r&-r));
else return min(a[r],Fmin(l,r-1));
}
递推版本
/*O(logn)*/
int Fmax(int l,int r)
{
int ans=0;
while(l<=r)
{
if(r-(r&-r)+1>=l) ans=max(ans,tmax[r]),r-=(r&-r);
else ans=max(ans,a[r]),--r;
}
return ans;
}
int Fmin(int l,int r)
{
int ans=0;
while(l<=r)
{
if(r-(r&-r)+1>=l) ans=min(ans,tmin[r]),r-=(r&-r);
else ans=min(ans,a[r]),--r;
}
return ans;
}
经验证明递推比递归快，不信可以试试这题，记得用树状数组写。
AC code
//P3865
#include
#include
#include
#include
using namespace std;
const int N=1e5+5;
int n,m,a[N],cmax[N];
char S[1<<20], * p1, * p2;
char gc()
{
if(p1==p2)
{
p1=S;
p2=S+fread(S,1,1<<20,stdin);
}
return *p1++;
}
inline int read()
{
int s = 0, w = 1;
char ch = gc();
while(ch < '0' || ch > '9') {if(ch == '-') w = -1; ch = gc();}
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = gc();
return s * w;
}
inline int Fmax(int l,int r)
{
int ans=0;
while(l<=r)
{
if(r-(r&-r)+1>=l) ans=max(ans,cmax[r]),r=r-(r&-r);
else ans=max(ans,a[r]),r-=1;
}
return ans;
}
void Solve()
{
n=read(),m=read();
for(register int i=1;i<=n;++i)
{
a[i]=read();
cmax[i]=max(cmax[i],a[i]);
if(i+(i&-i)<=n)cmax[i+(i&-i)]=cmax[i+(i&-i)]>cmax[i] ? cmax[i+(i&-i)] : cmax[i];
}
for(register int i=1;i<=m;++i)
{
int a=read(),b=read();
printf("%d",Fmax(a,b));
printf("\n");
}
}
int main()
{
Solve();
return 0;
}
区间固定，第k大小
将所有数字看成一个可重集合，即定义数组t[]表示值为x的元素在整个序列重出现了t[x]次。找第k大就是找到最大的x恰好满足\(\sum_{i=1}^xa[i]
因为在树状数组的结构中，节点是以2的幂的长度划分的，所以我们可以每次扩展2的幂的长度来化简复杂度。
最后注意第k大小要加1。
这里只列举第k小，因为第k大为第n-k小。
/*O(logn)*/
int t[N];
void Add(int x,int d)
{
for(x<=n;x+=(x&-x))t[x]+=d;
}
int Findk(int k)
{
int ans=0,now=0;
for(int i=log2(maxn);i>=0;--i)
{
ans+=(1<tot||now+t[ans]>=k) ans-=(1< luogu例题
AC code
//P1168
#include
#include
#include
#include
typedef long long ll;
using namespace std;
const int N=1e5+5;
int n,m,c[N],a[N],b[N],tot;
void Add(int x,int d)
{
for(;x<=n;x+=(x&-x)) c[x]+=d;
}
int Findk(int k)
{
int ans=0,now=0;
for(int i=log2(n);i>=0;--i)
{
ans+=(1<
tot||now+c[ans]>=k) ans-=(1<
>1)]);
}
}
int main ()
{
Solve();
return 0;
}
离散化后，带权数组
有的时候，我们需要用数值做下标，解决这样的问题就是离散化，也就成了带权树状数组。
这使空间复杂度由T(maxn)变为T(tot)。
/*O(nlogn)*/
int n,tot,m[N],a[N];
scanf("%d",&n);
for(int i=1;i<=n;++i)
scanf("%d",&a[i]),m[i]=a[i];
sort(a+1,a+1+n);
tot=unique(a+1,a+n+1)-a-1;//去重
for(int i=1;i<=n;++i)
m[i]=lower_bound(a+1,a+tot+1,m[i])-a;
例如：
a[]
1 2 3 10000
m[]
1 2 3 4
luogu例题
AC code
//P1168
以为没有？其实和上次是一个题。
结合动规，数组优化
树状数组给动规优化，可使O(n)变为O(logn)。
以最长子序列为例：
/*O(nlogn)*/
int f[N],a[N],t[N],maxans;
void Add(int x,int d)
{
for(;x<=n;x+=(x&-x)) t[x]=max(t[x],d);
}
int Fmax(int x)
{
int ans=0;
while(l<=r)
{
if(r-(r&-r)+1<=l) ans=max(ans,t[r]),r-=(r&-r);
else ans=max(ans,a[r]),--r;
}
return ans;
}
for(int i=1;i<=n;++i)
{
f[i]=1+Fmax(i);
Add(i,f[i]);
maxans=max(maxans,f[i]);
}
printf("%d",maxans);
luogu例题
AC code
//P1637
#include
#include
#include
#include
typedef long long ll;
using namespace std;
const int N=3e4+2;
long long n,a[N],ma[N],na,t[N],ans,f[4][N];
void Add(long long x,long long d)
{
for(;x<=na;x+=(x&-x)) t[x]+=d;
}
long long Quest(long long x)
{
long long re=0;
for(;x;x-=(x&-x)) re+=t[x];
return re;
}
void Solve()
{
scanf("%lld",&n);
for(int i=1;i<=n;++i)
scanf("%lld",&a[i]),ma[i]=a[i];
sort(a+1,a+n+1);
na=unique(a+1,a+n+1)-a-1;
for(int i=1;i<=n;++i)
f[1][i]=1,ma[i]=lower_bound(a+1,a+na+1,ma[i])-a;
for(int i=2;i<=3;++i)
{
memset(t,0,sizeof(t));
for(int j=1;j<=n;++j)
{
f[i][j]=Quest(ma[j]-1);
Add(ma[j],f[i-1][j]);
if(i==3) ans+=f[i][j];
}
}
printf("%lld",ans);
}
int main ()
{
Solve();
return 0;
}
优化技巧
建树
每一个节点的值是由所有与自己直接相连的儿子的值求和得到的。即每次确定完儿子的值后，用自己的值更新自己的直接父亲。
这样可把O(nlogn)变为O(n)。
/*O(n)*/
int a[N],t[N];
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
t[i]+=a[i];
if(i+(i&-i)<=n) t[i+(i&-i)]+=t[i]
}
重建
对付多组数据很常见的技巧。如果每次输入新数据时，都memset暴力清空树状数组，就可能会造成超时。因此使用tag标记，存储当前节点上次使用时间（即最近一次是被第几组数据使用）。每次操作时判断这个位置tag中的时间和当前时间是否相同，就可以判断这个位置应该是0还是数组内的值。
/*O(logn)*/
int tag[N],t[N],Tag;
void Add(int x,int d)
{
for(x<=n;x+=(x&-x))
{
if(tag[x]!=Tag) t[x]=0,tag[x]=Tag;
t[x]+=d;
}
}
void Ask(int x)
{
int ans=0;
for(;x;x-=(x&-x))
if(tag[x]==Tag) ans+=t[x];
return ans;
}
++Tag;//重建
lougu例题