数据结构与算法学习笔记:二叉搜索树(下)
- 写在前面:记录学习《恋上数据结构与算法》的过程。
- 课程链接地址:https://ke.qq.com/course/385223
目录
二叉树的遍历(适用于所有二叉树)
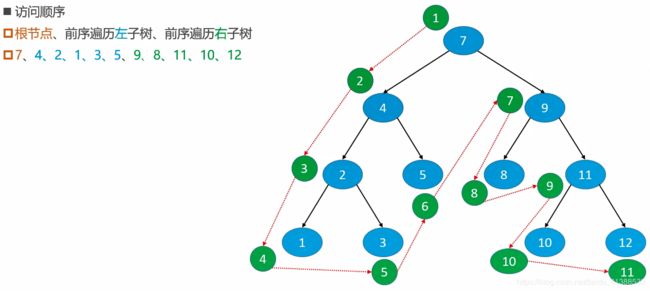
前序遍历
中序遍历
后序遍历
层序遍历
设计遍历接口
增强遍历接口
树状打印二叉树
遍历的应用
计算二叉树的高度
完全二叉树的判断
翻转二叉树
根据遍历结果重构二叉树
前驱节点(predecessor)
后继节点(successor)
删除节点 - 叶子节点
删除节点 - 度为1的节点
删除节点 - 度为2的节点
代码实现
重构代码
简单的继承结构
BinaryTree.java
BST.java
二叉搜索树复杂度分析
二叉树的遍历(适用于所有二叉树)
前序遍历
中序遍历
后序遍历
层序遍历
设计遍历接口
- 前序遍历
增强遍历接口
- 不希望全部遍历完,满足某个条件解终止遍历。
public static abstract class Visitor {
boolean stop;
/**
* @return 如果返回true,就代表停止遍历
*/
public abstract boolean visit(E element);
}
public void preorder(Visitor visitor) {
if (visitor == null) return;
preorder(root, visitor);
}
private void preorder(Node node, Visitor visitor) {
if (node == null || visitor.stop) return;
visitor.stop = visitor.visit(node.element);
preorder(node.left, visitor);
preorder(node.right, visitor);
}
public void inorder(Visitor visitor) {
if (visitor == null) return;
inorder(root, visitor);
}
private void inorder(Node node, Visitor visitor) {
if (node == null || visitor.stop) return;
inorder(node.left, visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
inorder(node.right, visitor);
}
public void postorder(Visitor visitor) {
if (visitor == null) return;
postorder(root, visitor);
}
private void postorder(Node node, Visitor visitor) {
if (node == null || visitor.stop) return;
postorder(node.left, visitor);
postorder(node.right, visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
}
public void levelOrder(Visitor visitor) {
if (root == null || visitor == null) return;
Queue> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
if (visitor.visit(node.element)) return;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
} - 调用
static void test9() {
Integer data[] = new Integer[] {
7, 4, 9, 2, 1
};
BinarySearchTree bst = new BinarySearchTree<>();
for (int i = 0; i < data.length; i++) {
bst.add(data[i]);
}
BinaryTrees.println(bst);
bst.preorder(new Visitor() {
public boolean visit(Integer element) {
System.out.print(element + " ");
return element == 2 ? true : false;
}
});
System.out.println();
bst.inorder(new Visitor() {
public boolean visit(Integer element) {
System.out.print(element + " ");
return element == 4 ? true : false;
}
});
System.out.println();
bst.postorder(new Visitor() {
public boolean visit(Integer element) {
System.out.print(element + " ");
return element == 4 ? true : false;
}
});
System.out.println();
bst.levelOrder(new Visitor() {
public boolean visit(Integer element) {
System.out.print(element + " ");
return element == 9 ? true : false;
}
});
System.out.println();
} 树状打印二叉树
遍历的应用
计算二叉树的高度
- 递归方式
- 利用层序遍历
完全二叉树的判断
- 优化后
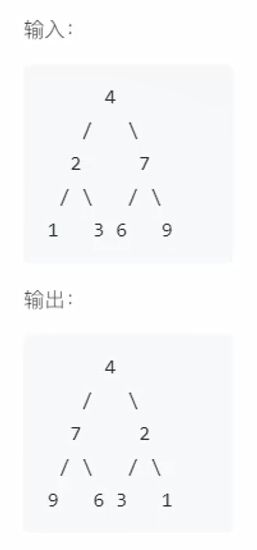
翻转二叉树
- 方法1:前序遍历
- 方法2:后序遍历
- 方法3:中序遍历
- 方法4:层序遍历
根据遍历结果重构二叉树
前驱节点(predecessor)
后继节点(successor)
删除节点 - 叶子节点
删除节点 - 度为1的节点
删除节点 - 度为2的节点
代码实现
- 根据元素查找节点
-
clear
- contains
重构代码
简单的继承结构
BinaryTree.java
package com.mj.tree;
import java.util.LinkedList;
import java.util.Queue;
import com.mj.printer.BinaryTreeInfo;
@SuppressWarnings("unchecked")
public class BinaryTree implements BinaryTreeInfo {
protected int size;
protected Node root;
public int size() {
return size;
}
public boolean isEmpty() {
return size == 0;
}
public void clear() {
root = null;
size = 0;
}
public void preorder(Visitor visitor) {
if (visitor == null) return;
preorder(root, visitor);
}
private void preorder(Node node, Visitor visitor) {
if (node == null || visitor.stop) return;
visitor.stop = visitor.visit(node.element);
preorder(node.left, visitor);
preorder(node.right, visitor);
}
public void inorder(Visitor visitor) {
if (visitor == null) return;
inorder(root, visitor);
}
private void inorder(Node node, Visitor visitor) {
if (node == null || visitor.stop) return;
inorder(node.left, visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
inorder(node.right, visitor);
}
public void postorder(Visitor visitor) {
if (visitor == null) return;
postorder(root, visitor);
}
private void postorder(Node node, Visitor visitor) {
if (node == null || visitor.stop) return;
postorder(node.left, visitor);
postorder(node.right, visitor);
if (visitor.stop) return;
visitor.stop = visitor.visit(node.element);
}
public void levelOrder(Visitor visitor) {
if (root == null || visitor == null) return;
Queue> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
if (visitor.visit(node.element)) return;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
}
public boolean isComplete() {
if (root == null) return false;
Queue> queue = new LinkedList<>();
queue.offer(root);
boolean leaf = false;
while (!queue.isEmpty()) {
Node node = queue.poll();
if (leaf && !node.isLeaf()) return false;
if (node.left != null) {
queue.offer(node.left);
} else if (node.right != null) {
return false;
}
if (node.right != null) {
queue.offer(node.right);
} else { // 后面遍历的节点都必须是叶子节点
leaf = true;
}
}
return true;
}
public int height() {
if (root == null) return 0;
// 树的高度
int height = 0;
// 存储着每一层的元素数量
int levelSize = 1;
Queue> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
Node node = queue.poll();
levelSize--;
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
if (levelSize == 0) { // 意味着即将要访问下一层
levelSize = queue.size();
height++;
}
}
return height;
}
public int height2() {
return height(root);
}
private int height(Node node) {
if (node == null) return 0;
return 1 + Math.max(height(node.left), height(node.right));
}
protected Node predecessor(Node node) {
if (node == null) return null;
// 前驱节点在左子树当中(left.right.right.right....)
Node p = node.left;
if (p != null) {
while (p.right != null) {
p = p.right;
}
return p;
}
// 从父节点、祖父节点中寻找前驱节点
while (node.parent != null && node == node.parent.left) {
node = node.parent;
}
// node.parent == null
// node == node.parent.right
return node.parent;
}
protected Node successor(Node node) {
if (node == null) return null;
// 前驱节点在左子树当中(right.left.left.left....)
Node p = node.right;
if (p != null) {
while (p.left != null) {
p = p.left;
}
return p;
}
// 从父节点、祖父节点中寻找前驱节点
while (node.parent != null && node == node.parent.right) {
node = node.parent;
}
return node.parent;
}
public static abstract class Visitor {
boolean stop;
/**
* @return 如果返回true,就代表停止遍历
*/
abstract boolean visit(E element);
}
protected static class Node {
E element;
Node left;
Node right;
Node parent;
public Node(E element, Node parent) {
this.element = element;
this.parent = parent;
}
public boolean isLeaf() {
return left == null && right == null;
}
public boolean hasTwoChildren() {
return left != null && right != null;
}
}
@Override
public Object root() {
return root;
}
@Override
public Object left(Object node) {
return ((Node)node).left;
}
@Override
public Object right(Object node) {
return ((Node)node).right;
}
@Override
public Object string(Object node) {
Node myNode = (Node)node;
String parentString = "null";
if (myNode.parent != null) {
parentString = myNode.parent.element.toString();
}
return myNode.element + "_p(" + parentString + ")";
}
}
BST.java
package com.mj.tree;
import java.util.Comparator;
@SuppressWarnings("unchecked")
public class BST extends BinaryTree {
private Comparator comparator;
public BST() {
this(null);
}
public BST(Comparator comparator) {
this.comparator = comparator;
}
public void add(E element) {
elementNotNullCheck(element);
// 添加第一个节点
if (root == null) {
root = new Node<>(element, null);
size++;
return;
}
// 添加的不是第一个节点
// 找到父节点
Node parent = root;
Node node = root;
int cmp = 0;
do {
cmp = compare(element, node.element);
parent = node;
if (cmp > 0) {
node = node.right;
} else if (cmp < 0) {
node = node.left;
} else { // 相等
node.element = element;
return;
}
} while (node != null);
// 看看插入到父节点的哪个位置
Node newNode = new Node<>(element, parent);
if (cmp > 0) {
parent.right = newNode;
} else {
parent.left = newNode;
}
size++;
}
public void remove(E element) {
remove(node(element));
}
public boolean contains(E element) {
return node(element) != null;
}
private void remove(Node node) {
if (node == null) return;
size--;
if (node.hasTwoChildren()) { // 度为2的节点
// 找到后继节点
Node s = successor(node);
// 用后继节点的值覆盖度为2的节点的值
node.element = s.element;
// 删除后继节点
node = s;
}
// 删除node节点(node的度必然是1或者0)
Node replacement = node.left != null ? node.left : node.right;
if (replacement != null) { // node是度为1的节点
// 更改parent
replacement.parent = node.parent;
// 更改parent的left、right的指向
if (node.parent == null) { // node是度为1的节点并且是根节点
root = replacement;
} else if (node == node.parent.left) {
node.parent.left = replacement;
} else { // node == node.parent.right
node.parent.right = replacement;
}
} else if (node.parent == null) { // node是叶子节点并且是根节点
root = null;
} else { // node是叶子节点,但不是根节点
if (node == node.parent.left) {
node.parent.left = null;
} else { // node == node.parent.right
node.parent.right = null;
}
}
}
private Node node(E element) {
Node node = root;
while (node != null) {
int cmp = compare(element, node.element);
if (cmp == 0) return node;
if (cmp > 0) {
node = node.right;
} else { // cmp < 0
node = node.left;
}
}
return null;
}
/**
* @return 返回值等于0,代表e1和e2相等;返回值大于0,代表e1大于e2;返回值小于于0,代表e1小于e2
*/
private int compare(E e1, E e2) {
if (comparator != null) {
return comparator.compare(e1, e2);
}
return ((Comparable)e1).compareTo(e2);
}
private void elementNotNullCheck(E element) {
if (element == null) {
throw new IllegalArgumentException("element must not be null");
}
}
}