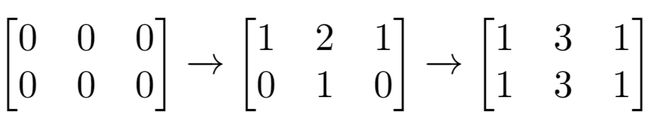leetcode练习题——1
1266. 访问所有点的最小时间*
平面上有 n 个点,点的位置用整数坐标表示 points[i] = [xi, yi]。请你计算访问所有这些点需要的最小时间(以秒为单位)。
你可以按照下面的规则在平面上移动:
每一秒沿水平或者竖直方向移动一个单位长度,或者跨过对角线(可以看作在一秒内向水平和竖直方向各移动一个单位长度)。
必须按照数组中出现的顺序来访问这些点。
![]()
输入:points = [[1,1],[3,4],[-1,0]]
输出:7
解释:一条最佳的访问路径是: [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
从 [1,1] 到 [3,4] 需要 3 秒
从 [3,4] 到 [-1,0] 需要 4 秒
一共需要 7 秒
points.length == n
1 <= n <= 100
points[i].length == 2
-1000 <= points[i][0], points[i][1] <= 1000
判断当前X1,Y1坐标与下一个坐标的X2,Y2差距
1、如果X1,Y1(0,0)都小于X2,Y2(1,1) || X1,Y1(0,0)都大于X2,Y2(-1,-1),斜走?步,直到不满足该条件,?秒时间
2、如果X1小于X2,Y1=Y2 (0,0), (1,0),直走?步,直到不满足该条件,?秒时间
3、如果X1小于X2,Y1>Y2 (0,1), (1,0)斜走?步,直到不满足该条件,?秒时间
4、如果X1大于X2,Y1
5、如果X1大于X2,Y1=Y2 (1,0), (0,0)直走?步,直到不满足该条件,?秒时间
从上可以得知,只要第一个坐标的XY与第二个坐标的XY都不相等,就斜着走 ,只要第一个坐标的XY与第二个坐标的XY有一个相等,就直着走 直到不满足以上条件,就到达目标点
class Solution {
public int minTimeToVisitAllPoints(int[][] points) {
int min = 0;
for (int i = 1; i < points.length; ++i)
min += findMinStep(points[i - 1][0], points[i - 1][1], points[i][0], points[i][1]);
return min;
}
private static int findMinStep(int x1, int y1, int x2, int y2) {
int minSlope = Math.min(Math.abs(x1 - x2), Math.abs(y1 - y2));
return Math.abs(x1 - x2) + Math.abs(y1 - y2) - minSlope;
}
}1351. 统计有序矩阵中的负数
给你一个 m * n 的矩阵 grid,矩阵中的元素无论是按行还是按列,都以非递增顺序排列。
请你统计并返回 grid 中 负数 的数目。
输入:grid = [[4,3,2,-1],[3,2,1,-1],[1,1,-1,-2],[-1,-1,-2,-3]]
输出:8
解释:矩阵中共有 8 个负数。
m == grid.length
n == grid[i].length
1 <= m, n <= 100
-100 <= grid[i][j] <= 100
遍历整个数组即可输出
class Solution {
public int countNegatives(int[][] grid) {
int count=0;
for(int i=0;i1252. 奇数值单元格的数目*
给你一个 n 行 m 列的矩阵,最开始的时候,每个单元格中的值都是 0。另有一个索引数组 indices,indices[i] = [ri, ci] 中的 ri 和 ci 分别表示指定的行和列(从 0 开始编号)。你需要将每对 [ri, ci] 指定的行和列上的所有单元格的值加 1。请你在执行完所有 indices 指定的增量操作后,返回矩阵中 「奇数值单元格」 的数目。
输入:n = 2, m = 3, indices = [[0,1],[1,1]]
输出:6
解释:最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]],里面有 6 个奇数。
1 <= n <= 50
1 <= m <= 50
1 <= indices.length <= 100
0 <= indices[i][0] < n
0 <= indices[i][1] < m
class Solution {
public int oddCells(int n, int m, int[][] indices) {
boolean[] r = new boolean[n];
boolean[] c = new boolean[m];
int i;
for (i = 0; i < indices.length; i++) {
r[indices[i][0]] = !r[indices[i][0]];
c[indices[i][1]] = !c[indices[i][1]];
}
int rr = 0, cc = 0;
for (i = 0; i < r.length; i++) {
if(r[i])rr++;
}
for (i = 0; i < c.length; i++) {
if(c[i])cc++;
}
return rr * m + cc * n - rr * cc * 2;
}
}1304. 和为零的N个唯一整数*
给你一个整数 n,请你返回 任意 一个由 n 个 各不相同 的整数组成的数组,并且这 n 个数相加和为 0 。
输入:n = 5 输出:[-7,-1,1,3,4] 解释:这些数组也是正确的 [-5,-1,1,2,3],[-3,-1,2,-2,4]
1 <= n <= 1000
class Solution {
public int[] sumZero(int n) {
int[] res = new int[n];
int h = 0, t = 0, l = n - 1;
for (int i = 0; i < n / 2; i++) {
res[i] = h + 1;
res[l] = t - 1;
t--;
h++;
l--;
}
return res;
}
}66. 加一
给定一个由整数组成的非空数组所表示的非负整数,在该数的基础上加一。最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。你可以假设除了整数 0 之外,这个整数不会以零开头。
输入: [1,2,3] 输出: [1,2,4] 解释: 输入数组表示数字 123。。。,
import java.util.Arrays;
class Solution66 {
public static void main(String[] args){
int[] digits={9,8,7,6,5,4,3,2,1,0};
System.out.println(Arrays.toString(plusOne(digits)));
}
public static int[] plusOne(int[] digits) {
int carry=1;
for(int i=digits.length-1;i>=0;i--){
int num=digits[i]+carry;
digits[i]=num%10;
carry=num/10;
if(carry==0){
break;
}
}
if(carry==1){ //只能说明数组当中肯定是全9
int[] arr=new int[digits.length+1];
arr[0]=1;
return arr;
}
return digits;
}
}169. 多数元素
给定一个大小为 n 的数组,找到其中的多数元素。多数元素是指在数组中出现次数大于 ⌊ n/2 ⌋ 的元素。你可以假设数组是非空的,并且给定的数组总是存在多数元素
输入: [3,2,3] 输出: 3
class Solution169 {
public int majorityElement(int[] nums) {
//不使用排序 在O(n)解决
int m=nums[0];
int count=1;
for(int i=1;i209. 长度最小的子数组
给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的连续子数组。如果不存在符合条件的连续子数组,返回 0
输入: s = 7, nums = [2,3,1,2,4,3] 输出: 2 解释: 子数组 [4,3] 是该条件下的长度最小的连续子数组。
class Solution209 {
public int minSubArrayLen(int s, int[] nums) {
int len=0;
int i=0;
int sum=0;
for(int j=0;j=s){
len=len==0?(j-i+1):Math.min(len,j-i+1);
sum-=nums[i];
i++;
}
}
return len;
}
} 283. 移动零
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
输入: [0,1,0,3,12] 输出: [1,3,12,0,0]
class Solution {
public void moveZeroes(int[] nums) {
int k=0;
int temp=0;
for(int i=0;i674. 最长连续递增序列
给定一个未经排序的整数数组,找到最长且连续的的递增序列。
输入: [1,3,5,4,7]
输出: 3
解释: 最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的,因为5和7在原数组里被4隔开。
class Solution674 {
public static void main(String[] args){
int[] nums={2,2,2,2};
int len=findLengthOfLCIS(nums);
System.out.println(len);
}
public static int findLengthOfLCIS(int[] nums) {
if(nums.length==0||nums.length==1){
return nums.length;
}
int maxL=0;
int maxR=0;
int l=0;
int r=0;
int maxCount=1;
int count=1;
for(int i=0;inums[i]){
count++;
r=i+1;
}else{
count=1;
l=i+1;
r=i+1;
}
if(count>maxCount){
maxCount=count;
maxL=l;
maxR=r;
}
}
System.out.println(maxL+"~"+maxR);
return maxCount;
}
} 724. 寻找数组的中心索引
给定一个整数类型的数组 nums,请编写一个能够返回数组“中心索引”的方法。我们是这样定义数组中心索引的:数组中心索引的左侧所有元素相加的和等于右侧所有元素相加的和。如果数组不存在中心索引,那么我们应该返回 -1。如果数组有多个中心索引,那么我们应该返回最靠近左边的那一个。
输入:
nums = [1, 7, 3, 6, 5, 6]
输出: 3
解释:
索引3 (nums[3] = 6) 的左侧数之和(1 + 7 + 3 = 11),与右侧数之和(5 + 6 = 11)相等。
同时, 3 也是第一个符合要求的中心索引。
class Solution724 {
public int pivotIndex(int[] nums) {
int sum=0;
for(int num:nums){
sum+=num;
}
int leftSum=0;
int rightSum=0;
for(int i=0;i905. 按奇偶排序数组
给定一个非负整数数组 A,返回一个数组,在该数组中, A 的所有偶数元素之后跟着所有奇数元素。你可以返回满足此条件的任何数组作为答案。
输入:[3,1,2,4] 输出:[2,4,3,1] 输出 [4,2,3,1],[2,4,1,3] 和 [4,2,1,3] 也会被接受。
1 <= A.length <= 50000 <= A[i] <= 5000
class Solution905 {
public int[] sortArrayByParity(int[] A) {
int left=0;
int right=A.length-1;
while(left1013. 将数组分成和相等的三个部分
给定一个整数数组 A,只有我们可以将其划分为三个和相等的非空部分时才返回 true,否则返回 false。
形式上,如果我们可以找出索引 i+1 < j 且满足 (A[0] + A[1] + ... + A[i] == A[i+1] + A[i+2] + ... + A[j-1] == A[j] + A[j-1] + ... + A[A.length - 1]) 就可以将数组三等分
输出:[0,2,1,-6,6,-7,9,1,2,0,1]
输出:true
解释:0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
3 <= A.length <= 50000-10000 <= A[i] <= 10000
class Solution1013 {
public boolean canThreePartsEqualSum(int[] A) {
int sum=0;
for(int num:A){
sum+=num;
}
int key=sum/3;
int group=0;
for(int i=0;i来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/find-pivot-index