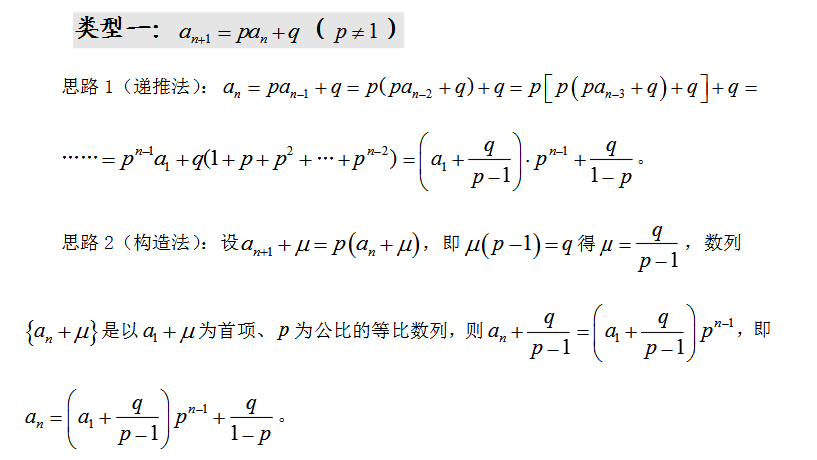小知识点汇总(实时更新)
17/2/11
1.已知三角形三个顶点坐标，则边长，周长，面积，重心，外心公式：
//设三个顶点坐标为（x1,y1）（x2,y2）（x3,y3）double a=sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));//边长
double b=sqrt((x1-x3)*(x1-x3)+(y1-y3)*(y1-y3));
double c=sqrt((x3-x2)*(x3-x2)+(y3-y2)*(y3-y2));double zhouchang(double a,double b,double c)
{
return a+b+c;
}
double mianji(double a,double b,double c)
{
double t=(a+b+c)/2;
return sqrt(t*(t-a)*(t-b)*(t-c));
}A1=2*(x2-x1);
B1=2*(y2-y1);
C1=x2*x2+y2*y2-x1*x1-y1*y1;
A2=2*(x3-x2);
B2=2*(y3-y2);
C2=x3*x3+y3*y3-x2*x2-y2*y2;
x=((C1*B2)-(C2*B1))/((A1*B2)-(A2*B1));
y=((A1*C2)-(A2*C1))/((A1*B2)-(A2*B1));
printf("%.2lf %.2lf\n",x,y);//外心
x0=(x1+x2+x3)/3;
y0=(y1+y2+y3)/3;
printf("%.2lf %.2lf\n",x0,y0);//重心 17/2/12
2.关于DP的四边形不等式优化方法及证明：
转载于：http://www.cnblogs.com/jiu0821/p/4493497.html
四边形不等式优化动态规划原理:
1.当决策代价函数w[i][j]满足w[i][j]+w[i’][j’]<=w[I'][j]+w[i][j’](i<=i’<=j<=j’)时,称w满足四边形不等式.当函数w[i][j]满足w[i’][j]<=w[i][j’] i<=i’<=j<=j’)时,称w关于区间包含关系单调.
2.如果状态转移方程m为
且决策代价w满足四边形不等式的单调函数(可以推导出m亦为满足四边形不等式的单调函数),则可利用四边形不等式推出最优决策s的单调函数性,从而减少每个状态的状态数,将算法的时间复杂度由原来的O(n^3)降低为O(n^2).方法是通过记录子区间的最优决策来减少当前的决策量.令:
s[i][j]=max{k | ma[i][j] = m[i][k-1] + m[k][j] + w[i][j]}
由于决策s具有单调性,因此状态转移方程可修改为:
证明过程: (转载)
设m[i,j]表示动态规划的状态量。
m[i,j]有类似如下的状态转移方程：
m[i,j]=opt{m[i,k]+m[k,j]}(i≤k≤j)
如果对于任意的a≤b≤c≤d，有m[a,c]+m[b,d]≤m[a,d]+m[b,c]，那么m[i,j]满足四边形不等式。
以上是适用这种优化方法的必要条件
对于一道具体的题目，我们首先要证明它满足这个条件，一般来说用数学归纳法证明，根据题目的不同而不同。
通常的动态规划的复杂度是O(n3)，我们可以优化到O(n2)
设s[i,j]为m[i,j]的决策量，即m[i,j]=m[i,s[i,j]]+m[s[i,j]+j]
我们可以证明，s[i,j-1]≤s[i,j]≤s[i+1,j] （证明过程见下）
那么改变状态转移方程为：
m[i,j]=opt{m[i,k]+m[k,j]} (s[i,j-1]≤k≤s[i+1,j])
复杂度分析：不难看出，复杂度决定于s的值，以求m[i,i+L]为例，
(s[2,L+1]-s[1,L])+(s[3,L+2]-s[2,L+1])…+(s[n-L+1,n]-s[n-L,n-1])=s[n-L+1,n]-s[1,L]≤n
所以总复杂度是O(n2)
对s[i,j-1]≤s[i,j]≤s[i+1,j]的证明：
设mk[i,j]=m[i,k]+m[k,j]，s[i,j]=d
对于任意k
(mk[i+1,j]-md[i+1,j]) - (mk[i,j]-md[i,j])
=(mk[i+1,j]+md[i,j]) - (md[i+1,j]+mk[i,j])
=(m[i+1,k]+m[k,j]+m[i,d]+m[d,j]) - (m[i+1,d]+m[d,j]+m[i,k]+m[k,j])
=(m[i+1,k]+m[i,d]) - (m[i+1,d]+m[i,k])
∵m满足四边形不等式，∴对于i
∴(mk[i+1,j]-md[i+1,j])≥(mk[i,j]-md[i,j])≥0
∴s[i,j]≤s[i+1,j]，同理可证s[i,j-1]≤s[i,j]
证毕
扩展：
以上所给出的状态转移方程只是一种比较一般的，其实，很多状态转移方程都满足四边形不等式优化的条件。
解决这类问题的大概步骤是：
0.证明w满足四边形不等式，这里w是m的附属量，形如m[i,j]=opt{m[i,k]+m[k,j]+w[i,j]}，此时大多要先证明w满足条件才能进一步证明m满足条件
1.证明m满足四边形不等式
2.证明s[i,j-1]≤s[i,j]≤s[i+1,j]
3.单调队列优化DP
空间有限就不复制了，直接上链接吧：http://www.cnblogs.com/ka200812/archive/2012/07/11/2585950.html
个人感觉他的单调队列的介绍部分有点瑕疵，仁者见仁智者见智吧，不过下面给的两个例子和讲解还是很好的。用来学单调队列优化DP很不错。
关于单调队列优化多重背包的证明请戳这里和这里，虽然网上证明很多，但是感觉都不是那种特别清楚明了的，还是要多看看然后自己总结总结。模板戳这里。
17/2/22
4.数据输入输出
scanf（“%s %s”，...）；可以完美解决输入两个用空格隔开的字符串的情况。（注意两个%s中间有空格）同理，也可以解决其他类似的输入，例如 要输入“（1,1）”（不含引号）则可以写成scanf（“（%d，%d）”，....）；
%o八进制输入输出
%x十六进制输入输出（字母小写）
%X十六进制输入输出（字母大写）
%e科学计数法输入输出，注意变量类型要使用float
%g 根据浮点数精度选择用%f还是%e输出，输入时同%f差不多，输出支持六位精度，同时会自动去除无用的0.
17/4/11更新：
昨天又在某学长那里学到骚东西，%1d 可以支持每次只读入一个数字，这样当读入连续数字间没有空格时就不用再自己写个转化函数了。以此类推，还有%2d %3d……
17/5/23更新：
昨天又受到了学长的调教，scanf("%*s %s",str); 可以跳过第一个字符串直接从输入流读取同一行中第二个字符串到str中。
printf("%*s",len,str);可以把str固定为长度len输出(右对齐,strlen(str)>len的话输出长度为strlen(str))printf("%-*s",len,str);（左对齐）
printf("%*.*lf",len,x,1.23456);可以把浮点数固定格式为总长度为len，浮点部分长度为x（不够补零，多出四舍五入）（右对齐）
printf("%-*.*lf",len,x,1.23456);（左对齐）
17/2/24
5.spfa的优化：
SPFA 是按照 FIFO 的原则更新距离的, 没有考虑到距离标号的作用。
实现中 SPFA 有两个非常著名的优化: SLF 和 LLL。
SLF: Small Label First 策略. （比较常用）
实现方法：设队首元素为 a, 队列中要加入节点 b, 在b<=a时加到队首而不是队尾, 否则和普通的 SPFA 一样加到队尾.
LLL: Large Label Last 策略. （不太常用）
设队列 Q 中的队首元素为 i，距离标号的平均值为 
，每次出队时，若 
，把 i 移到队列末尾，如此反复，直到找到一个 
使 
，将其出队。（以上转自http://www.cnblogs.com/pony1993/archive/2012/09/07/2675654.html）
核心代码：
if(!book[v])
{
if(!q.empty()&&dis[v]>dis[q.front()])
q.push_back(v);
else
q.push_front(v);
book[v]=true;
}//注意这里的q是dequeq; 17/3/12
6.10进制整数转任意负进制：
比如10进制要转-R进制，同样也是不断取模(-R)，整除(-R)，那么问题就是有的位上会出现负数，这不符合-R进制的数字局限
有个很巧妙的方法，就是给这个位置上的数+R，那么整个数字就改变了R*R^i=R^(i+1)，那么第i+1位上的数字加上一个1即可（因为相邻位正负性恰好相反）
具体做的时候，不断取模-R，如果发现某位<0，给这位+R，给剩余整除的数+1即可
17/3/24
杂记：
将一个数素因子拆分，例如18=2^1*3^2,则36的因子个数有(1+1)*(2+1)=6个，即将x素因子拆分后的所有素因子的幂次加一再相乘就等于x的因子个数，可以用来快速求一个数的因子个数。
输入输出：
用cin和cout的时候可以在主函数最前面加上std::ios::sync_with_stdio(0);这句话可以加速输入输出，速度与scanf几乎无异。
但是！不知是OJ的原因还是编译器原因，某些题加上这句话就会TLE。。亲身体会，同样的代码，加上TLE，不加19ms。。因此慎用。
3/27注：经过大神提示+百度，发现TLE原因不是OJ原因也不是编译器问题。。而是我自己不知道原理就XJB用，正确用法是在加上这句话以后就不能将stdin和stdout与cin和cout混用了，即不能再使用scanf和printf，至于原因，涉及到了输入输出流同步的问题，在此贴出链接自行查阅：
http://www.cnblogs.com/PrayG/p/5749832.html
5/24注：当输入数据量特别大的时候（1e5、1e6）加速也显得很无力了，和scanf速度能相差好几倍，还是乖乖的用scanf吧。。毕竟因为这个T了可能会哭的。
freopen函数：
将输入输出流重定向，一般用于写入或读出文件，如果要在文件输入输出和标准输入输出中来回切换多次不建议使用。
示例代码：
freopen("in.txt","r",stdin);
freopen("out.txt","w",stdout);
fclose(stdin);
fclose(stdout);
17/5/11
上段时间忙着准备省赛，好长时间没更新了。。
STL 的一些骚东西：
__gcd(x,y)可以直接求两个数的gcd，注意前面是两个下划线。
atoi（string.c_str()）可以直接将字符串转化成整形，同时自动去除前导零。同理atof（string.c_str()）直接转化成浮点型。
transform（s.begin(),s.end(),toupper）可以直接将所有字母转化成大写，upper换成lower可以转化成小写。
STL还有许许多多骚东西。。一时也学不完，啥时候学了就来更新更新。
17/6/6
数学小知识：
这个可以在有除法且分母和模数不互质时用到。
这个可以在求线性序列的通项时用到（可这TM不是高中时的水题吗。。。现在竟然沦落到要写博客才能记住了。。）
17/7/9
最近get的新技能：欧拉筛，能求素数也能用来求最小质因数还用许多高级应用（待学）。复杂度O(n)。
int fac[MAXN],p[MAXN];//fac里面存的是最小质因子，p里面存的是素数
void init()
{
int cnt=0;
for(int i=2;i17/7/22
又新学到了库函数的骚东西，众所周知sort是默认按从小到大排序的，原来我要从大到小排序的时候都是要重载自定义函数cmp，其实不用那么麻烦的，sort（begin，end，greater
lower_bound(begin, end, num, greater
17/7/26
又㕛叒叕学到了STL骚东西：
nth_element()库函数
基本格式：
nth_element(arr.begin(), arr + n - 1, arr.end)
调用函数后保证比第n个数小的数都在前面，比它大的数在后面
此函数以平均O(n)的时间复杂度求出区间中的第n小的数，同sort一样，函数最后也能加上重载的cmp函数。