Kuangbin专题八生成树

这个专题真是做的人欲生欲死，模型太多了，我就当板子用吧。。。

A - The Unique MST

 POJ - 1679

Given a connected undirected graph, tell if its minimum spanning tree is unique. 

Definition 1 (Spanning Tree): Consider a connected, undirected graph G = (V, E). A spanning tree of G is a subgraph of G, say T = (V', E'), with the following properties: 
1. V' = V. 
2. T is connected and acyclic. 

Definition 2 (Minimum Spanning Tree): Consider an edge-weighted, connected, undirected graph G = (V, E). The minimum spanning tree T = (V, E') of G is the spanning tree that has the smallest total cost. The total cost of T means the sum of the weights on all the edges in E'. 

Input

The first line contains a single integer t (1 <= t <= 20), the number of test cases. Each case represents a graph. It begins with a line containing two integers n and m (1 <= n <= 100), the number of nodes and edges. Each of the following m lines contains a triple (xi, yi, wi), indicating that xi and yi are connected by an edge with weight = wi. For any two nodes, there is at most one edge connecting them.

Output

For each input, if the MST is unique, print the total cost of it, or otherwise print the string 'Not Unique!'.

Sample Input

2
3 3
1 2 1
2 3 2
3 1 3
4 4
1 2 2
2 3 2
3 4 2
4 1 2

Sample Output

3
Not Unique!

题目让判断最小生成树是否唯一，解法是看次小生成树是否等于最小生成树。

求次小生成树可以直接套板子，，，做法是在贪心的Prim基础上动态规划出在MST上点i到点j的最长边。

核心代码是

 if(used[j] && j != p)
     maxe[j][p] = maxe[p][j] = max(maxe[j][pre[p]], lowc[p]);

第一点是j!=p这题数据没这个能过，但是后面的题目没这个过不了，因为改变maxe[p][p]后就相当于多了一个值为max(maxe[j][pre[p]], lowc[p])的自环，以后包含p点的路可能会受到影响。

然后动规方程意思是点j和p之间的最大边是j到pre[p]的最大边和p到pre[p]这条边最大的一个。

最后求次小生成树就是在最小生成树中加一条边e形成环，然后在该环中减去原树最大的的一条边(maxe[i][j])。

#include 
#include 
#include 
#include 
#include 

B - Qin Shi Huang's National Road System

 HDU - 4081

During the Warring States Period of ancient China(476 BC to 221 BC), there were seven kingdoms in China ---- they were Qi, Chu, Yan, Han, Zhao, Wei and Qin. Ying Zheng was the king of the kingdom Qin. Through 9 years of wars, he finally conquered all six other kingdoms and became the first emperor of a unified China in 221 BC. That was the Qin dynasty ---- the first imperial dynasty of China(not to be confused with the Qing Dynasty, the last dynasty of China). So Ying Zheng named himself "Qin Shi Huang" because "Shi Huang" means "the first emperor" in Chinese. 

Qin Shi Huang undertook gigantic projects, including the first version of the Great Wall of China, the now famous city-sized mausoleum guarded by a life-sized Terracotta Army, and a massive national road system. There is a story about the road system: 
There were n cities in China and Qin Shi Huang wanted them all to be connected by n-1 roads, in order that he could go to every city from the capital city Xianyang. 
Although Qin Shi Huang was a tyrant, he wanted the total length of all roads to be minimum,so that the road system may not cost too many people's life. A daoshi (some kind of monk) named Xu Fu told Qin Shi Huang that he could build a road by magic and that magic road would cost no money and no labor. But Xu Fu could only build ONE magic road for Qin Shi Huang. So Qin Shi Huang had to decide where to build the magic road. Qin Shi Huang wanted the total length of all none magic roads to be as small as possible, but Xu Fu wanted the magic road to benefit as many people as possible ---- So Qin Shi Huang decided that the value of A/B (the ratio of A to B) must be the maximum, which A is the total population of the two cites connected by the magic road, and B is the total length of none magic roads. 
Would you help Qin Shi Huang? 
A city can be considered as a point, and a road can be considered as a line segment connecting two points.

Input

The first line contains an integer t meaning that there are t test cases(t <= 10). 
For each test case: 
The first line is an integer n meaning that there are n cities(2 < n <= 1000). 
Then n lines follow. Each line contains three integers X, Y and P ( 0 <= X, Y <= 1000, 0 < P < 100000). (X, Y) is the coordinate of a city and P is the population of that city. 
It is guaranteed that each city has a distinct location.

Output

For each test case, print a line indicating the above mentioned maximum ratio A/B. The result should be rounded to 2 digits after decimal point.

Sample Input

2
4
1 1 20
1 2 30
200 2 80
200 1 100
3
1 1 20
1 2 30
2 2 40

Sample Output

65.00
70.00

A / B最大，不难想A一定是生成树的一条边，且这棵树不是最小生成树就是次小生成树。

#include 
#include 
#include 
#include 
#include 

C - ACM Contest and Blackout

 UVA - 10600

In order to prepare the “The First National ACM School Contest” (in 20??) the major of the city decided to provide all the schools with a reliable source of power. (The major is really afraid of blackoutsJ). So, in order to do that, power station “Future” and one school (doesn’t matter which one) must be connected; in addition, some schools must be connected as well. You may assume that a school has a reliable source of power if it’s connected directly to “Future”, or to any other school that has a reliable source of power. You are given the cost of connection between some schools. The major has decided to pick out two the cheapest connection plans – the cost of the connection is equal to the sum of the connections between the schools. Your task is to help the major — find the cost of the two cheapest connection plans. Input The Input starts with the number of test cases, T (1 < T < 15) on a line. Then T test cases follow. The first line of every test case contains two numbers, which are separated by a space, N (3 < N < 100) the number of schools in the city, and M the number of possible connections among them. Next M lines contain three numbers Ai , Bi , Ci , where Ci is the cost of the connection (1 < Ci < 300) between schools Ai and Bi . The schools are numbered with integers in the range 1 to N. Output For every test case print only one line of output. This line should contain two numbers separated by a single space – the cost of two the cheapest connection plans. Let S1 be the cheapest cost and S2 the next cheapest cost. It’s important, that S1 = S2 if and only if there are two cheapest plans, otherwise S1 < S2. You can assume that it is always possible to find the costs S1 and S2.

Sample Input

2 5 8 1 3 75 3 4 51 2 4 19 3 2 95 2 5 42 5 4 31 1 2 9 3 5 66 9 14 1 2 4 1 8 8 2 8 11 3 2 8 8 9 7 8 7 1 7 9 6 9 3 2 3 4 7 3 6 4 7 6 2 4 6 14 4 5 9 5 6 10

Sample Output

110 121 37 37

找最小和次小生成树。

#include 
#include 
#include 
#include 
#include 

D - Is There A Second Way Left?

 UVA - 10462

Nasa, being the most talented programmer of his time, can’t think things to be so simple. Recently all his neighbors have decided to connect themselves over a network (actually all of them want to share a broadband internet connection :-)). But he wants to minimize the total cost of cable required as he is a bit fastidious about the expenditure of the project. For some unknown reasons, he also wants a second way left. I mean, he wants to know the second best cost (if there is any which may be same as the best cost) for the project. I am sure, he is capable of solving the problem. But he is very busy with his private affairs(?) and he will remain so. So, it is your turn to prove yourself a good programmer. Take the challenge (if you are brave enough)...

Input

Input starts with an integer t ≤ 1000 which denotes the number of test cases to handle. Then follows t datasets where every dataset starts with a pair of integers v (1 ≤ v ≤ 100) and e (0 ≤ e ≤ 200). v denotes the number of neighbors and e denotes the number of allowed direct connections among them. The following e lines contain the description of the allowed direct connections where each line is of the form ‘start end cost’, where start and end are the two ends of the connection and cost is the cost for the connection. All connections are bi-directional and there may be multiple connections between two ends.

Output

There may be three cases in the output 1. No way to complete the task, 2. There is only one way to complete the task, 3. There are more than one way. Output ‘No way’ for the first case, ‘No second way’ for the second case and an integer c for the third case where c is the second best cost. Output for a case should start in a new line.

Sample Input

4 5 4 1 2 5 3 2 5 4 2 5 5 4 5 5 3 1 2 5 3 2 5 5 4 5 5 5 1 2 5 3 2 5 4 2 5 5 4 5 4 5 6 1 0

Sample Output

Case #1 : No second way

Case #2 : No way

Case #3 : 21

Case #4 : No second way

次小生成树。

#include 
#include 
#include 
#include 
#include 

E - Command Network

 POJ - 3164

After a long lasting war on words, a war on arms finally breaks out between littleken’s and KnuthOcean’s kingdoms. A sudden and violent assault by KnuthOcean’s force has rendered a total failure of littleken’s command network. A provisional network must be built immediately. littleken orders snoopy to take charge of the project.

With the situation studied to every detail, snoopy believes that the most urgent point is to enable littenken’s commands to reach every disconnected node in the destroyed network and decides on a plan to build a unidirectional communication network. The nodes are distributed on a plane. If littleken’s commands are to be able to be delivered directly from a node A to another node B, a wire will have to be built along the straight line segment connecting the two nodes. Since it’s in wartime, not between all pairs of nodes can wires be built. snoopy wants the plan to require the shortest total length of wires so that the construction can be done very soon.

Input

The input contains several test cases. Each test case starts with a line containing two integer N (N ≤ 100), the number of nodes in the destroyed network, and M (M ≤ 104), the number of pairs of nodes between which a wire can be built. The next Nlines each contain an ordered pair xi and yi, giving the Cartesian coordinates of the nodes. Then follow M lines each containing two integers i and j between 1 and N(inclusive) meaning a wire can be built between node i and node j for unidirectional command delivery from the former to the latter. littleken’s headquarter is always located at node 1. Process to end of file.

Output

For each test case, output exactly one line containing the shortest total length of wires to two digits past the decimal point. In the cases that such a network does not exist, just output ‘poor snoopy’.

Sample Input

4 6
0 6
4 6
0 0
7 20
1 2
1 3
2 3
3 4
3 1
3 2
4 3
0 0
1 0
0 1
1 2
1 3
4 1
2 3

Sample Output

31.19
poor snoopy

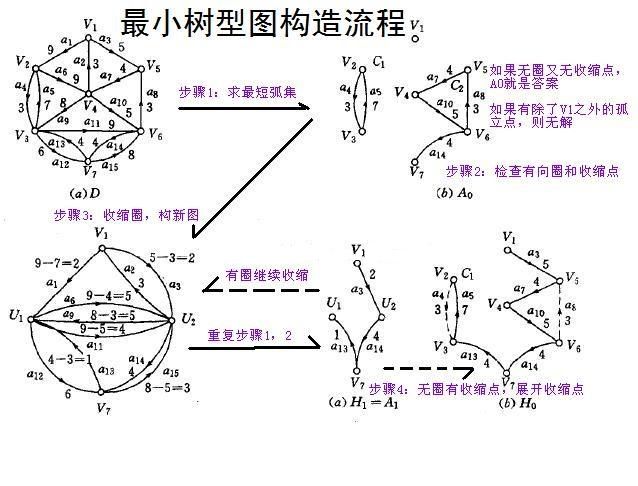
最小树形图，朱刘算法。

昂有向图嘛就不能直接贪心选最小边emmmmmm但还是贪心的算法。

这个著名图片（百度的博客都有它）显示了算法流程：先求出最短弧的集合，然后最短弧组成的图上检查是否有圈，有圈就缩点，再检查有没有圈有就再缩直到无圈再展开收缩点，展开的就是最小属性图。

1.求出最短弧的集合。求出来后要是有点（除了root）没入边肯定凉直接return。

2.求出最短弧集我们可以认为最短弧集里的弧组成的图的圈去掉入v1的边的径一定是最终最小树形图的一部分，我们将这个圈缩点（原图中入收缩点的边要减去圈中入原图中入收缩点的边入的圈中的点的边的值，）不考虑，从剩下的图中继续这样操作。

3.因为一般只需要求值，所以不需要真的展开缩点，只需要在缩点的时候记录值就行了。

#include 
#include 
#include 
#include 
#include 

F - Teen Girl Squad

 UVA - 11183 

You are part of a group of n teenage girls armed with cellphones. You have some news you want to tell everyone in the group. The problem is that no two of you are in the same room, and you must communicate using only cellphones. What’s worse is that due to excessive usage, your parents have refused to pay your cellphone bills, so you must distribute the news by calling each other in the cheapest possible way. You will call several of your friends, they will call some of their friends, and so on until everyone in the group hears the news. Each of you is using a different phone service provider, and you know the price of girl A calling girl B for all possible A and B. Not all of your friends like each other, and some of them will never call people they don’t like. Your job is to find the cheapest possible sequence of calls so that the news spreads from you to all n-1 other members of the group. Input The first line of input gives the number of cases, N (N < 150). N test cases follow. Each one starts with two lines containing n (0 ≤ n ≤ 1000) and m (0 ≤ m ≤ 40, 000). Girls are numbered from 0 to n-1, and you are girl 0. The next m lines will each contain 3 integers, u, v and w, meaning that a call from girl u to girl v costs w cents (0 ≤ w ≤ 1000). No other calls are possible because of grudges, rivalries and because they are, like, lame. The input file size is around 1200 KB. Output For each test case, output one line containing ‘Case #x:’ followed by the cost of the cheapest method of distributing the news. If there is no solution, print ‘Possums!’ instead. Sample Input 4 2 1 0 1 10 2 1 1 0 10 4 4 0 1 10 0 2 10 1 3 20 2 3 30 4 4 0 1 10 1 2 20 2 0 30 2 3 100 Sample Output Case #1: 10 Case #2: Possums! Case #3: 40 Case #4: 130

最小树形图板子题。

#include 
#include 
#include 
#include 
#include 

G - Ice_cream’s world II

 HDU - 2121

After awarded lands to ACMers, the queen want to choose a city be her capital. This is an important event in ice_cream world, and it also a very difficult problem, because the world have N cities and M roads, every road was directed. Wiskey is a chief engineer in ice_cream world. The queen asked Wiskey must find a suitable location to establish the capital, beautify the roads which let capital can visit each city and the project’s cost as less as better. If Wiskey can’t fulfill the queen’s require, he will be punishing.

Input

Every case have two integers N and M (N<=1000, M<=10000), the cities numbered 0…N-1, following M lines, each line contain three integers S, T and C, meaning from S to T have a road will cost C.

Output

If no location satisfy the queen’s require, you must be output “impossible”, otherwise, print the minimum cost in this project and suitable city’s number. May be exist many suitable cities, choose the minimum number city. After every case print one blank. 

Sample Input

3 1
0 1 1

4 4
0 1 10
0 2 10
1 3 20
2 3 30

Sample Output

impossible

40 0

这题是不定根的最小树形图，解法是加一个炒鸡源点，让这个源点连着所有点，赋值为大数，最后结果如果小于两倍的大数就说明ok。这个根的查找我不怎么懂，为什么根要不停更新呢？难道不是找到的第一个pos的边就是结果吗？

对此网上的博客没有找到说清楚的，有个人是这么说的“在无环也就是不需要更新图的时候这样的确是对的，但是一旦图被更新，这样一来点和点之间的对应关系就错了。”点和点之间的对应关系大概就是边了，大概是缩点的时候会改变边？连着被缩的点的边可能会影响pos指向的边？？？观察了几组数据是这样的。注释瞎写了一波。

数据：

3 3
0 1 1
1 2 4
2 0 1

7 15
0 1 9
0 4 5
3 0 3
1 3 9
4 3 4
2 1 7
1 2 3
2 3 8
3 5 5
5 4 3
2 5 9
6 2 4
2 6 6
6 5 4
5 6 8

这两个数据都是缩点后改变pos的。

#include 
#include 
#include 
#include 
#include 

H - Transfer water

 HDU - 4009

XiaoA lives in a village. Last year flood rained the village. So they decide to move the whole village to the mountain nearby this year. There is no spring in the mountain, so each household could only dig a well or build a water line from other household. If the household decide to dig a well, the money for the well is the height of their house multiplies X dollar per meter. If the household decide to build a water line from other household, and if the height of which supply water is not lower than the one which get water, the money of one water line is the Manhattan distance of the two households multiplies Y dollar per meter. Or if the height of which supply water is lower than the one which get water, a water pump is needed except the water line. Z dollar should be paid for one water pump. In addition,therelation of the households must be considered. Some households may do not allow some other households build a water line from there house. Now given the 3‐dimensional position (a, b, c) of every household the c of which means height, can you calculate the minimal money the whole village need so that every household has water, or tell the leader if it can’t be done.

Input

Multiple cases. 
First line of each case contains 4 integers n (1<=n<=1000), the number of the households, X (1<=X<=1000), Y (1<=Y<=1000), Z (1<=Z<=1000). 
Each of the next n lines contains 3 integers a, b, c means the position of the i‐th households, none of them will exceeded 1000. 
Then next n lines describe the relation between the households. The n+i+1‐th line describes the relation of the i‐th household. The line will begin with an integer k, and the next k integers are the household numbers that can build a water line from the i‐th household. 
If n=X=Y=Z=0, the input ends, and no output for that. 

Output

One integer in one line for each case, the minimal money the whole village need so that every household has water. If the plan does not exist, print “poor XiaoA” in one line. 

Sample Input

2 10 20 30
1 3 2
2 4 1
1 2
2 1 2
0 0 0 0

Sample Output

30

和上一题一样，只是建图不一样，也是要找根。

#include 
#include 
#include 
#include 
#include 

I - Organising the Organisation

 UVA - 10766

I am the chief of the Personnel Division of a moderate-sized company that wishes to remain anonymous, and I am currently facing a small problem for which I need a skilled programmer’s help. Currently, our company is divided into several more or less independent divisions. In order to make our business more efficient, these need to be organised in a hierarchy, indicating which divisions are in charge of other divisions. For instance, if there are four divisions A, B, C and D we could organise them as in Figure 1, with division A controlling divisions B and D, and division D controlling division C. One of the divisions is Central Management (division A in the figure above), and should of course be at the top of the hierarchy, but the relative importance of the remaining divisions is not determined, so in Figure 1 above, division C and D could equally well have switched places so that C was in charge over division D. One complication, however, is that it may be impossible to get some divisions to cooperate with each other, and in such a case, neither of these divisions can be directly in charge of the other. For instance, if in the example above A and D are unable to cooperate, Figure 1 is not a valid way to organise the company. In general, there can of course be many different ways to organise the organisation, and thus it is desirable to find the best one (for instance, it is not a good idea to let the programming people be in charge of the marketing people). This job, however, is way too complicated for you, and your job is simply to help us find out how much to pay the consultant that we hire to find the best organisation for us. In order to determine the consultant’s pay, we need to find out exactly how difficult the task is, which is why you have to count exactly how many different ways there are to organise the organisation. Oh, and I need the answer in five hours. Input The input consists of a series of test cases, at most 50, terminated by end-of-file. Each test cases begins with three integers n, m, k (1 ≤ n ≤ 50, 1 ≤ m ≤ n, 0 ≤ k ≤ 1500). n denotes the number of divisions in the company (for convenience, the divisions are numbered from 1 to n), and k indicates which division is the Central Management division. This is followed by m lines, each containing two integers 1 ≤ i, j ≤ n, indicating that division i and division j cannot cooperate (thus, i cannot be directly in charge of j and j cannot be directly in charge of i). You may assume that i and j are always different. Output For each test case, print the number of possible ways to organise the company on a line by itself. This number will be at least 1 and at most 1015 . Note: The three possible hierarchies in the first sample case Sample Input 5 5 2 3 1 3 4 4 5 1 4 5 3 4 1 1 1 4 3 0 2 Sample Output 3 8 3

生成树计数。矩阵树定理。矩阵树定理的证明里面有很多线性代数知识，我想专门写一篇博客。

百度的题解都是浮点数的，，，我一开始也就抄了个浮点数的，然后发现可以直接long long。

//#include 
//#include 
//#include 
//#include 
//#include 

J - Find The Determinant III

 SPOJ - DETER3

Given a NxN matrix A, find the Determinant of A % P.

Input

Multiple test cases (the size of input file is about 3MB, all numbers in each matrix are generated randomly).

The first line of every test case contains two integers , representing N (0 < N < 201) and P (0 < P < 1,000,000,001). The following N lines each contain N integers, the j-th number in i-th line represents A[i][j] (- 1,000,000,001 < A[i][j] < 1,000,000,001).

Output

For each test case, print a single line contains the answer.

Example

Input:
1 10
-528261590
2 2
595698392 -398355861
603279964 -232703411
3 4
-840419217 -895520213 -303215897
537496093 181887787 -957451145
-305184545 584351123 -257712188

Output:
0
0
2

裸的求行列式，套板子就好啦！

#include 
#include 
#include 
#include 
#include 

K - Join

 URAL - 1627

Businessman Petya recently bought a new house. This house has one floor with n × msquare rooms, placed in rectangular lattice. Some rooms are pantries and the other ones are bedrooms. Now he wants to join all bedrooms with doors in such a way that there will be exactly one way between any pair of them. He can make doors only between neighbouring bedrooms (i.e. bedrooms having a common wall). Now he wants to count the number of different ways he can do it.

Input

First line contains two integers n and m (1 ≤ n, m ≤ 9)  — the number of lines and columns in the lattice. Next n lines contain exactly m characters representing house map, where "." means bedroom and "*" means pantry. It is guaranteed that there is at least one bedroom in the house.

Output

Output the number of ways to join bedrooms modulo 10 9.

Example

input	output
2 2 .. ..	4
2 2 *. .*	0

 

有了板子就难在建图，其实给每个房间编号就行，能做其实、、、

#include 
#include 
#include 
#include 
#include 

L - Lightning

 HDU - 4305

There are N robots standing on the ground (Don't know why. Don't know how). 

Suddenly the sky turns into gray, and lightning storm comes! Unfortunately, one of the robots is stuck by the lightning! 

So it becomes overladen. Once a robot becomes overladen, it will spread lightning to the near one. 

The spreading happens when: 
  Robot A is overladen but robot B not. 
  The Distance between robot A and robot B is no longer than R. 
  No other robots stand in a line between them. 
In this condition, robot B becomes overladen. 

We assume that no two spreading happens at a same time and no two robots stand at a same position. 

The problem is: How many kind of lightning shape if all robots is overladen? The answer can be very large so we output the answer modulo 10007. If some of the robots cannot be overladen, just output -1. 

Input

There are several cases. 
The first line is an integer T (T < = 20), indicate the test cases. 
For each case, the first line contains integer N ( 1 < = N < = 300 ) and R ( 0 < = R < = 20000 ), indicate there stand N robots; following N lines, each contains two integers ( x, y ) ( -10000 < = x, y < = 10000 ), indicate the position of the robot.

Output

One line for each case contains the answer.

Sample Input

3
3 2
-1 0
0 1
1 0
3 2
-1 0
0 0
1 0
3 1
-1 0
0 1
1 0

Sample Output

3
1
-1

题目背景傻逼吧哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈哈、、、

判断是否在一条线上要用斜率、、、不是xy两个方向几号、、、

好像百度题解还要什么逆元什么的奇怪的东西，明明套板子就过了、、、

#include 
#include 
#include 
#include 
#include 

M - Minimum Spanning Tree

 HDU - 4408

XXX is very interested in algorithm. After learning the Prim algorithm and Kruskal algorithm of minimum spanning tree, XXX finds that there might be multiple solutions. Given an undirected weighted graph with n (1<=n<=100) vertexes and m (0<=m<=1000) edges, he wants to know the number of minimum spanning trees in the graph. 

Input

There are no more than 15 cases. The input ends by 0 0 0. 
For each case, the first line begins with three integers --- the above mentioned n, m, and p. The meaning of p will be explained later. Each the following m lines contains three integers u, v, w (1<=w<=10), which describes that there is an edge weighted w between vertex u and vertex v( all vertex are numbered for 1 to n) . It is guaranteed that there are no multiple edges and no loops in the graph. 

Output

For each test case, output a single integer in one line representing the number of different minimum spanning trees in the graph. 
The answer may be quite large. You just need to calculate the remainder of the answer when divided by p (1<=p<=1000000000). p is above mentioned, appears in the first line of each test case. 

Sample Input

5 10 12
2 5 3
2 4 2
3 1 3
3 4 2
1 2 3
5 4 3
5 1 3
4 1 1
5 3 3
3 2 3
0 0 0

Sample Output

4

最小生成树计数、、、

https://blog.csdn.net/wyfcyx_forever/article/details/40182739

是在Kruskal的基础上，每完成一个阶段（检查完一个长度），就将所有遍历过的点缩成一个点，然后用Matrix-Tree定理计算该点与下一组点组成的连通图中生成树的个数。最终把每一个阶段的结果相乘即可。

一个无向图所有的最小生成树中某种权值的边的数目均相同。（不会证明）。

然后因为相同所以枚举这个值边的当前数目的子集，能加进森林的就加，，，

最后把每个阶段的数量乘起来就好啦。

上面的删掉删掉、、、是下面那个、、、也差不多了，，，

用kruscal计算最小生成树时，每次取连接了两个不同联通块的最小的边。也就是先处理d1条c1长度的边，再处理d2条c2长度的边。长度相同的边无论怎么选，最大联通情况都是固定的。 分别对ci长度的边产生的几个联通块计算生成树数量再乘起来，然后把这些联通块缩点，再计算ci+1长度的边。

#include 
#include 
#include 
#include 
#include 

 

N - Highways

 SPOJ - HIGH

In some countries building highways takes a lot of time... Maybe that's because there are many possiblities to construct a network of highways and engineers can't make up their minds which one to choose. Suppose we have a list of cities that can be connected directly. Your task is to count how many ways there are to build such a network that between every two cities there exists exactly one path. Two networks differ if there are two cities that are connected directly in the first case and aren't in the second case. At most one highway connects two cities. No highway connects a city to itself. Highways are two-way.

Input

The input begins with the integer t, the number of test cases (equal to about 1000). Then t test cases follow. The first line of each test case contains two integers, the number of cities (1<=n<=12) and the number of direct connections between them. Each next line contains two integers a and b, which are numbers of cities that can be connected. Cities are numbered from 1 to n. Consecutive test cases are separated with one blank line.

Output

The number of ways to build the network, for every test case in a separate line. Assume that when there is only one city, the answer should be 1. The answer will fit in a signed 64-bit integer.

Example

Sample input:
4
4 5
3 4
4 2
2 3
1 2
1 3

2 1
2 1

1 0

3 3
1 2
2 3
3 1

Sample output:
8
1
1
3

生成树计数。

#include 
#include 
#include 
#include 
#include 

搞完啦！呼啦！