什么是数组?
数组对应的英文是array,是有限个相同类型的变量所组成的有序集合,数组中的每一个变量被称为元素。数组是最为简单、最为常用的数据结构。以整型数组为例,数组的存储形式如下图所示。
正如军队里的士兵存在编号一样,数组中的每一个元素也有着自己的下标,只不过这个下标从0开始,一直到数组长度-1。数组的另一个特点,是在内存中顺序存储,因此可以很好地实现逻辑上的顺序表。
数组在内存中的顺序存储,具体是什么样子呢?
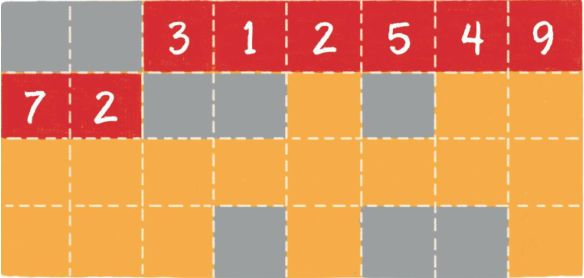
内存是由一个个连续的内存单元组成的,每一个内存单元都有自己的地址。在这些内存单元中,有些被其他数据占用了,有些是空闲的。数组中的每一个元素,都存储在小小的内存单元中,并且元素之间紧密排列,既不能打乱元素的存储顺序,也不能跳过某个存储单元进行存储。
在上图中,橙色的格子代表空闲的存储单元,灰色的格子代表已占用的存储单元,而红色的连续格子代表数组在内存中的位置。不同类型的数组,每个元素所占的字节个数也不同,本图只是一个简单的示意图。
数组读取元素和更新元素的时间复杂度都是O(1)。
数组扩容的时间复杂度是O(n),插入并移动元素的时间复杂度也是O(n),综合起来插入操作的时间复杂度是O(n)。至于删除操作,只涉及元素的移动,时间复杂度也是O(n)。
数组拥有非常高效的随机访问能力,只要给出下标,就可以用常量时间找到对应元素。有一种高效查找元素的算法叫作二分查找,就是利用了数组的这个优势。
总的来说,数组所适合的是读操作多、写操作少的场景
什么是链表?
链表是什么样子的?让我们来看一看单向链表的结构。
链表(linked list)是一种在物理上非连续、非顺序的数据结构,由若干节点(node)所组成。单向链表的每一个节点又包含两部分,一部分是存放数据的变量data,另一部分是指向下一个节点的指针next。链表的第1个节点被称为头节点,最后1个节点被称为尾节点,尾节点的next指针指向空。与数组按照下标来随机寻找元素不同,对于链表的其中一个节点A,我们只能根据节点A的next指针来找到该节点的下一个节点B,再根据节点B的next指针找到下一个节点C……这正如地下党的联络方式,一级一级,单线传递。要想让每个节点都能回溯到它的前置节点,我们可以使用双向链表。
什么是双向链表?
双向链表比单向链表稍微复杂一些,它的每一个节点除了拥有data和next指针,还拥有指向前置节点的prev指针。
如果说数组在内存中的存储方式是顺序存储,那么链表在内存中的存储方式则是随机存储。什么叫随机存储呢?
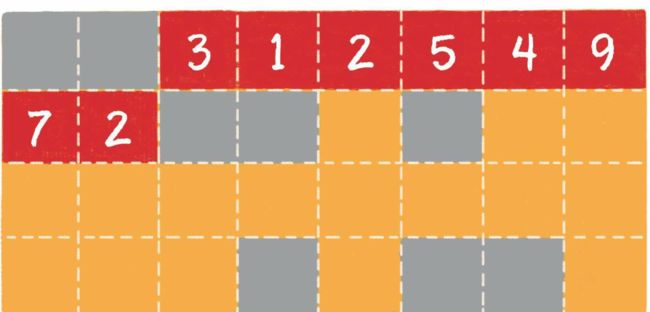
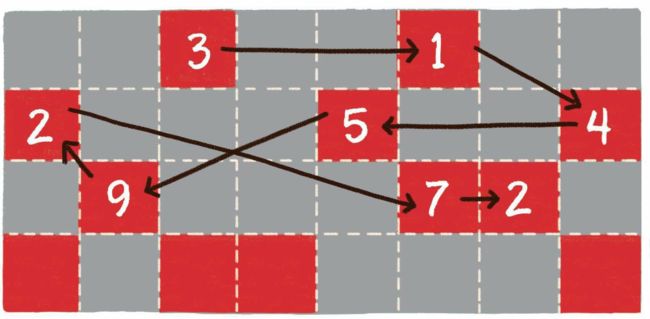
数组在内存中占用了连续完整的存储空间。而链表则采用了见缝插针的方式,链表的每一个节点分布在内存的不同位置,依靠next指针关联起来。这样可以灵活有效地利用零散的碎片空间。让我们看一看下面两张图,对比一下数组和链表在内存中分配方式的不同。
数组的内存分配方式
链表的内存分配方式
链表中的数据只能按顺序进行访问,最坏的时间复杂度是O(n)。
如果不考虑插入、删除操作之前查找元素的过程,只考虑纯粹的插入和删除操作,时间复杂度都是O(1)。
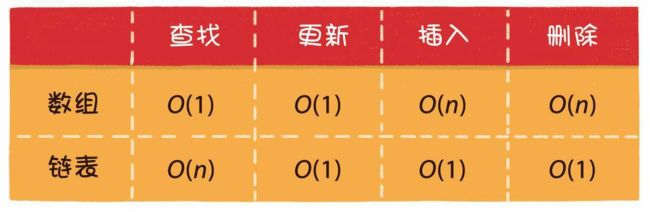
数据结构没有绝对的好与坏,数组和链表各有千秋。下面我总结了数组和链表相关操作的性能,我们来对比一下。
从表格可以看出,数组的优势在于能够快速定位元素,对于读操作多、写操作少的场景来说,用数组更合适一些。相反地,链表的优势在于能够灵活地进行插入和删除操作,如果需要在尾部频繁插入、删除元素,用链表更合适一些。
常见的数据结构有很多,但大多数都以数组或者链表作为存储方式,数组和链表可以被看作数据存储的 “物理结构”
什么是数据存储的物理结构呢?
如果把数据结构比作活生生的人,那么物理结构就是人的血肉和骨骼,看得见,摸得着,实实在在。例如我们刚刚学过的数组和链表,都是内存中实实在在的存储结构。而在物质的人体之上,还存在着人的思想和精神,它们看不见、摸不着。看过电影《阿凡达》 吗?男主角的思想意识从一个瘦弱残疾的人类身上被移植到一个高大威猛的蓝皮肤外星人身上,虽然承载思想意识的肉身改变了,但是人格却是唯一的。如果把物质层面的人体比作数据存储的物理结构,那么精神层面的人格则是数据存储的逻辑结构。逻辑结构是抽象的概念,它依赖于物理结构而存在。
- 栈和队列。这两者都属于逻辑结构,它们的物理实现既可以利用数组,也可以利用链表来完成。
- 二叉树,这也是一种逻辑结构。同样地,二叉树也可以依托于物理上的数组或链表来实现。
什么是栈?
要弄明白什么是栈,我们需要先举一个生活中的例子。假如有一个又细又长的圆筒,圆筒一端封闭,另一端开口。往圆筒里放入乒乓球,先放入的靠近圆筒底部,后放入的靠近圆筒入口。
那么,要想取出这些乒乓球,则只能按照和放入顺序相反的顺序来取,先取出后放入的,再取出先放入的,而不可能把最里面最先放入的乒乓球优先取出。
栈(stack)是一种线性数据结构,它就像一个上图所示的放入乒乓球的圆筒容器,栈中的元素只能先入后出(First In Last Out,简称FILO)。最早进入的元素存放的位置叫作栈底(bottom),最后进入的元素存放的位置叫作栈顶(top)。
栈这种数据结构既可以用数组来实现,也可以用链表来实现。
栈的数组实现如下。
栈的链表实现如下。
什么是队列 ?
要弄明白什么是队列,我们同样可以用一个生活中的例子来说明。假如公路上有一条单行隧道,所有通过隧道的车辆只允许从隧道入口驶入,从隧道出口驶出,不允许逆行。
因此,要想让车辆驶出隧道,只能按照它们驶入隧道的顺序,先驶入的车辆先驶出,后驶入的车辆后驶出,任何车辆都无法跳过它前面的车辆提前驶出。
队列(queue)是一种线性数据结构,它的特征和行驶车辆的单行隧道很相似。不同于栈的先入后出,队列中的元素只能先入先出(First In First Out,简称FIFO)。队列的出口端叫作队头(front),队列的入口端叫作队尾(rear)。与栈类似,队列这种数据结构既可以用数组来实现,也可以用链表来实现。用数组实现时,为了入队操作的方便,把队尾位置规定为最后入队元素的下一个位置。
队列的数组实现如下。
队列的链表实现如下。
队列的入队、出队操作和栈是大同小异的。但对于数组实现方式来说,队列的入队和出队操作有了一些有趣的变化。如果像这样不断出队,队头左边的空间失去作用,那队列的容量岂不是越来越小了?例如像下面这样。
用数组实现的队列可以采用循环队列的方式来维持队列容量的恒定。循环队列是什么意思呢?让我们看看下面的例子。假设一个队列经过反复的入队和出队操作,还剩下2个元素,在“物理”上分布于数组的末尾位置。这时又有一个新元素将要入队。
在数组不做扩容的前提下,如何让新元素入队并确定新的队尾位置呢?我们可以利用已出队元素留下的空间,让队尾指针重新指回数组的首位。
这样一来,整个队列的元素就“循环”起来了。在物理存储上,队尾的位置也可以在队头之前。当再有元素入队时,将其放入数组的首位,队尾指针继续后移即可。
一直到(队尾下标+1)%数组长度 = 队头下标时,代表此队列真的已经满了。需要注意的是,队尾指针指向的位置永远空出1位,所以队列最大容量比数组长度小1。
这就是所谓的循环队列。
循环队列不但充分利用了数组的空间,还避免了数组元素整体移动的麻烦,还真是有点意思呢!至于入队和出队的时间复杂度,也同样是O(1)吧
栈的应用:
栈的输出顺序和输入顺序相反,所以栈通常用于对“历史”的回溯,也就是逆流而上追溯“历史”。例如实现递归的逻辑,就可以用栈来代替,因为栈可以回溯方法的调用链。
栈还有一个著名的应用场景是面包屑导航,使用户在浏览页面时可以轻松地回溯到上一级或更上一级页面。
队列的应用:
队列的输出顺序和输入顺序相同,所以队列通常用于对“历史”的回放,也就是按照“历史”顺序,把“历史”重演一遍。
例如在多线程中,争夺公平锁的等待队列,就是按照访问顺序来决定线程在队列中的次序的。
再如网络爬虫实现网站抓取时,也是把待抓取的网站URL存入队列中,再按照存入队列的顺序来依次抓取和解析的。
那么,有没有办法把栈和队列的特点结合起来,既可以先入先出,也可以先入后出呢?这种数据结构叫作双端队列(deque)。
双端队列这种数据结构,可以说综合了栈和队列的优点,对双端队列来说,从队头一端可以入队或出队,从队尾一端也可以入队或出队。
优先队列:
还有一种队列,它遵循的不是先入先出,而是谁的优先级最高,谁先出队。
优先队列已经不属于线性数据结构的范畴了,它是基于二叉堆来实现的。
散列表:
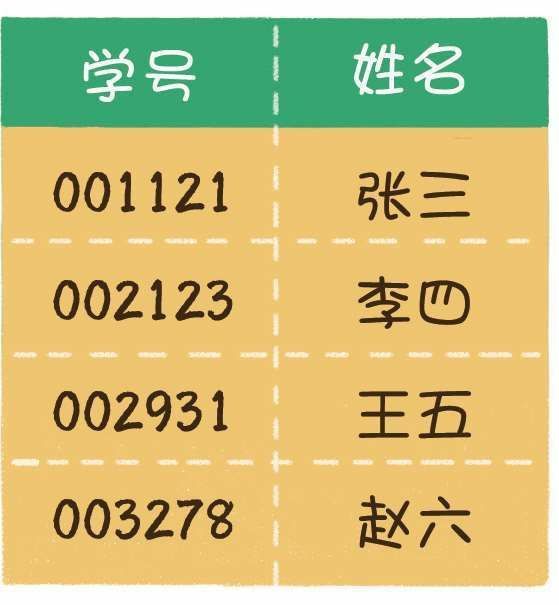
例如开发一个学生管理系统,需要有通过输入学号快速查出对应学生的姓名的功能。这里不必每次都去查询数据库,而可以在内存中建立一个缓存表,这样做可以提高查询效率。
再如我们需要统计一本英文书里某些单词出现的频率,就需要遍历整本书的内容,把这些单词出现的次数记录在内存中。
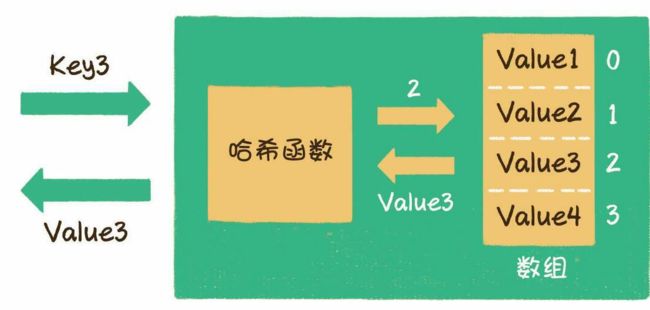
因为这些需求,一个重要的数据结构诞生了,这个数据结构叫作散列表。散列表也叫作哈希表(hash table),这种数据结构提供了键(Key)和值(Value)的映射关系。只要给出一个Key,就可以高效查找到它所匹配的Value,时间复杂度接近于O(1)。
哈希函数:
散列表在本质上也是一个数组。可是数组只能根据下标,像a[0]、a[1]、a[2]、a[3]、a[4]这样来访问,而散列表的Key则是以字符串类型为主的。
例如以学生的学号作为Key,输入002123,查询到李四;或者以单词为Key,输入by,查询到数字46……所以我们需要一个“中转站”,通过某种方式,把Key和数组下标进行转换。这个中转站就叫作哈希函数。
这个所谓的哈希函数是怎么实现的呢?在不同的语言中,哈希函数的实现方式是不一样的。这里以Java的常用集合HashMap为例,来看一看哈希函数在Java中的实现。
在Java及大多数面向对象的语言中,每一个对象都有属于自己的hashcode,这个hashcode是区分不同对象的重要标识。无论对象自身的类型是什么,它们的hashcode都是一个整型变量。
既然都是整型变量,想要转化成数组的下标也就不难实现了。最简单的转化方式是什么呢?是按照数组长度进行取模运算。index = HashCode (Key) % Array.length
实际上,JDK(Java Development Kit,Java语言的软件开发工具包)中的哈希函数并没有直接采用取模运算,而是利用了位运算的方式来优化性能。不过在这里可以姑且简单理解成取模操作。
通过哈希函数,我们可以把字符串或其他类型的Key,转化成数组的下标 index。
如给出一个长度为8的数组,则当key=001121时,index = HashCode ("001121") % Array.length = 1420036703 %8 = 7
而当key=this时,index = HashCode ("this") % Array.length = 3559070 % 8 = 6
有了哈希函数,就可以在散列表中进行读写操作
由于数组的长度是有限的,当插入的Entry越来越多时,不同的Key通过哈希函数获得的下标有可能是相同的。例如002936这个Key对应的数组下标是2;002947这个Key对应的数组下标也是2。
这种情况,就叫作哈希冲突。哈希冲突是无法避免的,既然不能避免,我们就要想办法来解决。解决哈希冲突的方法主要有两种,一种是开放寻址法,一种是链表法。
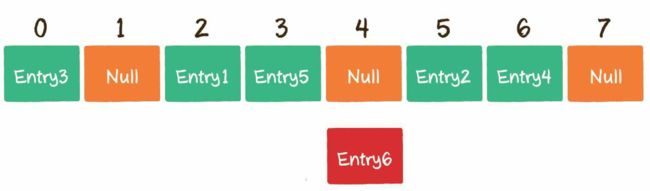
开放寻址法的原理很简单,当一个Key通过哈希函数获得对应的数组下标已被占用时,我们可以“另谋高就”,寻找下一个空档位置。以上面的情况为例,Entry6通过哈希函数得到下标2,该下标在数组中已经有了其他元素,那么就向后移动1位,看看数组下标3的位置是否有空。
很不巧,下标3也已经被占用,那么就再向后移动1位,看看数组下标4的位置是否有空。
幸运的是,数组下标4的位置还没有被占用,因此把Entry6存入数组下标4的位置。
这就是开放寻址法的基本思路。当然,在遇到哈希冲突时,寻址方式有很多种,并不一定只是简单地寻找当前元素的后一个元素,这里只是举一个简单的示例而已。在Java中,ThreadLocal所使用的就是开放寻址法。接下来,重点讲一下解决哈希冲突的另一种方法——链表法。这种方法被应用在了Java的集合类HashMap当中。
HashMap数组的每一个元素不仅是一个Entry对象,还是一个链表的头节点。每一个Entry对象通过next指针指向它的下一个Entry节点。当新来的Entry映射到与之冲突的数组位置时,只需要插入到对应的链表中即可。
当经过多次元素插入,散列表达到一定饱和度时,Key映射位置发生冲突的概率会逐渐提高。这样一来,大量元素拥挤在相同的数组下标位置,形成很长的链表,对后续插入操作和查询操作的性能都有很大影响。
这时,散列表就需要扩展它的长度,也就是进行扩容。对于JDK中的散列表实现类HashMap来说,影响其扩容的因素有两个。Capacity,即HashMap的当前长度LoadFactor,即HashMap的负载因子,默认值为0.75f衡量HashMap需要进行扩容的条件如下。
HashMap.Size >= Capacity×LoadFactor
- 扩容,创建一个新的Entry空数组,长度是原数组的2倍。
- 重新Hash,遍历原Entry数组,把所有的Entry重新Hash到新数组中。为什么要重新Hash呢?因为长度扩大以后,Hash的规则也随之改变。
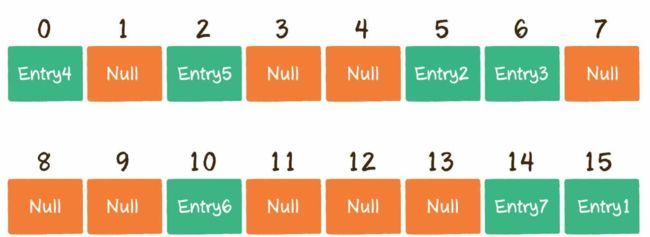
经过扩容,原本拥挤的散列表重新变得稀疏,原有的Entry也重新得到了尽可能均匀的分配。
扩容前的HashMap:
扩容后的HashMap:
需要注意的是,关于HashMap的实现,JDK 8和以前的版本有着很大的不同。当多个Entry被Hash到同一个数组下标位置时,为了提升插入和查找的效率,HashMap会把Entry的链表转化为红黑树这种数据结构。
有关 HashMap 其他详细分析参考:https://www.cnblogs.com/wuzhenzhao/p/13199350.html