BP神经网络的基础知识及MATLAB应用

BP基本知识梳理

基本概念

BP神经网络是一种信号前向传播、误差反向传播的前向有监督型学习方法。

基本原理

①以下面的模型为例：
输入层 隐藏层 输出层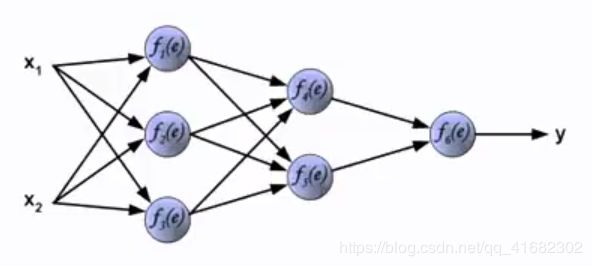
②针对每一个基本单位，即神经元，做如下计算

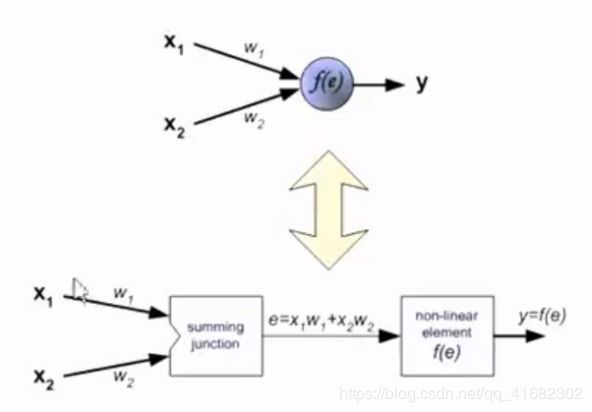
其中，x1、x2为输入数据，w1、w2为权重，计算函数f为一些特定的激活函数，y为输出数据。常见激活函数如下

利用上述方法，将数据逐层向后传递

③得到最终输出结果，并计算与实际值之间的误差

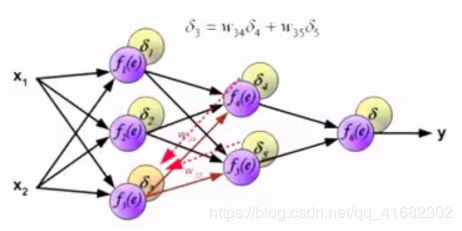
④根据权值，逐层计算误差，实现误差反向传递

⑤根据梯度下降法，逐层向后修正权值

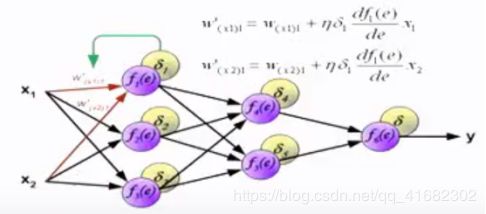
其中，η为学习率，δ为误差，δ后面的微分项为激活函数的求导
⑥循环重复②~⑤步，直至最终输出数据y与实际值之间的误差达到目标误差。

归一化

概念

归一化指的是将原始输入数据，通过函数映射到一个较为集中的区间，常见的区间例如[-1,1]、[0,1]。

目的

①加快收敛速度，速断训练时间。输入数据的单位不一样，有些数据的范围可能特别大，导致的结果是神经网络收敛慢、训练时间长。
②防止较小数据的影响因子被较大数据覆盖掉。数据范围大的输入在模式分类中的作用可能会偏大，而数据范围小的输入作用就可能会偏小。
③由于神经网络输出层的激活函数的值域是有限制的，因此需要将网络训练的目标数据映射到激活函数的值域。例如神经网络的输出层若采用S形激活 函数，由于S形函数的值域限制在(0,1)，也就是说神经网络的输出只能限制在(0,1)，所以训练数据的输出就要归一化到[0,1]区间。
④ S形激活函数在(0,1)区间以外区域很平缓，区分度太小。例如S形函数f(X)在参数a=1时，f(100)与f(5)只相差0.0067。这样数据的差异就会失去意义

归一化算法

①y = ( x - min )/( max - min ) —— [0,1]
②y = 2 * ( x - min ) / ( max - min ) - 1 —— [1,1]
（以上理论主要参考：https://blog.csdn.net/lyxleft/article/details/82840787）

MATLAB应用

题目：利用 BP 网络考察不同配比的处方，以期获得缓释制剂处方理想的释放度。考察的因素、目标及实验样本见下表
X1( A ) X2( B ) X3( C ) X4(D) Y(R.t/min)
1 1.000 2.250 3.750 2.500 63.3
2 1.125 2.750 4.750 2.000 174.4
3 1.250 3.250 3.500 1.500 14.0
4 1.375 3.750 4.500 1.000 185.7
5 1.500 2.000 3.250 2.750 99.4
6 1.625 2.500 4.250 2.250 176.6
7 1.750 3.000 3.000 1.750 142.6
8 1.875 3.500 4.000 1.250 168.2
9 2.000 4.000 5.000 3.000 121.6
将以上 9 组数据作为训练样本，为防止出现拟合不完全过早终止循环，导致输出误差过大和网络训练误差太小的过拟合两种情况，设定期望输出误差定为0.005，同时设置不同的隐层节点数，训练网络。当网络训练结束达到误差要求时，对下表中的样本进行仿真预测，把预测结果填入下表中，并由此表的预测结果，确定最佳释放度Y对应的处方配方。
X1(A) X2(B) X3© X4(D) Y(R.t/min)
1 1.0 2.0 3.0 3
2 1.2 2.4 3.4 2.6
3 1.4 2.8 3.8 2.2
4 1.6 3.2 4.2 1.8
5 1.8 3.6 4.6 1.4
6 2.0 4.0 5.0 1.0

低版本方法

%输入数据准备
factor=[1.000,2.250,3.750,2.500;1.125,2.750,4.750,2.000;1.250,3.250,3.500,1.500;1.375,3.750,4.500,1.000;1.500,2.000,3.250,2.750;1.625,2.500,4.250,2.250;1.750,3.000,3.000,1.750;1.875,3.500,4.000,1.250;2.000,4.000,5.000,3.000];
rate=[63.3;174.4;14.0;185.7;99.4;176.6;142.6;168.2;121.6];
%设置随机数序列
temp = randperm(size(factor,1));
%留一法：根据随机数序列，随机取8个训练集，1个测试集;下面的参数数据均以列的形式输入每组样本数据，因此需要转置
P_train=factor(temp(1:8),:)';
T_train=rate(temp(1:8),:)';
P_test=factor(temp(9),:)';
T_test=rate(temp(9),:)';
%训练数据归一化，低版本用premnmx函数
[p_train,minp,maxp,t_train,mint,maxt]=premnmx(P_train,T_train);
%构建神经网络 [输入层神经元个数，隐层神经元个数，输出层神经元个数]
net=newff(minmax(P_train),[4,3,1],{'tansig','tansig','purelin'},'trainlm');
net.trainParam.epochs=1000;
net.trainParam.goal=0.005;
net.trainParam.lr = 0.01 ;
%训练网络
net=train(net,p_train,t_train);
%测试数据归一化，需要使用跟训练数据归一化相同的预处理
p_test=tramnmx(P_test,minp,maxp);
%仿真
t_sim=sim(net,p_test);
%反归一化得到仿真结果
T_sim=postmnmx(t_sim,mint,maxt);
%判断误差
error=abs(T_sim-T_test)./T_test
%预测
P_result=[1.0,2.0,3.0,3;1.2,2.4,3.4,2.6;1.4,2.8,3.8,2.2;1.6,3.2,4.2,1.8;1.8,3.6,4.6,1.4;2.0,4.0,5.0,1.0]';
p_result=tramnmx(P_result,minp,maxp);
t_result=sim(net,p_result);
T_result=postmnmx(t_result,mint,maxt)

训练结果图：

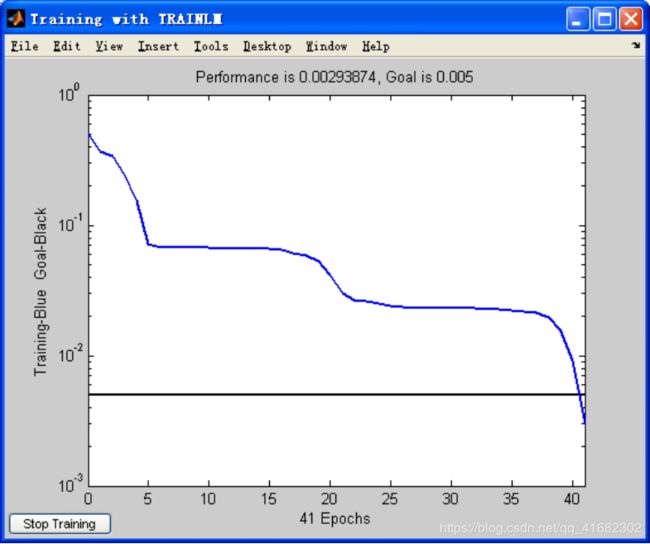
预测结果：
error=
0.041437
T_result =
97.5586 54.2094 176.5992 181.5865 149.3388 115.1088

高版本方法

%输入数据准备
factor=[1.000,2.250,3.750,2.500;1.125,2.750,4.750,2.000;1.250,3.250,3.500,1.500;1.375,3.750,4.500,1.000;1.500,2.000,3.250,2.750;1.625,2.500,4.250,2.250;1.750,3.000,3.000,1.750;1.875,3.500,4.000,1.250;2.000,4.000,5.000,3.000];
rate=[63.3;174.4;14.0;185.7;99.4;176.6;142.6;168.2;121.6];
%设置随机数序列
temp = randperm(size(factor,1));
%留一法：根据随机数序列，随机取8个训练集，1个测试集;下面的参数数据均以列的形式输入每组样本数据，因此需要转置
P_train=factor(temp(1:8),:)';
T_train=rate(temp(1:8),:)';
P_test=factor(temp(9),:)';
T_test=rate(temp(9),:)';
N=size(P_test,2);
%训练数据归一化，高版本用mapminmax函数，函数返回结果为[归一化后的数据,归一化处理因子]，“归一化处理因子”使预测数据归一化时与使用相同的归一化处理
[p_train,ps_input]=mapminmax(P_train);
[t_train,ps_output]=mapminmax(T_train);
%构建神经网络 newff(输入数据，输出数据，隐藏神经元个数)
net=newff(p_train,t_train,10);
net.trainParam.epochs=1000;
net.trainParam.goal=0.005;
net.trainParam.lr = 0.01 ;
%训练网络
net=train(net,p_train,t_train);
%测试数据归一化，需要使用跟训练数据归一化相同的预处理
p_test=mapminmax(‘apply’,P_test,ps_input);
%仿真
t_sim=sim(net,p_test);
%反归一化得到仿真结果，同样要使用训练数据中结果数据归一化同样的预处理
T_sim=mapminmax(‘reverse’,t_sim,ps_output);
%判断误差
error=abs(T_sim-T_test)./T_test
%预测
P_result=[1.0,2.0,3.0,3;1.2,2.4,3.4,2.6;1.4,2.8,3.8,2.2;1.6,3.2,4.2,1.8;1.8,3.6,4.6,1.4;2.0,4.0,5.0,1.0]';
p_result=tramnmx(P_result,minp,maxp);
t_result=sim(net,p_result);
T_result=postmnmx(t_result,mint,maxt)

训练结果图

预测结果：
T_result =
41.1775 91.5617 167.6867 183.1601 184.0594 183.1458