2020杭电多校第四场 1004 Deliver the Cake

题目

题目链接

题目大意是：
给定一张无向有权图，已知其起点和终点，每个节点有方向LR或M。蛋糕每次换手需要一定时间x。在方向为L或R的节点，蛋糕必须在对应的手上，而方向为M的地方则无所谓。

问最终从起点到终点的最短路程是多少。

拆点+最短路

这道题，一步一步的来分析

第一步，如果没有对点的方向限制，将会是一个非常简单的最短路问题。现在有了方向限制。

第二步，假设当前仅有左右两种方向的限制。那么问题也会变得简单只需要将两端方向不一样的边权加上x，这样就没有了方向限制，跑第一步即可。

第三步，考虑到存在方向为M的点，可以将其看作是两个点，一个是方向为左的点一个是方向为右的点，将其拆开，与周围的点重新建边。

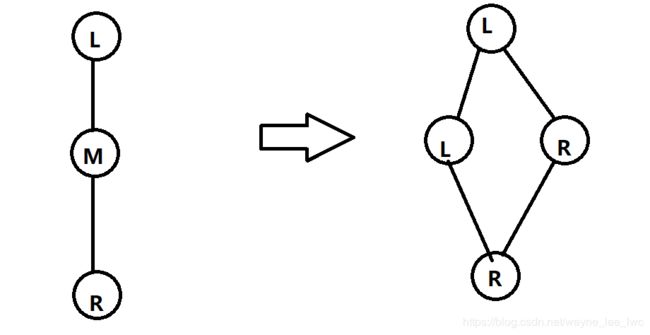
经过这样一顿操作，图中就没有方向为M的点了，剩下的图就只剩下方向为左或者右的点了，按照刚刚第二步分析的那样实现就好。

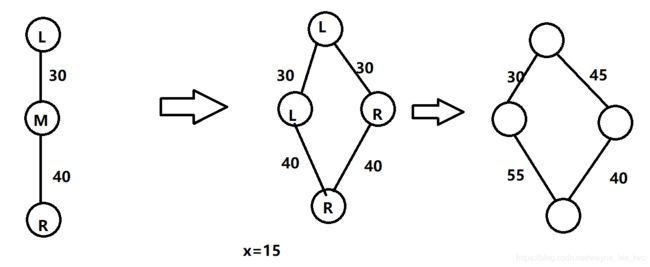
需要注意的是，这里拆点可能会造成边的数量很多，建议开10被的m。

另外，起点和终点有可能被拆成两个顶点，为了不跑多次最短路，可以建造一个虚拟起点和终点分别向拆开的起点和终点连接长度为0的边。

代码：

#include
#include
#include
using namespace std;
const int M = 1000060;
const int N = 1000060;
struct E{
    int point;
    int next;
    long long dis; 
}nxt[M];
struct Node{
    int po;
    long long dis;
    
    bool operator < (const Node& o)const{
        return dis > o.dis;
    }
};

priority_queue<Node> q;
int head[N];
int dir[N];
int T,n,m,s1,s2,t1,t2,x,tot,s,t;
char dirC[N];
bool vis[N];

void link(int a,int b,long long dis){
    nxt[++tot] = {b,head[a],dis};
    head[a] = tot;
}

void dfs1(int k){
    vis[k] = true;
    if(dir[k] == 0){
        n++;
        vis[n] = true;
        dir[k] = -1;
        dir[n] = 1;
        
        if(k == s1)s2 = n;
        if(k == t1)t2 = n;
        
        for(int i = head[k],j;i;i = nxt[i].next){
            j = nxt[i].point;
            link(j,n,nxt[i].dis);
            link(n,j,nxt[i].dis);
        }
    }
    for(int i = head[k],j;i;i = nxt[i].next){
        if(vis[nxt[i].point])
            continue;
        dfs1(nxt[i].point);
    }
}

void dfs2(int k){
    vis[k] = true;
    for(int i = head[k];i;i = nxt[i].next){
        nxt[i].dis += (dir[k] != dir[nxt[i].point]) * x;
    }
    for(int i = head[k];i;i = nxt[i].next){
        if(vis[nxt[i].point])
            continue;
        dfs2(nxt[i].point); 
    }
}

void clearVis(){
    for(int i = 1;i <= n;i++){
        vis[i] = false;
    }
}

long long dijkstar(){
    clearVis();
    q.push({s,0});
    
    Node o;
    while(!q.empty()){
        o = q.top();
        q.pop();
        if(vis[o.po]) continue;
        
        if(o.po == t) return o.dis;
        
        vis[o.po] = true;
        
        for(int i = head[o.po],j;i;i = nxt[i].next){
            j = nxt[i].point;
            if(vis[j])    continue;
            q.push({j,o.dis + nxt[i].dis});
        }
    }
}

int main(){
    for(cin >> T;T;T--){
        tot = 0;s2 = t2 = 0; 
        t = s = 0;
        while(!q.empty()) q.pop();
        scanf("%d%d%d%d%d",&n,&m,&s1,&t1,&x);
        scanf("%s",dirC + 1);
        
        for(int i = 1;i <= n;i++){
            
            if(dirC[i] == 'R')
                dir[i] = 1;
            if(dirC[i] == 'L')
                dir[i] = -1;
            if(dirC[i] == 'M')
                dir[i] = 0;
        }
        
        for(int i = 1;i <= n << 1;i++)    head[i] = 0;
            
        for(int i = 1,a,b,dis;i <= m;i++){
            scanf("%d%d%d",&a,&b,&dis);
            link(a,b,dis);
            link(b,a,dis);
        }
        clearVis();
        dfs1(s1);
        s = ++n;t = ++n;
        
        clearVis();
        dfs2(s1);
        if(s2)    dfs2(s2);
                
        link(s,s1,0);
        if(s2)    link(s,s2,0);
        link(t1,t,0);
        if(t2)    link(t2,t,0);
        cout << dijkstar() << endl;
        
    }
}