CVX介绍——基础篇

CVX的介绍主要是记录CVX的使用文件：http://web.cvxr.com/cvx/doc/intro.html#what-is-disciplined-convex-programming 中的一些语法，以待将来查阅，其安装以及简单的案例可以在文件A quick start中找到，很简单，这里就不赘述了。

首先，所有CVX模型都必须以命令cvx_begin开头，并以命令cvx_end结束。 所有的变量声明，目标函数和约束都应该介于两者之间。 cvx_begin命令可能包含更多的修饰符：
cvx_begin quiet
防止模型在解算时产生任何屏幕输出。
cvx_begin sdp
调用半确定编程模式。
cvx_begin gp
调用几何编程模式。
这些修饰剂可以在适当的时候结合使用; 例如，cvx_begin sdp quiet会调用SDP模式并使求解器输出无效。

变量
CVX的变量可以是实数或复数标量，向量，矩阵或n维数组。例如

variable X
variable Y(20,10)
variable Z(5,5,5)

就分别定义了一个标量X，一个20×10的矩阵Y（包含200个标量变量）和一个5×5×5的数组Z（包含125个标量变量）。
变量声明还可以包含一个或多个关键字来表示变量上的各种结构或条件。 例如，要声明一个复杂的变量，可以使用复杂的关键字：

variable w(50) complex

非负变量和对称/埃尔米特半正定（PSD）矩阵可分别用非负半定义关键字指定：

variable x(10) nonnegative
variable Z(5,5) semidefinite
variable Q(5,5) complex semidefinite

对于MIDCP，整数和二进制关键字分别用于声明整数和二进制变量：

variable p(10) integer
variable q binary

各种关键字可用于帮助构造具有矩阵结构的变量，例如对称性或带状（关于带状矩阵可参考http://blog.sina.com.cn/s/blog_54f1857701000a33.html）。 例如，下面代码段就声明Y是一个实的50×5050×50对称矩阵变量，Z a 100×100100×100 Hermitian Toeplitz矩阵变量。 （注意，hermitian关键字也指定矩阵是复杂的。）

variable Y(50,50) symmetric
variable Z(100,100) hermitian toeplitz

当前支持的结构关键字是：

banded(lb,ub)      diagonal           hankel             hermitian
skew_symmetric     symmetric          toeplitz           tridiagonal
lower_bidiagonal   lower_hessenberg   lower_triangular
upper_bidiagonal   upper_hankel       upper_hessenberg   upper_triangular

下划线实际上可以省略,lower triangular这种写法也可以。
这些关键字大部分意义都很明确，但也有一些例外：

banded(lb,ub)

该矩阵以较低的带宽lb和较高的带宽ub进行带限。 如果lb和ub均为零，则产生对角矩阵。 ub可以省略，在这种情况下，它被设置为等于lb.例如，带状（1,1）（或带状（1））是三对角矩阵。

upper_hankel

矩阵是Hankel，并且在中心对角线以下，即对于i + j> n + 1为零。
当提供多个关键字时，得到的矩阵结构由交集确定。 例如，对称三角对称是一个有效的组合。 也就是说，在这种情况下，当一个更合理的选择存在时，CVX确实拒绝了对称的lower_triangular这样的组合。 而且，如果关键字完全冲突，那么将会导致满足所有关键字的emph {no}非零矩阵。
特定于矩阵的关键字也可以应用于n维数组：数组中的每个二维“切片”都被赋予所述的结构。 例如，声明

variable R(10,10,8) hermitian semidefinite

构造了8个10×10复Hermitian PSD矩阵，存储在R的2-D切片中（这里也许我理解有误）。

CVX变量语句非常灵活，单它只能用于声明单个变量，如果要声明很多变量，这可能不方便。 出于这个原因，提供了变量语句，允许您声明多个变量;即，

variables x1 x2 x3 y1(10) y2(10,10,10);

变量命令的一个限制是它不能声明复杂的，整型的或结构化的变量。 这些必须使用单数变量命令一次一个地声明。

目标函数
声明一个目标函数需要使用最小化函数或最大化函数。调用中最小化的目标函数必须是凸的，最大化的目标函数必须是凹的; 例如：

minimize( norm( x, 1 ) )maximize( geo_mean( x ) )

至多有一个目标函数可以在CVX规范中声明，并且它必须有一个标量值。

如果没有指定目标函数，则该问题被解释为可行性问题，这与将目标函数设置为零来执行最小化相同。 在这种情况下，如果找到可行点，则cvx_optval或者是0，如果约束不可行，则为+ Inf。

约束
CVX支持以下约束类型：

等号==约束，其中左侧和右侧都是仿射表达式。
小于<=不等式约束，其中左边的表达式是凸的，右边的表达式是凹的。
大于> =约束，其中左边的表达式是凹的，右边的表达式是凸的。
不等于运算符〜=可能永远不能用在约束中; 在任何情况下，这样的约束都很少凸起。 CVX的最新版本现在允许不等链接在一起; 例如1 <= x <= u。 （以前的版本不允许链接不平等。）
请注意单个等于=，这是一个赋值，和双等于==，它表示相等之间的重要区别; 有关此区别的更多信息，请参阅 Assignment and expression holders 。

严格的不平等也被接受，但是它们的解释与它们的非严格的同类相同。 我们强烈建议不要使用它们，未来版本的CVX可能会将其彻底删除。 它的推理，请看document中的Strict inequalities。

不等式和等式约束以元素的方式应用，匹配MATLAB本身的行为。 例如，如果A和B是m×n矩阵，则A <= B被解释为mn（标量）不等式A（i，j）<= B（i，j）。 当一方或另一方是标量时，该值就被复制了; 例如，A> 0被解释为A（i，j）> = 0。
不等式的元素处理在半定规划模式中被改变; 请参阅document中的semidefinite programming mode。

CVX还支持设置的成员约束; 请参阅下面的设置成员。

函数
基本CVX函数库包含各种凸，凹和仿射函数，它们接受CVX变量或表达式作为参数。 许多常用的Matlab函数，如sum，trace，diag，sqrt，max和min，根据需要重新实现以支持CVX; 其他的是在Matlab中找不到的新功能。 Reference guide中提供了基础库中功能的完整列表。 也可以添加自己的新功能; 请参阅document中的 Adding new functions to the atom library。

基础库中函数的一个示例是二次超线性函数quad_over_lin：

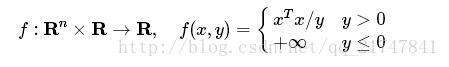
（该函数也接受复数x，但我们将考虑实数x使事情变得简单。）二次超线性函数在x和y中是凸的，因此可以作为一个目标，适当的约束，或更复杂的表达 。 例如，我们可以使（Ax-b，cTx + d）的二次超线性函数最小化，使用

minimize( quad_over_lin( A * x - b, c' * x + d ) );

在CVX规范中，假设x是向量优化变量，A是矩阵，b和c是向量，d是标量。 CVX认识到这个客观表达式是一个凸函数，因为它是一个具有仿射函数的凸函数（二次超线性函数）的组合。
您也可以在CVX规范之外使用函数quad_over_lin。 在这种情况下，它只是计算（数值）给定（数值）参数。 如果c’* x + d是正数，则结果在数值上等于tp

( ( A * x - b )' * ( A * x - b ) ) / ( c' * x + d )

但是，quad_over_lin函数也执行域检查，所以如果c’* x + d为零或负数，它将返回Inf。

设置成员
CVX支持凸集的定义和使用。 基库包括正半定n×n矩阵的锥，二阶或洛伦兹锥，以及各种规范球。 集合中给出了在基础库中提供的集合的完整列表。

不幸的是，Matlab语言没有一个集合运算符，如S中的x来表示x∈Sx∈S。 所以在CVX中，我们使用稍微不同的语法来要求表达式在一个集合中。 为了表示一个集合，我们使用一个返回一个未命名的变量的函数，该变量需要在集合中。 考虑例如，对称正半定n×n矩阵的锥。 在CVX中，我们用函数semidefinite（n）来表示这个函数，它返回一个未命名的新变量，它被约束为正半定。 为了要求矩阵表达式X是对称正半定，我们使用语法

X == semidefinite(n)

这个字面上的意思是，X被约束成等于一个未命名的变量，它必须是一个n×n对称正半定矩阵。 这当然相当于说X必须是对称正半定的。

作为例子，考虑（矩阵）变量X是相关矩阵的约束，即它是对称的，具有单位对角元素，并且是正半定。 在CVX中，我们可以声明这样一个变量，并使用这些约束

variable X(n,n) symmetric;
X == semidefinite(n);
diag(X) == 1;

这里的第二行强制X是正半定的约束。 （你可以在这里读取“==”作为“is”或“is in”，所以第二行可以被读为X是正半定值）。第三行的左边是一个包含X的对角线元素的向量 ，其要素我们要求等于一个。

如果这种使用等式约束来表示集合成员资格仍然令人困惑或者仅仅在美学上令人不快，我们已经创建了一个“伪运算符”，您可以使用它。 所以，例如，上面的半定义约束可以被替换为

X <In> semidefinite(n);

这与使用等式约束运算符完全等价，但如果您觉得它更令人愉快，则可以随意使用它。 实现这个操作符需要一些Matlab的技巧，所以不要指望能够在CVX模型之外使用它。

集合可以在仿射表达式中组合，并且我们可以将仿射表达式约束在凸集合中。 例如，我们可以强加一个表单的约束

A*X*A'-X  B*semidefinite(n)*B';

其中X是n×n对称变量矩阵，A和B是nn×n个常数矩阵。 这个约束要求，对于某些。

CVX还支持其元素是有序数量列表的集合。 作为一个例子，考虑二阶或洛伦兹锥，

epi表示一个函数的铭文。 Qm的一个元素是一个有序列表，有两个元素：第一个是mm向量，第二个是标量。 我们可以使用这个锥来表示最小二乘问题（以相当复杂的方式）的简单最小二乘问题，如下所示：

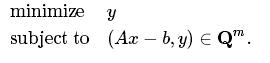
CVX使用Matlab的单元阵列工具来模拟这种表示法：

cvx_begin
    variables x(n) y;
    minimize( y );
    subject to
        { A*x-b, y }  lorentz(m);
cvx_end

函数调用lorentz（m）返回一个未命名的变量（即由一个向量和一个标量变量组成的一对），被约束在长度为m的洛伦兹锥中。 所以本规范中的约束要求对{A * x-b，y}位于适当大小的洛伦兹锥中。

双变量
当一个disciplined凸规划解决了，相关的双重问题也解决了。 （在这种情况下，原始问题被称为原始问题）。最优对偶变量，每一个都与原始问题中的约束相关联，给出关于原始问题的有价值的信息，例如关于扰动的敏感性 约束（比较凸面优化，第5章）。 为了访问CVX中的最佳双变量，只需声明它们，并将它们与约束关联即可。 考虑，例如，LP

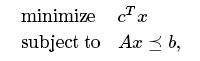
变量x∈Rn，m不等式约束。 为了将这个双变量y与这个LP中的不等式约束Ax⪯b相关联，我们使用下面的语法：

n = size(A,2);
cvx_begin
    variable x(n);
    dual variable y;
    minimize( c' * x );
    subject to
        y : A * x <= b;
cvx_end

dual variable y;

告诉CVX，y代表双变量

y : A * x <= b;

将其与不平等约束联系起来。 注意冒号操作符是如何以不同于标准的Matlab的方式被使用的，在标准的Matlab中它用来构造数字序列，如1:10。 这种新的行为只有在存在双重变量时才有效，所以不应该有混淆或冲突。 y没有给出尺寸; 它们是根据它所关联的约束自动确定的。 例如，如果m = 20，则在紧接在cvx_end之前在Matlab命令提示符处键入y

y =
    cvx dual variable (20x1 vector)

没有必要将双变量放在约束的左侧; 例如，上面的行也可以这样写：
A * x <= b : y;
另外，不平等约束的双变量总是非负的，这意味着不平等的意义可以被颠倒而不改变双变量的值;即

b >= A * x : y;

产生相同的结果。 另一方面，对于等式约束，交换等式约束的左侧和右侧将会否定双变量的最优值。
处理完cvx_end语句后，假设优化成功，CVX分别给x和y分配数值，分别是最优的原始和双重变量值。 该LP的最优原始和双重变量必须满足互补松弛条件

你可以用Matlab在Matlab中检查

y .* (b-A*x)

它打印出y和b-A * x的条目的乘积，应该几乎为零。 这行必须在cvx_end命令（将数字值赋给x和y）之后执行。 如果它在CVX规范里执行，那么它会产生一个错误，其中y和b-A * x仍然只是抽象表达式。
如果优化不成功，因为问题是不可行的或无限的，那么x和y将会有不同的值。 在无界的情况下，x将包含无限的方向; 即满足的点x

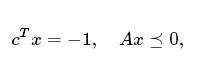
y就会被NaN值填满，反映出双重问题是不可行的。 在不可行的情况下，x充满了NaN值，而y则包含无限的双向; 即满足的点y

当然，原始和双重点和/或方向的精确解释取决于问题的结构。 有关双重信息的解释，请参阅凸凸优化等参考资料。

CVX还支持索引双变量的声明。 当模型中约束的数量（以及因此双变量的数量）取决于参数本身时，这些证明是有用的。 有关索引双变量的更多信息，请参见索引 Indexed dual variables。

Assignment and expression holders
任何具有C或Matlab经验的人都能理解单等于赋值运算符=和双等号运算符==之间的差别。 这种区别在CVX中也非常重要，而CVX则采取措施确保分配不被不恰当地使用。 例如，请考虑以下代码片段：

variable X(n,n) symmetric;
X = semidefinite(n);

乍一看，声明X = semidefinite（n）; 可能看起来像约束X是正半定的。 但是由于使用赋值运算符，X实际上被匿名半定义变量覆盖。 幸运的是，CVX禁止以这种方式覆盖声明的变量; 当达到cvx_end时，这个模型会发出以下错误：

??? Error using ==> cvx_end
The following cvx variable(s) have been overwritten:
   X
This is often an indication that an equality constraint was
written with one equals '=' instead of two '=='. The model
must be rewritten before cvx can proceed.

我们希望这个检查能够防止至少一些印刷错误在你的模型中产生令人沮丧的结果。

尽管有这个警告，任务还是真正有用的，所以我们鼓励他们适当的使用。 例如，考虑下面的摘录：

variables x y
z = 2 * x - y;
square( z ) <= 3;
quad_over_lin( x, z ) <= 1;

构造z = 2 * x - y不是一个等式约束; 这是一个任务。 它存储一个中间计算2 * x - y，这是一个仿射表达式，稍后在两个不同的约束中使用。 我们称z为表达式持有者，将其与正式声明的CVX变量区分开来。
将一组表达式累加到一个单独的Matlab变量中通常是有用的。 不幸的是，在这种情况下，Matlab对象模型的一些技术细节可能会导致问题。 考虑这个结构：

variable u(9);
x(1) = 1;
for k = 1 : 9,
    x(k+1) = sqrt( x(k) + u(k) );
end

这似乎足够合理：x应该是一个向量，其第一个值是1，其后续值是凹面的CVX表达式。 但是如果你在CVX模型中尝试这个，Matlab会给你一个相当神秘的错误(龟龟还神秘错误)：

??? The following error occurred converting from cvx to double:
Error using ==> double
Conversion to double from cvx is not possible.

出现这种情况的原因是当赋值x（1）= 1时，Matlab变量x被初始化为一个数值数组; 而Matlab将不允许随后将CVX对象插入数值数组中。
解决的办法是在给它赋值之前显式声明x是表达式的持有者。 我们为此提供了关键字表达式和表达式，用于声明单个或多个表达式持有者以供将来分配。 一旦声明表达式持有者，您可以自由地插入数字和CVX表达式。 例如，前面的示例可以更正如下：

variable u(9);
expression x(10);
x(1) = 1;
for k = 1 : 9,
    x(k+1) = sqrt( x(k) + u(k) );
end

CVX将无误地接受这个构造。 然后可以用任何适当的方式使用凹面表达式x（1），…，x（10）; 例如，你可以最大化x（10）。

变量对象和表达式对象之间的区别是相当重要的。 变量对象包含优化变量，不能在CVX规范中覆盖或分配。 （然而，在解决问题之后，CVX会用最优值覆盖优化变量）。另一方面，表达式对象被初始化为零，应该被认为是临时存放CVX表达式的地方; 它可以分配给，自由重新分配，并覆盖在CVX规范。

当然，正如我们的第一个例子所显示的那样，在创建或使用表达式之前并不总是需要声明它。 但是这样做为模型提供了额外的清晰度，所以我们强烈推荐它。