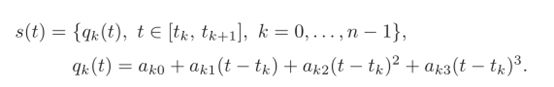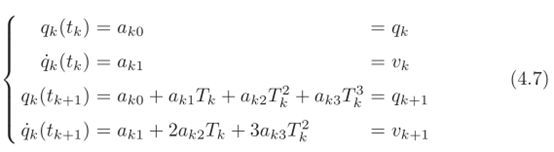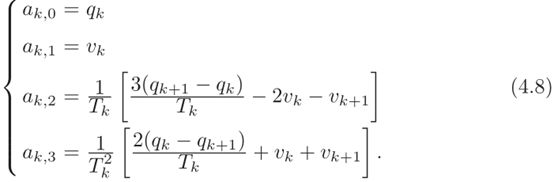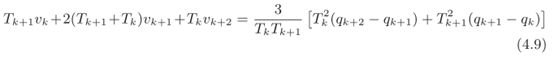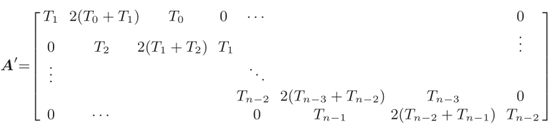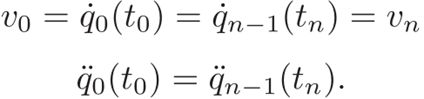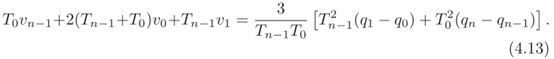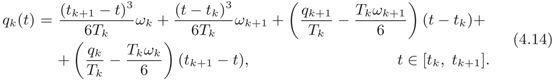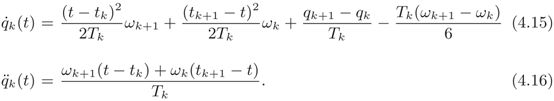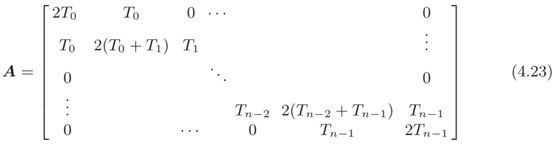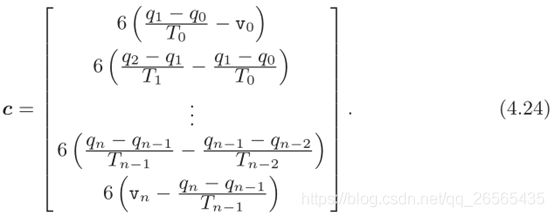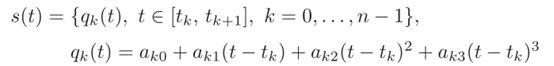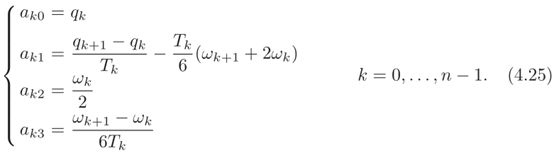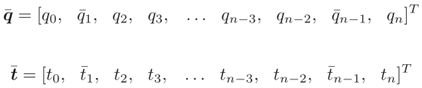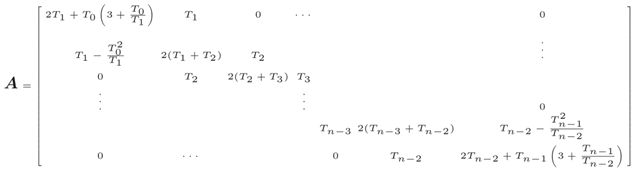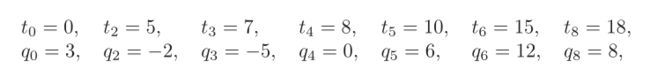机器人轨迹规划:三次样条曲线
机器人轨迹规划:三次样条曲线
文章目录
- 机器人轨迹规划:三次样条曲线
- 写在前面
- 三次样条曲线性质
- 当指定初始速度v0和最终速度vn时的参数计算(也就是v0和vn已知)
- 例子
- 周期三次样条:没有指定初始速度v0和最终速度vn(也就是v0和vn未知)
- 例子
- 具有指定初始速度v0和最终速度vn的三次样条(v0和vn已知):基于加速度的计算
- 具有指定初始、最终速度以及加速度的三次样条曲线
- 例子
- 参考文献(实际上我就是翻译了一下下。。。)
写在前面
在一些避障的应用场景下,一般都是先在任务空间中对多轴机械臂的末端进行路径规划,得到的是末端的运动路径点数据。这条轨迹只包含位置关系,并没有告诉机器人应该以怎样的速度、加速度运动,这就需要进行带时间参数的轨迹规划处理,也就是对这条空间轨迹进行速度、加速度约束,并且计算运动到每个路点的时间,高级的算法有TOPP等,一般的呢就是贝塞尔、三次准/非/均匀B、五次及三次样条等。下面从最简单的三次样条开始讨论。
三次样条曲线性质
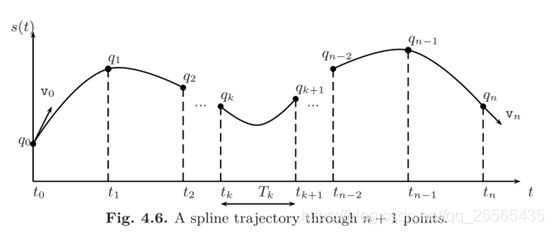
当给出n+1个点时,可以使用n个p次多项式(通常较低)代替唯一的n次插值多项式,每个多项式定义一段轨迹。以这种方式定义的总函数s(t)称为p阶的样条曲线。p的值是根据所需的样条连续度来选择的。例如,为了在两个连续段之间发生过渡的时刻tk获得速度和加速度的连续性,可以假定多项式的阶数p=3(三次多项式)。
定义三次样条曲线的函数形式为:
这段轨迹由n个三次多项式构成,并且每个多项式需要计算四个参数。由于n个多项式是定义一条通过n+1点的轨迹所必需的,因此需要确定的系数总数为4n。为了解决这个问题,必须考虑以下条件:
-
给定点插值的2n条件,因为每一个三次函数必须在其极值处穿过点。
-
n-1个条件,过渡点的速度要连续;
-
n-1个条件,过渡点的加速度要连续;
这样的话,就已经限制了2n+2(n-1)个条件,还剩下2个自由度还未限制。通过前面分析,还需要两个限制条件才行,这里讨论的就是初始点和终点的速度以及加速度。下面是几种可能的选择,可以任意选择:
-
如图4.6所示,初始速度 s ˙ ( t 0 ) = v 0 \dot{s}\left(t_{0}\right)=v_{0} s˙(t0)=v0,终止速度 s ˙ ( t n ) = v n \dot{s}\left(t_{n}\right)=v_{n} s˙(tn)=vn;
-
自然条件下, 初始加速度和最终加速度 s ¨ ( t 0 ) , s ¨ ( t n ) \ddot{s}\left(t_{0}\right), \ddot{s}\left(t_{n}\right) s¨(t0),s¨(tn)均为0;
-
当需要定义周期T=tn-t0这样的样条曲线时,条件 s ˙ ( t 0 ) = s ˙ ( t n ) \dot{s}\left(t_{0}\right)=\dot{s}\left(t_{n}\right) s˙(t0)=s˙(tn)、 s ¨ ( t 0 ) = s ¨ ( t n ) \ddot{s}\left(t_{0}\right)=\ddot{s}\left(t_{n}\right) s¨(t0)=s¨(tn)被使用;
-
t1和tn-1时刻时jerk连续,表现为:
通常情况,样条曲线具有如下几个特性:
-
对于由给定点(tk,qk),k=0,…n得到的p阶样条曲线s(t),[n(p+1)]个参数可以确定
-
给定n+1个点,并且给定边界条件,则p阶插值样条曲线s(t)能被唯一确定
-
用于构造样条曲线的多项式的阶数p不取决于数据点的数目
-
函数s(t)p-1阶连续可导
-
自然样条曲线是指初始加速度和最终加速度均为0的样条曲线
当指定初始速度v0和最终速度vn时的参数计算(也就是v0和vn已知)
在定义自动机械的轨迹时,速度剖面的连续性条件至关重要。因此,计算样条曲线的典型选择是指定初始和最终速度v0和vn。因此,给定点(tk,qk),k=0,…n以及速度的边界条件(初始速度和最终速度)v0,vn,就有如下几个条件成立:
可以最终确定样条曲线的函数s(t)为
系数ak,i可以由以下算法进行确定:
第一种情况,如果中间点(插补点)的速度我们已知,也就是vk,k=1,…,n-1,对于每段三次样条曲线,有
其中, T k = t k + 1 − t k T_{k}=t_{k+1}-t_{k} Tk=tk+1−tk。通过解上面的方程,可以得到
这就可以把每一段曲线的系数都求出来,从而得到样条曲线。这是最简单的情况!
子函数如下:
% 三次样条:指定初始速度v0和终止速度vn,并且中间插补点的速度已知,这是最简单的情况
% Input:
% q:给定点的位置
% t:给定点位置对应的时间
% v:包括给定起始、中间及终止速度的速度向量
% tt:插补周期
% Output:
% yy dyy ddyy:样条曲线函数值、速度、加速度值
function [yy dyy ddyy] = cubicSpline_1(q, t, v, tt)
if length(q) ~= length(t)
error('输入的数据应成对')
end
n = length(q);
T = t(n) - t(1); % 运行总时长
nn = T / tt; % 总点数
yy = zeros(1, nn);
dyy = zeros(1, nn);
ddyy = zeros(1, nn);
j = 1;
for i = 1: n-1
Tk = t(i+1) - t(i);
a0 = q(i);
a1 = v(i);
a2 = (1/Tk) * ((3*(q(i+1)-q(i)))/Tk - 2*v(i) - v(i+1));
a3 = (1/(Tk*Tk)) * ((2*(q(i)-q(i+1)))/Tk + v(i) + v(i+1));
for tk = t(i): tt: t(i+1)
if i > 1 && tk == t(i)
continue
end
yy(j) = a0 + a1*(tk-t(i)) + a2*power(tk-t(i), 2) + a3*power(tk-t(i), 3);
dyy(j) = a1 + 2*a2*(tk-t(i)) + 3*a3*power(tk-t(i), 2);
ddyy(j) = 2*a2 + 6*a3*(tk-t(i));
j = j + 1;
end
end
end
第二种情况,如果中间点的速度我们未知,也就是vk,k=1,…,n-1均未知,然而这些值是必须被计算的。为此,考虑了中间加速度的连续条件:
![]()
在这些条件下,通过考虑参数 a k , 2 , a k , 3 , a k + 1 , 2 a_{k, 2}, \quad a_{k, 3}, \quad a_{k+1,2} ak,2,ak,3,ak+1,2的表达式乘以 ( T k T k + 1 ) / 2 \left(T_{k} T_{k+1}\right) / 2 (TkTk+1)/2,在简单计算整理之后能够得到
其中k=0,…,n-2。
上面的关系可以整理成矩阵的形式, A ′ v ′ = c ′ A^{\prime} v^{\prime}=c^{\prime} A′v′=c′,其中
其中常数项ck仅取决于中间位置和已知的样条曲线段的持续时间Tk。由于速度v0和vn也是已知的,所以可以消除矩阵A‘的相应列并获得
也就是
其中, T = [ T 0 , T 1 , … , T n − 1 ] T , q = [ q 0 , q 1 , … , q n − 1 ] T T=\left[T_{0}, T_{1}, \ldots, \mathrm{T}_{n-1}\right]^{T}, \quad q=\left[q_{0}, \mathrm{q}_{1}, \ldots, \mathrm{q}_{n-1}\right]^{T} T=[T0,T1,…,Tn−1]T,q=[q0,q1,…,qn−1]T。A具有对角占优结构,这就转化成求解系数矩阵为对角占优的三对角线方程组的问题,普通就是利用追赶法求解>。因此,如果 T k > 0 ( ∣ a k k ∣ > ∑ j ≠ k ∣ a k j ∣ ) T_{k}>0\left(\left|a_{k k}\right|>\sum_{j \neq k}\left|a_{k j}\right|\right) Tk>0(∣akk∣>∑j=k∣akj∣),则A总是可逆的。一旦计算出A的逆,速度v1,…,vn-1(中间点的速度)可以从 v = A − 1 c v=A^{-1}c v=A−1c计算出来,因此问题得到了解决:用(4.8)得到样条系数。
例子
另外v0=2,v6=-3。
% 三次样条:指定初始速度v0和终止速度vn,但是中间点速度未知
% Input:
% q:给定点的位置
% t:给定点位置对应的时间
% v0:初始速度
% vn:终止速度
% tt:插补周期
% Output:
% yy dyy ddyy:样条曲线函数值、速度、加速度值
function [yy dyy ddyy] = cubicSpline_2(q, t, v0, vn, tt);
if length(q) ~= length(t)
error('输入的数据应成对');
end
n = length(q);
c = zeros(n-2, 1);
% 矩阵A是个(n-2)*(n-2)的对角占优矩阵
A = zeros(n-2);
for i = 1: n-2
Tk_1 = t(i+2) - t(i+1);
Tk = t(i+1) - t(i);
if i == 1
A(i, i) = 2*(Tk + Tk_1);
A(i, i+1) = Tk;
c(i, 1) = (3/(Tk*Tk_1))*(Tk^2*(q(i+2)-q(i+1))+Tk_1^2*(q(i+1)-q(i))) - Tk_1*v0;
elseif i == n-2
A(i, i-1) = Tk_1;
A(i, i) = 2*(Tk + Tk_1);
c(i, 1) = (3/(Tk*Tk_1))*(Tk^2*(q(i+2)-q(i+1))+Tk_1^2*(q(i+1)-q(i))) - Tk*vn;
else
A(i, i-1) = Tk_1;
A(i, i) = 2*(Tk + Tk_1);
A(i, i+1) = Tk;
c(i, 1) = (3/(Tk*Tk_1))*(Tk^2*(q(i+2)-q(i+1))+Tk_1^2*(q(i+1)-q(i)));
end
end
% 经过上述步骤得到对角占优矩阵A和c
% vk = A \ c; % 这一步matlab计算很慢,应换成追赶法求vk
for i = 1: n-2
a(i) = A(i, i); % 对角线
if i == n-3
b(i) = A(i, i+1); % 上边
d(i) = A(i+1, i); % 下边
continue;
elseif i < n-2
b(i) = A(i, i+1); % 上边
d(i) = A(i+1, i); % 下边
end
end
[~, ~, vk] = crout(a, b, d, c); % 追赶法
% 得到中间插补点的速度vk,然后调用cubicSpline_1即可
v_ = [v0, vk', vn];
[yy dyy ddyy] = cubicSpline_1(q, t, v_, tt);
end
%追赶法求解三对角线性方程组,Ax=b,A用一维数组a,c,d存储。
function [L,U,x]=crout(a,c,d,b)%数组a存储三角矩阵A的主对角线元素,c、d存储主对角线上边下边带宽为1的元素
n=length(a);
n1=length(c);
n2=length(d);
%错误检查
if n1~=n2%存储矩阵的数组维数错误
error('MATLAB:Crout:不是三对角矩阵,参数数组中元素个数错误.');
elseif n~=n1+1
error('MATLAB:Crout:不是三对角矩阵,参数数组中元素个数错误.');
end
%初始化
L=zeros(n);%生成n*n的全零矩阵
U=zeros(n);
p=1:n;
q=1:n-1;
x=1:n;
y=1:n;
%追赶法程序主体
p(1)=a(1);
for i=1:n-1
q(i)=c(i)/p(i);
p(i+1)=a(i+1)-d(i)*q(i);%d的下标改为1到n-1
end
%正解y
y(1)=b(1)/p(1);%用x存储y
for i=2:n
y(i)=(b(i)-d(i-1)*y(i-1))/p(i);
end
%倒解x
x(n)=y(n);
for i=(n-1):-1:1
x(i)=y(i)-q(i)*x(i+1);
end
%L,U矩阵
for i=1:n
L(i,i)=p(i);
U(i,i)=1;
end
for i=1:n-1
L(i+1,i)=d(i);
U(i,i+1)=q(i);
end
end %end of function
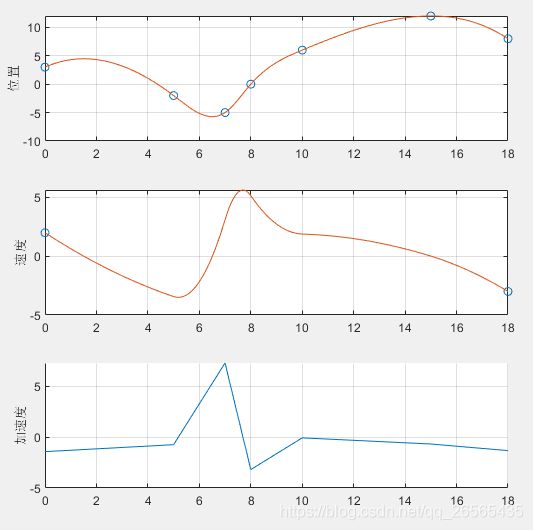
测试:
%% 自写cubicSpline_2函数测试
q = [3, -2, -5, 0, 6, 12, 8];
t = [0, 5, 7, 8, 10, 15, 18];
n = length(t);
v0 = 2; vn = -3; tt = 0.1;
[yy dyy ddyy] = cubicSpline_2(q, t, v0, vn, tt);
subplot(3, 1, 1)
plot(t, q, 'o');
ylabel('位置')
grid on
hold on
plot([t(1):tt:t(n)], yy);
subplot(3, 1, 2)
plot([t(1), t(n)], [v0, vn], 'o');
grid on
hold on
plot([t(1):tt:t(n)], dyy);
ylabel('速度')
subplot(3, 1, 3)
grid on
hold on
plot([t(1):tt:t(n)], ddyy);
ylabel('加速度')
周期三次样条:没有指定初始速度v0和最终速度vn(也就是v0和vn未知)
在许多应用中,要执行的运动是周期性的,即初始位置和最终位置相同。在这种情况下,利用为计算样条曲线而指定的最后两个自由度,以使曲线具有初始和最终速度和加速度的连续性。因此,计算系数的方法与先前报告的略有不同。事实上,在这种情况下,必须考虑代替任意选择的初始和最终速度v0和vn的条件。
最后一个公式可以写成:
![]()
代入系数表达式后,从(4.8)中得到
通过将该方程添加到系统(4.10)中,并考虑到在这种情况下,速度vn等于v0但未知(因此在(4.10)中,必须在左侧移动 T n − 2 v n T_{n-2}v_n Tn−2vn和 T 1 v 0 T_1v_0 T1v0),计算速度的线性系统变为
系统的矩阵不再是三对角的。这种情况被称为循环三对角系统,也存在有效的求解计算方法。一旦获得速度v0,…,vn−1,就可以通过(4.8)计算样条曲线的系数。
例子
% 三次样条:周期三次样条,没有指定初始速度v0和终止速度vn,也就是v0和vn未知
% Input:
% q:给定点的位置
% t:给定点位置对应的时间
% tt:插补周期
% Output:
% yy dyy ddyy:样条曲线函数值、速度、加速度值
function [yy dyy ddyy] = cubicSpline_3(q, t, tt)
if length(q) ~= length(t)
error('输入的数据应成对');
end
n = length(q);
c = zeros(n-1, 1);
% 矩阵A是个(n-1)*(n-1)的循环三对角矩阵
A = zeros(n-1);
for i = 1: n-1
if i == 1
Tn_1 = t(n) - t(n-1);
T0 = t(i+1) - t(i);
A(i, i) = 2*(Tn_1 + T0);
A(i, i+1) = Tn_1;
A(i, n-1) = T0;
c(i, 1) = (3/(Tn_1*T0))*((Tn_1^2)*(q(i+1)-q(i))+(T0^2)*(q(n)-q(n-1)));
else
Tk_1 = t(i+1) - t(i);
Tk = t(i) - t(i-1);
c(i, 1) = (3/(Tk*Tk_1))*(Tk^2*(q(i+1)-q(i))+Tk_1^2*(q(i)-q(i-1)));
if i == n-1
A(i, 1) = Tk_1;
A(i, i-1) = Tk_1;
A(i, i) = 2*(Tk + Tk_1);
else
A(i, i-1) = Tk_1;
A(i, i) = 2*(Tk + Tk_1);
A(i, i+1) = Tk;
end
end
end
% 经过上述步骤得到矩阵A和c
vk = A \ c; % 这一步matlab计算很慢,应换成追赶法求vk
% 这个vk的第一个值为v0,然后v0和vn相等
% 得到中间插补点的速度vk,然后调用cubicSpline_1即可
v_ = [vk', vk(1)];
% v_ = [-2.28 -2.78 2.99 5.14 2.15 -1.8281 -2.28]
[yy dyy ddyy] = cubicSpline_1(q, t, v_, tt);
end
测试:
%% 自写cubicSpline_3函数测试
q = [3, -2, -5, 0, 6, 12, 3];
t = [0, 5, 7, 8, 10, 15, 18];
t1 = [18, 23, 25, 26, 28, 33, 36];
n = length(t);
tt = 0.1;
[yy dyy ddyy] = cubicSpline_3(q, t, tt);
[yy_, dyy_, ddyy_] = cubicSpline_3(q, t1, tt);
subplot(3, 1, 1)
plot(t, q, 'o');
ylabel('位置')
grid on
hold on
plot([t(1):tt:t(n)], yy);
plot([t1(1):tt:t1(n)], yy_);
subplot(3, 1, 2)
% plot([t(1), t(n)], [v0, vn], 'o');
grid on
hold on
plot([t(1):tt:t(n)], dyy);
plot([t1(1):tt:t1(n)], dyy_);
ylabel('速度')
subplot(3, 1, 3)
grid on
hold on
plot([t(1):tt:t(n)], ddyy);
plot([t1(1):tt:t1(n)], ddyy_);
ylabel('加速度')
具有指定初始速度v0和最终速度vn的三次样条(v0和vn已知):基于加速度的计算
定义三次样条还有一种方法:样条曲线的一般多项式qk(t)可以表示为在其端点处计算的二阶导数的函数,也就是加速度 q ¨ ( t k ) = ω k k = 0 , . . . , n \ddot{q}\left(t_{k}\right)=\omega_{k}{k=0,...,n} q¨(tk)=ωkk=0,...,n,,而不是速度 v k v_k vk。可以计算得到此时的多项式表达式为
这样的话,速度和加速度就是如下计算式
这样的话,未知数就是加速度 ω k \omega_k ωk,因为从上面的计算式可以发现,曲线的未知参数就是加速度了,因此它是唯一定义样条曲线的。由于中间点的速度和加速度的连续性,我们得到
结合式(4.15)、(4.17)和(4.18),可以得到
其中k=1,…,n-1。另外,初始速度和最终速度有如下条件
由此可以推导得到
结合(4.19)-(4.21),可以得到如下线性系统
其中,(n+1)阶三对角对称矩阵A(其中未知参数 ω = [ ω 0 , ω 1 , . . . , ω n ] T \omega=[\omega_0,\omega_1,...,\omega_n]^T ω=[ω0,ω1,...,ωn]T)为
同样是利用追赶法解三对角线方程组,通过将解方程得到的 ω k \omega _k ωk带入(4.14)中,最终得到样条曲线。除了利用(4.14)来描述三次样条曲线之外,显然,还是可以根据初始定义来描述三次样条曲线,即
其中样条曲线的参数a呢就可以通过已知的点 q k q_k qk和已经求得的加速度 ω k \omega _k ωk来计算,计算式如下
这个方法主要是为下面的方法做准备,因此不写例子。
具有指定初始、最终速度以及加速度的三次样条曲线
样条曲线是一个二阶连续导数的函数,但通常不可能同时指定初始速度和最终速度以及加速度。因此,样条曲线在其末端的特征是速度或加速度的不连续性,一般情况下我们会指定初始和最终速度,则此时初始和最终加速度难以保证连续,会出现突变。下面需要做的就是需要保证在指定初始速度和最终速度的前提下,还要保证初始、最终加速度从0开始连续变化。如果这些不连续代表一个问题,可以采用不同的方法:
-
一个5次多项式函数可以用于第一个和最后一个域,其缺点是允许在这些段中有更大的超调,并且稍微增加了计算负担;
-
在第一段和最后一段中添加两个自由额外点(从这个意义上说,这些点不能先验地固定),并通过施加所需的速度和加速度的初始值和最终值来计算它们的值。
后一种方法现在详细说明。让我们考虑一个要插值的n-1点向量,这两个向量中都没有第二个值以及倒数第二个值,也就是q1、t1和qn-1、tn-1(目前我还不知道为啥要这么做。。。)
对应的时间节点为
以及同时考虑速度v0,vn和加速度a0,an的边界条件。为了施加所需的加速度,增加了两个额外的点 q ˉ 1 \bar{q}_{1} qˉ1 和 q ˉ n − 1 \bar{q}_{n-1} qˉn−1。时间瞬间 t 1 ‾ \overline{t_{1}} t1 和 t ˉ n − 1 \bar{t}_{n-1} tˉn−1分别位于t0和t2之间以及tn-2和tn之间。不过可以分析得到,这种处理办法虽然能够对一条轨迹施加轨迹长度、初始速度、终止速度、初始加速度、终止加速度这五种约束条件,但是前提是额外增加两个轨迹点以及时间点,这样可能破坏时间最优规划的初衷,额外增加约束可能也会导致轨迹灵活性变差。。。
增加的这两个点,可以通过已知的变量去表达这两个点,即初始/最终的位置、速度以及加速度(q0/qn,v0/vn,a0/an)同时包括在这些点上的加速度w1和wn-1(其中边界点的加速度是用a0和an来表示,而中间点的加速度是用w来表示)。这样,就可以考虑初始加速度和最终加速度的约束。
将(4.26)和(4.27)替换掉(4.24)中的有关项,通过重新排列n-1方程,我们得到一个线性系统
其中
注意,T0、T1和Tn-2、Tn-1分别是 t 1 ‾ \overline{t_{1}} t1 和 t ˉ n − 1 \bar{t}_{n-1} tˉn−1的函数,可以在间隔(t0、t2)和(tn-2、tn)中任意选择,例如
通过求解方程组(4.28)可以得到中间插补点的加速度为
与边界值a0和an一起,就可以根据(4.14)或者(4.25)计算整体的样条曲线。
例子
其中v0=2,vn=-3,a0=0,an=0。额外增加的两个时间点t1=2.5,t7=16.5,当然也可以任意选择。
% 三次样条:指定初始、终止速度以及加速度,也就是v0,vn,a0,an已知
% 这个方法需要增加两个额外的点q1_和qn-1_
% q1_在原有q1和q2之间,qn-1_在原有的qn-1和qn之间
% 这两个额外点对应的时间t1_和tn-1_需要计算,可以任意选择,本程序选择取平均值
% Input:
% q:给定点的位置
% t:给定点位置对应的时间
% v0:初始速度
% vn:终止速度
% a0:初始加速度
% an:终止加速度
% tt:插补周期
% Output:
% yy dyy ddyy:样条曲线函数值、速度、加速度值
function [yy dyy ddyy q1 qn_1] = cubicSpline_4(q, t, v0, vn, a0, an, tt)
if length(q) ~= length(t)
error('输入的数据应成对');
end
n = length(q); % 原来的点数量
% 增加两个额外点q1_和qn-1_,计算两点对应的时间点
t1_ = (t(1)+t(2)) / 2;
tn_1_ = (t(n-1)+t(n)) / 2;
% 更新时间向量
t = [t(1), t1_, t(2: n-1), tn_1_, t(n)];
% 更新点的数量
n = n + 2;
% 矩阵A是个(n-2)阶对角占优矩阵
A = zeros(n-2);
c = zeros(n-2, 1);
for i = 1: n-2
Tk_1 = t(i+2) - t(i+1);
Tk = t(i+1) - t(i);
if i == 1
A(i, i) = 2*Tk_1 + Tk*(3+Tk/Tk_1);
A(i, i+1) = Tk_1;
c(i, 1) = 6*((q(2)-q(1))/Tk_1-v0*(1+Tk/Tk_1)-a0*(0.5+Tk/(3*Tk_1))*Tk);
elseif i == 2
T0 = t(2)-t(1);
A(i, i-1) = Tk - (T0^2)/Tk;
A(i, i) = 2*(Tk + Tk_1);
A(i, i+1) = Tk_1;
c(i, 1) = 6*((q(3)-q(2))/Tk_1-(q(2)-q(1))/Tk+v0*(T0/Tk)+a0*(T0^2)/(3*Tk));
elseif i == n-2-1
Tn_1 = t(n) - t(n-1);
A(i, i-1) = Tk;
A(i, i) = 2*(Tk + Tk_1);
A(i, i+1) = Tk_1 - (Tn_1^2)/Tk_1;
c(i, 1) = 6*((q(n-2)-q(n-3))/Tk_1-(q(n-3)-q(n-4))/Tk-vn*(Tn_1/Tk_1)+an*(Tn_1^2)/(3*Tk_1));
elseif i == n-2
A(i, i) = 2*Tk + Tk_1*(3+Tk_1/Tk);
A(i, i-1) = Tk;
c(i, 1) = 6*((q(n-3)-q(n-2))/Tk+vn*(1+Tk_1/Tk)-an*(0.5+Tk_1/(3*Tk))*Tk_1);
else
A(i, i-1) = Tk;
A(i, i) = 2*(Tk + Tk_1);
A(i, i+1) = Tk_1;
c(i, 1) = 6*((q(i+1)-q(i))/Tk_1-(q(i)-q(i-1))/Tk);
end
end
% 经过上述步骤得到对角占优矩阵A和c
wk = A \ c; % 这一步matlab计算很慢,应换成追赶法求vk
% for i = 1: n-2
% a(i) = A(i, i); % 对角线
% if i == n-3
% b(i) = A(i, i+1); % 上边
% d(i) = A(i+1, i); % 下边
% continue;
% elseif i < n-2
% b(i) = A(i, i+1); % 上边
% d(i) = A(i+1, i); % 下边
% end
% end
% [~, ~, wk_] = crout(a, b, d, c); % 追赶法
n_ = length(wk);
q1 = q(1) + T0*v0 + ((T0^2)/3)*a0 + ((T0^2)/6)*wk(1);
Tn_1 = t(n) - t(n-1);
qn_1 = q(n-2) - Tn_1*vn + ((Tn_1^2)/3)*an + ((Tn_1^2)/6)*wk(n_);
% 更新位置q向量
q = [q(1), q1, q(2: n-3), qn_1, q(n-2)];
% 更新加速度w向量
w = [a0, wk', an];
% 规划样条轨迹
T = t(n) - t(1); % 运行总时长
nn = T / tt; % 总点数
yy = zeros(1, nn);
dyy = zeros(1, nn);
ddyy = zeros(1, nn);
j = 1;
for i = 1: n-1
Tk = t(i+1) - t(i);
a0 = q(i);
a1 = (q(i+1)-q(i))/Tk-(Tk/6)*(w(i+1)+2*w(i));
a2 = w(i) / 2;
a3 = (w(i+1)-w(i))/(6*Tk);
for tk = t(i): tt: t(i+1)
if i > 1 && tk == t(i)
continue
end
yy(j) = a0 + a1*(tk-t(i)) + a2*power(tk-t(i), 2) + a3*power(tk-t(i), 3);
dyy(j) = a1 + 2*a2*(tk-t(i)) + 3*a3*power(tk-t(i), 2);
ddyy(j) = 2*a2 + 6*a3*(tk-t(i));
j = j + 1;
end
end
end
测试:
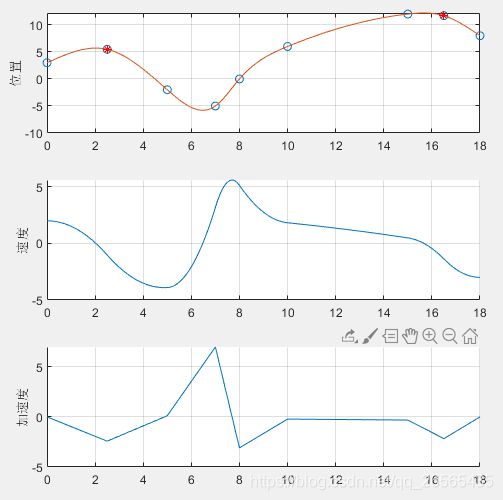
%% 自写cubicSpline_4函数测试
q = [3, -2, -5, 0, 6, 12, 8];
t = [0, 5, 7, 8, 10, 15, 18];
v0 = 2; vn = -3; a0 = 0; an = 0;
tt = 0.1;
n = length(t);
[yy dyy ddyy q1 qn_1] = cubicSpline_4(q, t, v0, vn, a0, an, tt);
% 增加两个额外点q1_和qn-1_,计算两点对应的时间点
t1_ = (t(1)+t(2)) / 2;
tn_1_ = (t(n-1)+t(n)) / 2;
% 更新时间向量
t = [t(1), t1_, t(2: n-1), tn_1_, t(n)];
n = length(t);% 更新n
% 更新q
q = [q(1), q1, q(2: n-3), qn_1, q(n-2)];
subplot(3, 1, 1)
plot(t, q, 'o');
ylabel('位置')
grid on
hold on
plot([t(1):tt:t(n)], yy);
hold on
plot(t(2), q(2), 'r*');
plot(t(n-1), q(n-1), 'r*');
subplot(3, 1, 2)
% plot([t(1), t(n)], [v0, vn], 'o');
grid on
hold on
plot([t(1):tt:t(n)], dyy);
ylabel('速度')
subplot(3, 1, 3)
grid on
hold on
plot([t(1):tt:t(n)], ddyy);
ylabel('加速度')
三次样条部分还有平滑三次样条,后面再写,今天就到这里~
参考文献(实际上我就是翻译了一下下。。。)
Trajectory Planning for Automatic Machines and Robots