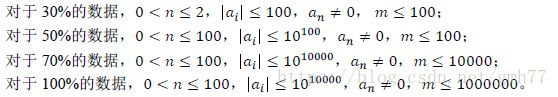jzoj3935. 【NOIP2014day2官方数据】解方程

问题描述

70%

因为数字太大搞不了，所以考虑处理每个数取模后的值
每次枚举x，判断x是否在模意义下成立

当然这样做无法保证正确性，所以考虑用多模数来做
70%的话只需要取998244353和1000000007就够了
时间复杂度：$O(Tnm)$ （T是模数个数）

80%

把原多项式变成递推，每次找到一个xi后就用原多项式去除(x-xi)
这样可以水到80分当然加个O3说不定更高

100%

显然x在模p意义下是，x和x+kp的值相同
所以对于每个模数，只需要枚举0~p-1就可以知道剩下的结果了

如果一个数在所有模数意义下都为0，那么这个数就可能是答案
为了保证正确性，同时为了避免longlong和减小时间复杂度，10个4万左右的模数就够了
具体可以看标

code

#include 
#include 
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define N 10
using namespace std;

int hash[N+1]={0,40009,40013,40031,40037,40039,40063,40087,40093,40099,40111};
int a[N+1][101];
int n,m,i,j,k,l,tot,x,sum;
int bz[1000001];
char ch;
bool Bz;

int main()
{
	scanf("%d%d\n",&n,&m);
	fo(i,0,n)
	{
		ch=getchar();
		if (ch=='-')
		Bz=1;
		else
		{
			Bz=0;
			fo(j,1,N)
			a[j][i]=ch-'0';
		}
		
		ch=getchar();
		while (ch!='\n')
		{
			fo(j,1,N)
			a[j][i]=(a[j][i]*10+(ch-'0'))%hash[j];
			
			ch=getchar();
		}
		
		if (Bz)
		{
			fo(j,1,N)
			a[j][i]=(hash[j]-a[j][i])%hash[j];
		}
	}
	
	fo(j,1,N)
	{
		fo(x,0,hash[j]-1)
		{
			sum=0;
			fd(i,n,0)
			sum=(sum*x+a[j][i])%hash[j];
			
			if (!sum)
			{
				k=x;
				while (k<=m)
				{
					bz[k]++;
					k+=hash[j];
				}
			}
		}
	}
	
	fo(i,1,m)
	if (bz[i]==N)
	tot++;
	printf("%d\n",tot);
	
	fo(i,1,m)
	if (bz[i]==N)
	printf("%d\n",i);
	
	return 0;
}