整数（奇偶）+分数分频器的verilog实现（大合集）

分频在数字设计中应用广泛，通常可以使用锁相环PLL和计数器实现。本文介绍的分频器是基于计数器实现的，由于使用的是DFF（D触发器），这实际上是行波计数器（一串DFF级联，上级的输出作为下级的时钟）的推广，在同步实现中，一般不使用这种分频后的波形（因为DFF的Tco会逐级积累，使得分频前后的时钟不是100%同步，若将DFF的输出信号作为其他DFF的时钟，第一，极限情况容易违反Tsu和Thold，进而产生亚稳态；第二，这为STA和插入扫描链增加了难度）。但是，作为一种分频的思想，还是有讨论的价值的，或者说，在低频电路中，使用起来也不会对电路造成太大问题（不要多级级联，即不要将得到的时钟信号在进行分频作为其他模块的时钟）。

NOTE：扫描链（Scan chain）是可测试性设计的一种实现技术。它通过植入移位寄存器，使得测试人员可以从外部控制和观测电路内部触发器的信号值。

---

一、50%占空比整数分频

这是计数器分频中最简单最基础的分频方式。一般可分为奇数分频和偶数分频。

1.1 奇数分频器

1.1.1 方法1：2N分频上下沿波形相异或

生成2N分频的上升沿和下降沿触发的波形，二者异或可得到N奇数分频波形。

具体方法：N为奇数

Step1：生成标志信号

上升沿波形翻转标志信号：

tff1_en = (clk_cnt == 0);

下升沿波形翻转标志信号：

tff2_en = (clk_cnt == (N + 1) / 2);

Step2：在DFF中翻转（div1、div2位2N个clk，计数到2N-1清零）

always @ (posedge clk) If (tff1_en) Div1 <= ~div1;

always @ (negedge clk) If (tff2_en) Div2 <= ~div2;

Step3：异或得到N奇分频波形

assign div_odd = div1 ^ div2;

1.1.2 方法2：N分频上下沿波形相或（输出初始态为0）

在N分频波形内进行操作。

具体操作：

Step1：产生上升/下降沿波形翻转标志

tff1_en = (clk_cntp == (N – 1) / 2 | clk_cntp == N – 1); // clk_cntp为上升沿计数器

tff2_en = (clk_cntn == (N – 1) / 2 | clk_cntn == N – 1); // clk_cntn 为下降沿计数器

Step2：（div1、2为N个clk，计数到N-1清零）

always @ (posedge clk) if (Tff1_en) div1 <= ~div1;

always @ (negedge clk) if (Tff2_en) div2 <= ~div2;

Step3：div1与div2相或（初始态为0）、相与（初始态为1）

assign div_odd = (div1 | div2); / Div_odd = (div1 & div2);

推荐采用方法1。

---

1.2 偶数分频器

N为偶数，如下操作：

Step1：计数值一半时，产生翻转标志

tff_en=clk_cnt==N/2-1;

Step2：取反，div包含了N个clk，到N/2-1清零计数器；

always @ (posedge clk) if (tff_en) div <= ~div;

Step3：输出

assign div_even = div;

NOTE：因为偶数分频，分频后的时钟总是高低电平一半，所以按如下方式：计数器计数到N-1清零，翻转的tff_en = (clk_cnt == N/2-1) || (clk_cnt == N-1);

---

二、非50%占空比分频

假设给定：占空比DUTY（范围0-100，精度1），分频系数N；

算法：因为是任意占空比，所以不考虑奇偶分频的差异；

Step1：even_flag == N[0]; // 根据N最低位判定是偶分频还是奇分频

Step2：计算第一个翻转值clk_cnt == N*DUTY/100;

Step3：tff_en = clk_cnt == N*DUTY/100 || clk_cnt == N-1;

目标是得到一定占空比的波形，所以不需要100%的精确控制，上述算法具有缺陷，即N和DUTY不能同时太小，否则因为除法的整除原则，会舍弃掉一部分信息，而造成结果的不正确。故，一般的简单分频要求的场合可以按照上述方式实现。特殊情况，需要使用PLL等来生成高精度高要求的目标时钟。

---

三、小数（分数）分频

小数（分数）分频也算是老生常谈的话题。其中，常见的类型是产生N+0.5分频，即0.5倍分频。

3.1 N+0.5分频

原理：N+0.5，占空比为（N+1）/（2N+1）

Step1：上升/下降沿计数器清零

always @ (posedge clk) if (clk_cntp == 2N) clk_cntp <= 0;

always @ (negedge clk) if (clk_cntn == 2N) clk_cntn <= 0;

step2：产生翻转标志

assign tff_en1 = (clk_cntp == N+1 | 0);

assign tff_en2 = (clk_cntn == N+1 | 1);

step3：波形翻转

always @ (posedge clk) if (tff_en1) div1 <= ~div1; // 初始态为0

always @ (negedge clk) if (tff_en2) div2 <= ~div2; // 初始态与div1相反

step4：两者相与

assign div = div & div2;

---

3.2 任意小数分频

3.2.1 基于脉冲删除小数分频的算法描述

本节讨论的小数分频方案属于前置双模小数分频器，顾名思义，即包含两个整数分频器，如下图3-2.1，是双模分频器的典型结构框图。

要实现小数x分频，记x=nume/deno（不考虑舍去，如3.7分频可以表示为37/10分频，分母deno=10，分子nume=37），则：

M = nume / deno，remd = nume % deno，
remd * (M+1) + (deno-remd) * M = remd + deno * M = nume

即分子=余数+商*分母。则在deno个输出波形中包含了nume个参考时钟，实现了对参考时钟的nume/deno分频（输出由remd个M+1分频时钟和deno-remd个M分频时钟组成）。

图3-2.1 典型双模小数分频结构示意图

得到上述M和M+1分频时钟后，需要将两者平均分配，这就需要一个控制电路，输出的组合有多种，需要选择一种较好的分配组合方案，以得到没有太大抖动的时钟（时钟频率均匀性好，相位抖动会减小）。有关分配方案的选择，参考以下文章时钟分频系列——偶数分频/奇数分频/分数分频，文中对不同情况进行了分析最后选出最优方案。但，文中的方案需要作M+1和M的控制算法，比较复杂，始终感觉有点多余。且，这种控制逻辑很有可能在输出产生毛刺。如下图3-2.2是文中小数分频的结构视图。

图3-2.2 基于ACCT计数器的小数分频实现原理图

本文采用的方案与上述不同。方案如下：

目的是实现nume个参考时钟内，输出deno个有M和M+1分频的时钟。实际上，就是在原有nume个参考时钟中，选择性地输出deno个脉冲（只不过输出的脉冲宽度可能与参考不一样），所以只需要在nume个脉冲中删除nume-deno个脉冲，那么输出就含有了deno个脉冲，就达到nume/deno分频的目的。

算法实现：
// ----------------------------------------算法实现描述---------------------------------------- //
算法框图如下图3-2.3所示，算法模型实际是一个计数器，采用计数器来实现除法操作。P为分子，Q为分母，记P/Q=M…remd（商为M，余数remd）初始化后每次clk_cnt+Q后与P比较，实际上是计算P/Q的个数，即加多少次Q能加到P，因为初始值的不同，所以出现的情况有两种，M和M+1次（[M=P/Q]取整）。若加M次加法后都小于P，则表示还可以包含1个clk_ref，则输出的是M+1分频，1表示之前做了M次加法，前M次都输出1，最后1次输出clk_ref（之前clk_cnt加上Q还在P范围之内）；若做了M-1次加法后再做1次就超出P，说明P中只包含M-1个Q，前M-1次均输出1，最后1次输出clk_ref，总共为M+0；当某一次clk_cnt+Q==P时，即余数为0，1次完成的分频波形输出成功（M+1分频remd次，M分频Q-remd次）。按照以上描述循环判断并输出，就可以得到remd个M+1分频和Q-remd个M分频的平均组合输出。
// ------------------------------------------------------------------------------------------------- //

but，为什么就是M+1和M的平均组合输出呢？

这个问题，需要思考一下。因为余数为remd，实际上就是控制了M+1分频的个数，Q-remd就是控制循环的结束（一个完整循环）。每作M或M-1次加Q操作后都会产生1个计算余数（不同于上述remd），该计算余数作为下一次分频的起始计数值，每次增加Q，则计算余数会按照算数规律周期地平均分配M和M+1分频时钟，最终，计算余数完成循环归0。这里，不得不感慨算术的美学，这样一个简单的加法，却能够实现如此复杂的算法控制。

图3-2.3 脉冲删除小数分频实现的算法流程图

---

3.2.2 脉冲删除小数分频的仿真

为了直观地展示上述算法，举例说明，和上文图3-2.2中一样，实现8.7分频。仿真波形图如下图3-2.4，看出，clk_out按照 9998-998-998 的这方式，且输出没有毛刺，与基于ACCT方式实现的方案一致。

图3-2.4 脉冲删除小数分频实现8.7分频仿真波形

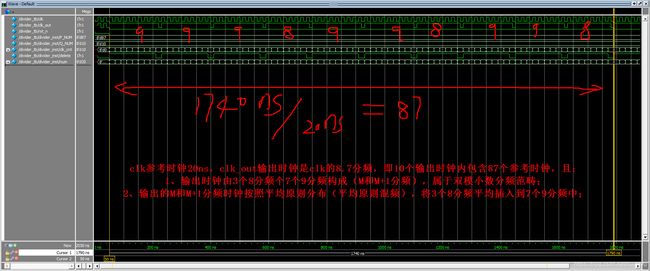
实际上，ACCT实现8.7分频，文中给出了3中输出组合，文中作者最终选择的方案与本文仿真结果的方案一致。如下图3-2.5，是8.7分频的输出组合方案。文章中作者需要判定哪种组合的输出抖动小，然后在verilog代码中修改case项，实现不同的混频输出，而，本文基于加法计数器的算数逻辑，巧妙避免人为的方案选择，算法会自动选择最优解输出分频波形。

图3-2.5 小数8.7分频输出组合方案

---

3.2.3 脉冲删除小数分频的RTL代码

RTL代码如下：

module clk_divider # (
	parameter P_NUM = 8'd13 ,
	parameter Q_NUM = 8'd11 ,
	parameter CNT_WID = 8

) (
	input 	clk ,
	input 	rst_n ,
	
	output  clk_out
);

reg delete;
wire [CNT_WID - 1 : 0] num;
reg  [CNT_WID - 1 : 0] clk_cnt;
assign num = clk_cnt + Q_NUM; // 测试用，观察clk_cnt+ Q_NUM的值

always @ (posedge clk) begin
	if (!rst_n)
		delete <= 1'b0;
	else if (clk_cnt + Q_NUM >= P_NUM)
		delete <= 1'b0;
	else if (clk_cnt + Q_NUM < P_NUM ) 
		delete <= 1'b1;
end

always @ (posedge clk) begin
	if (!rst_n)
		clk_cnt <= {CNT_WID{1'b0}};
	else begin
		if (clk_cnt + Q_NUM >= P_NUM)
			clk_cnt <= clk_cnt + Q_NUM - P_NUM;
		else 
			clk_cnt <= clk_cnt + Q_NUM;
	end	
end

assign clk_out = (delete) ? 1'b1 : clk;

endmodule