题目链接
P3388 【模板】割点(割顶)
解题思路
最近学的东西太杂了,多写点博客免得自己糊里糊涂的过去了。
这个题求割点,感觉这篇文章写得挺好。
割点是啥?如果去掉这个点之后连通图变成多个不连通图了,那这个点就是割点。
那我们如何求割点呢?显然,我们可以无视复杂度枚举一下每个点然后\(DFS\)一下看看图连不连通。
那我们能不能在更好的复杂度下求割点呢?可以。
首先,深搜一下这个连通图,标记一下深度(\(dep\),或者大部分博客里写的\(DFS\)序\(dfn\),但我觉得深度更易理解)。
void dfs(int p,int f){//p是当前节点,f是dfs树中p的父亲节点
int q,i;
dep[p]=dep[f]+1;
for(i=head[p];i;i=e[i].near){
q=e[i].end;
if(!dep[q])//这句话保证了进入dfs的点必然是没访问过的
dfs(q,p);
}
}然后呢,我们观察一下这个\(dfs\)树的性质。
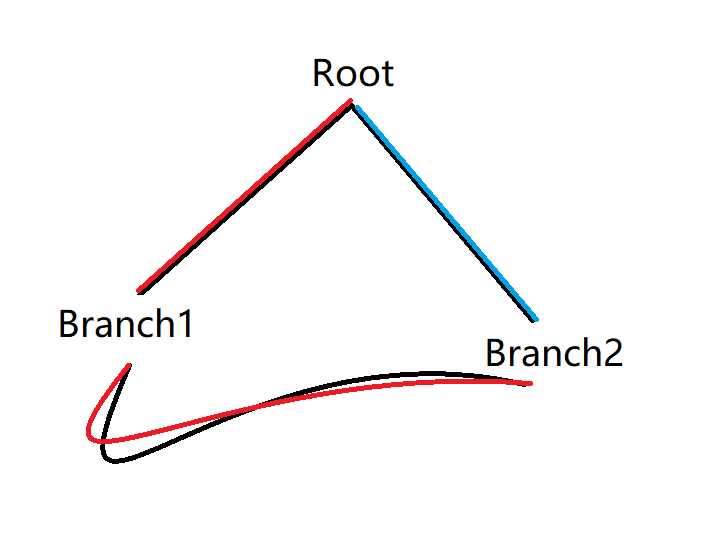
首先,这个树的根节点只要伸出去多个枝(\(\geq 1\)),那么它就是一个割点。
因为这两个(或多个)枝条之间只要有连接,那么必定在\(dfs\)树中只会以一个枝条的形式出现。
如下图,红色代表能够走的边,蓝色因为根节点已经访问过了而无法继续走。
于是我们有了这个\(DFS\)的代码:
void dfs(int p,int f){
int q,i,child=0;
dep[p]=dep[f]+1;
for(i=head[p];i;i=e[i].near){
q=e[i].end;
if(!dep[q]){
dfs(q,p);
if(!f)child++;
}
}
if(!f&&child>1)cut[p]=1,num++;//只要有多个孩子就是割点
}别急,还有非根节点没有解决呢。
其实与根节点同理,非根节点如果有两个以上的互相不能联通的枝条的话,那它就是一个割点了。
那么怎么判断它的两个枝条连通与否呢?很简单,只要看它有没有枝条不能走到它祖先位置上即可。
也就是说,把一个点的子树看成\(Branch1\),把其祖先那一串东西看成\(Branch2\),如果这俩东西不能连通那么这个点就是割点啦。
于是引入新的数组\(low\),保存的内容是其能够到达的\(dep\)最小的\(dep\)值(即最浅深度)。
然后新鲜出炉的DFS长这样:
void dfs(int p,int f){
int q,i,child=0;
dep[p]=low[p]=dep[f]+1;//最小的深度先设为自己的深度
for(i=head[p];i;i=e[i].near){
q=e[i].end;
if(!dep[q]){
dfs(q,p);
if(low[q]=dep[p]&&f&&!cut[p])cut[p]=1,num++;
if(!f)child++;
}
if(dep[q]1)cut[p]=1,num++;
} 代码中注释出的重点,为什么不能写成\(low[p]=min(low[p],low[q])\)呢?
其实是因为,如果已经在某个节点遍历到一根返祖边,那么这个节点的\(low\)值由此会变成孩子节点的\(low\)即祖先节点的\(dep\)值,再对其其他孩子进行遍历的时候,会有可能将孩子节点的\(low\)值更新为该节点的\(low\)即祖先的\(dep\)值,而将本该是割点的点忽略掉。
如果不理解,试试\(debug\)一下这组数据:
6 7
1 2
2 3
3 4
2 4
2 5
5 6
1 6
AC代码
#include
int num,head[20010],cnt,low[20010],dep[20010],cut[20010],n,m;
struct Edge{
int end,near;
}e[200002];
void add(int a,int b){
e[++cnt].end=b;e[cnt].near=head[a];head[a]=cnt;
}
void dfs(int p,int f){
int q,i,child=0;
dep[p]=low[p]=dep[f]+1;
for(i=head[p];i;i=e[i].near){
q=e[i].end;
if(!dep[q]){
dfs(q,p);
if(low[q]=dep[p]&&f&&!cut[p])cut[p]=1,num++;
if(!f)child++;
}
if(dep[q]1)cut[p]=1,num++;
}
int main(){
int i,u,v;
scanf("%d%d",&n,&m);
for(i=0;i