Huffman 算法原理及代码实现
Huffman 算法原理
前缀码
在一个字符集中,任何一个字符的编码都不是另一个字符编码的前缀,即前缀码。 例如,有两个码字 111 与 1111,那么这两个码字就不符合前缀码的规则,因为 111 是
1111 的前缀。放到二叉树里来讲,只用叶子节点编码的码字才是前缀码,如果同时使用 中间节点和叶子节点编码,那结果就不是前缀码。因为压缩中经过编码的码字全部是前 缀码,所以在对照码表解压的时候,碰到哪个码字就是哪个码字,不用担心出现某个字 符的编码是另一个字符的编码的前缀的情况,该意识一定要具备。
关于前缀码,下面一段话摘自《算法导论》:“前缀码的作用是简化解码过程。由于 没有码字是其他码字的前缀,编码文件的开始码字是无歧义的。我们可以简单的识别出 开始码字,将其转换会原字符,然后对编码文件剩余部分重复这种解码过程。
1111111 ? 111 1111 ? 1111 111
哈夫曼编码
哈夫曼设计了一个贪心算法来构造最优前缀码,被称为哈夫曼编码(Huffman code), 其正确性证明依赖于贪心选择性质和最优子结构。哈夫曼编码可以很有效的压缩数据,
具体压缩率依赖于数据本身的特性。这里我们先介绍几个概念:码字、码字长度、定长 编码与变长编码。
每个字符可以用一个唯一的二进制串表示,这个二进制串称为这个字符的码字,这 个二进制串的长度称为这个码字的码字长度。码字长度固定就是定长编码,码字长度不 同则为变长编码。变长编码可以达到比定长编码好得多的压缩率,其思想是赋予高频字 符(出现频率高的字符)短(码字长度较短)码字,赋予低频字符长码字。例如,我们 用 ASCII 字符编辑一个文本文档,不论字符在整个文档中出现的频率,每个字符都要占 用一个字节;如果我们使用变长编码的方式,每个字符因在整个文档中的出现频率不同 导致码字长度不同,有的可能占用一个字节,而有的可能只占用一比特,这个时候,整 个文档占用空间就会比较小了。当然,如果这个文本文档相当大,导致每个字符的出现 频率基本相同,那么此时所谓变长编码在压缩方面的优势就基本不存在了(这点要十分 明确,这是为什么压缩要分块的原因之一,后续源码分析会详细讲解)。
哈夫曼编码会自底向上构造出一棵对应最优编码的二叉树,我们使用下面这个例子 来说明哈夫曼树的构造过程。首先,我们已知在某个文本中有如下字符及其出现频率,
| 字符 |
a |
b |
c |
d |
e |
f |
| 出现频率 |
45 |
13 |
12 |
16 |
9 |
5 |
构造过程如下图所示:
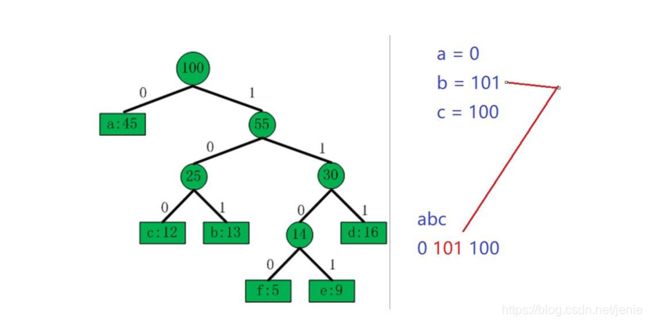
图 1 到图 6 列除了整个哈夫曼树构造过程中的每个步骤。在一开始,每个字符都已 经按照出现频率大小排好顺序,在后续的步骤中,每次都将频率最低的两棵树合并,然 后用合并后的结果再次排序(注意,排序不是目的,目的是找到这时出现频率最低的两 项,以便下次合并。gzip 源码中并没有专门去“排序”,而是使用专门的数据结构把频率 最低的两项找到即可)。叶子节点用矩形表示,每个叶子节点包含一个字符及其频率。中 间节点用圆圈表示,包含其孩子节点的频率之和。中间节点指向左孩子的边标记为 0, 指向右孩子的边标记为 1。一个字符的码字对应从根到其叶节点的路径上的边的标签序 列。图 1 为初始集合,有六个节点,每个节点对应一个字符;图 2 到图 5 为中间步骤,
图 6 为最终哈夫曼树。此时每个字符的编码都是前缀码。
哈夫曼压缩和解压文件
利用库中的优先级队列实现哈夫曼树,最后基于哈夫曼树最终实现文件压缩。
1.统计文件中字符出现的次数,利用优先级队列构建 Haffman 树,生成 Huffman 编 码。构造过程可以使用 priority_queue 辅助,每次 pq.top()都可以取出权值(频数)最小 的节点。每取出两个最小权值的节点,就 new 出一个新的节点,左右孩子分别指向它 们。然后把这个新节点 push 进优先队列。
2.压缩:利用 Haffman 编码对文件进行压缩,即在压缩文件中按顺序存入每个字符 的 Haffman 编码。 码表(实际存储是对应数值的概率,然后调用程序生成码表) + 编码
3.将文件中出现的字符以及它们出现的次数写入配置文件中,以便后续压缩使用。
4.解压缩:利用配置文件重构 Haffman 树,对文件进行减压缩。
HuffmanTree.hpp
#ifndef _HUFFMAN_TREE_H_
#define _HUFFMAN_TREE_H_
#include
#include
#include
#include
using namespace std;
template
struct HuffmanTreeNode
{
HuffmanTreeNode(const W &weight)
: _pLeft(NULL)
, _pRight(NULL)
, _pParent(NULL)
, _weight(weight)
{}
HuffmanTreeNode*_pLeft;
HuffmanTreeNode*_pRight;
HuffmanTreeNode*_pParent;
W _weight;
};
template
class HuffmanTree
{
typedef HuffmanTreeNode*PNode;
public:
HuffmanTree()
: _pRoot(NULL)
{}
HuffmanTree(W*array, size_t size, const W&invalid)
{
_CreateHuffmantree(array, size, invalid);
}
void _Destroy(PNode&pRoot)
{
//后序
if (pRoot)
{
_Destroy(pRoot->_pLeft);
_Destroy(pRoot->_pRight);
delete pRoot;
pRoot = NULL;
}
}
~HuffmanTree()
{
_Destroy(_pRoot);
}
PNode GetRoot()
{
return _pRoot;
}
private:
//构建哈夫曼树
void _CreateHuffmantree(W*array, size_t size, const W&invalid)
{
struct PtrNodeCompare
{
bool operator()(PNode n1, PNode n2)//重载“()”
{
return n1->_weight < n2->_weight;
}
};
priority_queue, PtrNodeCompare>hp; // 最大堆
for (size_t i = 0; i < size; ++i)
{
if (array[i] != invalid)
{
hp.push(new HuffmanTreeNode(array[i])); // 数据入堆
}
}
//空堆
if (hp.empty())
_pRoot = NULL;
while (hp.size()>1)
{
PNode pLeft = hp.top();
hp.pop();
PNode pRight = hp.top();
hp.pop();
PNode pParent = new HuffmanTreeNode(pLeft->_weight + pRight->_weight);//左加右的权值,作为新节点
pParent->_pLeft = pLeft;
pLeft->_pParent = pParent;
pParent->_pRight = pRight;
pRight->_pParent = pParent;
hp.push(pParent);
}
_pRoot = hp.top(); // 节点在堆
}
public:
PNode _pRoot;
};
#endif FileCompress.hpp
/*利用库中的优先级队列实现哈夫曼树,最后基于哈夫曼树最终实现文件压缩。
描述:
1.统计文件中字符出现的次数,利用优先级队列构建Haffman树,生成Huffman编码。
构造过程可以使用priority_queue辅助,每次pq.top()都可以取出权值(频数)最小的节点。每取出两个最小权值的节点,就new出一个新的节点,左右孩子分别指向它们。然后把这个新节点push进优先队列。
2.压缩:利用Haffman编码对文件进行压缩,即在压缩文件中按顺序存入每个字符的Haffman编码。
3.将文件中出现的字符以及它们出现的次数写入配置文件中,以便后续压缩使用。
4.解压缩:利用配置文件重构Haffman树,对文件进行减压缩。
*/
#ifndef _FILE_COMPRESS_H_
#define _FILE_COMPRESS_H_
#include "HuffmanTree.hpp"
#include
#include
#include
#include
using namespace std;
unsigned long getFileSize(const char *path)
{
unsigned long filesize = -1;
FILE *fp;
fp = fopen(path, "r");
if(fp == NULL)
return filesize;
fseek(fp, 0L, SEEK_END);
filesize = ftell(fp);
fclose(fp);
return filesize;
}
typedef unsigned int CountType;
typedef unsigned char CharType;
struct CharInfo
{
CharType _ch;//字符
CountType _count;//次数
string _code;//编码
bool operator!=(const CharInfo &info)
{
return _count != info._count;
}
CharInfo operator+(const CharInfo &info)
{
CharInfo ret;
ret._count = _count + info._count;
return ret;
}
bool operator<(const CharInfo &info)
{
return _count > info._count;
}
};
class FileCompress
{
typedef HuffmanTreeNode Node;
struct TmpInfo
{
CharType _ch;//字符
CountType _count;//次数
};
public:
//构造函数
FileCompress()
{
for (size_t i = 0; i < 256; ++i)
{
_infos[i]._ch = i;
_infos[i]._count = 0;
}
}
//获取哈夫曼编码
void GenerateHuffmanCode(Node *root, string code)
{
if (root == NULL)
return;
//前序遍历生成编码
if (root->_pLeft == NULL && root->_pRight == NULL)
{
_infos[(unsigned char)root->_weight._ch]._code = code;
return;
}
GenerateHuffmanCode(root->_pLeft, code + '0');
GenerateHuffmanCode(root->_pRight, code + '1');
}
// 真正的压缩算法窗口是32k, 我们这里直接对所有数据进行编码
void Compress(const char *file) //file:源文件
{
unsigned long fileSize = getFileSize(file);
//1.统计字符出现的次数
FILE *fout = fopen(file, "rb");
assert(fout);
char ch = fgetc(fout);
while (feof(fout) == 0) //如文件结束,则返回值为1,否则为0
{
_infos[(unsigned char)ch]._count++; // 计算对应字符出现的频率
ch = fgetc(fout);
}
//2.生成Huffmantree 及code
CharInfo invalid;
invalid._count = 0;
// 2.1 生成Huffmantree, 构建哈夫曼树
HuffmanTree tree(_infos, 256, invalid); //参数:数组,256个,无效值(出现0次)
string compressfile = file; //
compressfile += ".huffman"; //?
FILE *fin = fopen(compressfile.c_str(), "wb"); //打开压缩文件
assert(fin);
string code;
// 2.2 生成code
GenerateHuffmanCode(tree.GetRoot(), code);
//3.0 写入字符出现的信息
int writeNum = 0;
int objSize = sizeof(TmpInfo);
for (size_t i = 0; i < 256; ++i) // 这里实质是讲码表存储到文件的头部
{
if (_infos[i]._count > 0)
{
TmpInfo info;
info._ch = _infos[i]._ch;
info._count = _infos[i]._count;
printf("codec ch:%u, cout:%u\n", (unsigned char)info._ch, info._count);
fwrite(&info, objSize, 1, fin); // 将对应的码流信息写入
writeNum++;
}
}
TmpInfo info;
info._count = -1;
printf("code objSize:%d\n", objSize);
fwrite(&info, objSize, 1, fin); //把info._count = -1写进去作为结束标志位
//3.压缩
int writeCount = 0;
int readCount = 0;
fseek(fout, 0, SEEK_SET); //文件指针、偏移量、参照位置
ch = fgetc(fout);
readCount++;
unsigned char value = 0;
size_t pos = 0;
while (feof(fout) == 0) // 一个个字符读取,效率虽然低一些,但不影响实验
{
// 读取数据,查找对应编码
string &code = _infos[(unsigned char)ch]._code; // 查找对应的编码
printf("code[%d]:%u:%s\n", readCount, (unsigned char)ch, code.c_str());
// code 实际存储的是对应 某个字符的哈夫曼编码
for (size_t i = 0; i < code.size(); ++i)
{
if (code[i] == '1')
value |= (1 << pos);
else if (code[i] == '0')
{
value &= ~(1 << pos);
}
else
{
assert(false);
printf("assert(false); ??????????");
}
++pos;
if (pos == 8)
{
writeCount++;
fputc(value, fin); // 够8个bit存储
value = 0;
pos = 0;
}
}
readCount++;
ch = fgetc(fout);
}
if (pos > 0)
{
writeCount++;
fputc(value, fin); //写入压缩文件(fin)
}
printf("huffman code table size::%d\n", objSize * (writeNum + 1));
printf("compress file data size:%d\n", writeCount);
unsigned long totalSize = writeCount + objSize * (writeNum + 1);
printf("compress file total size:%lu, orign file size:%lu, ratio:%0.2f\n",
totalSize, fileSize, (float)(totalSize*1.0/fileSize));
fclose(fout);
fclose(fin);
}
void Uncompress(const char *file)
{
string uncompressfile = file; //file:Input.txt.huffman
size_t pos = uncompressfile.rfind('.'); //找到倒数第一个'.'
assert(pos != string::npos);
uncompressfile.erase(pos); //删除掉'.'后面字符串
uncompressfile += ".unhuffman"; //Input.txt+'.unhuffman'
FILE *fin = fopen(uncompressfile.c_str(), "wb"); //打开解压缩文件
assert(fin);
FILE *fout = fopen(file, "rb"); //打开压缩文件
assert(fout);
//3.0 读入字符出现的信息
TmpInfo info;
int cycleNum = 1;
int objSize = sizeof(TmpInfo);
fread(&info, objSize, 1, fout);
while (info._count != -1) //-1为结束标志
{
// printf("decodec ch:%u, cout:%u\n", (unsigned char)info._ch, info._count);
_infos[(unsigned char)info._ch]._ch = info._ch;
_infos[(unsigned char)info._ch]._count = info._count;
fread(&info, objSize, 1, fout);
cycleNum++;
}
int aaa = 0;
//重建huaffman树
CharInfo invalid;
invalid._count = 0;
HuffmanTree tree(_infos, 256, invalid); //参数:数组,256个,无效值(出现0次)
Node *root = tree.GetRoot();
Node *cur = root;
CountType n = root->_weight._count; //所有叶子节点的和(源文件字符的个数)
char ch = fgetc(fout); //从fout(压缩文件)读字符
int readCount = 0;
while (ch != EOF || n > 0)
{
for (size_t i = 0; i < 8; ++i)
{
if ((ch & (1 << i)) == 0)
cur = cur->_pLeft; // 往左边找
else
cur = cur->_pRight; // 往右边找
if (cur->_pLeft == NULL && cur->_pRight == NULL)
{
//cout << cur->_weight._ch;
readCount++;
if(readCount % 1024 == 0)
{
// printf("uncompress %dk data\n", readCount/1024);
}
fputc(cur->_weight._ch, fin); //fin解压缩文件
cur = root;
if (--n == 0)
break;
}
}
ch = fgetc(fout);
}
printf("uncompress end\n");
fclose(fin);
fclose(fout);
}
protected:
CharInfo _infos[256];
};
#endif main.cpp
/*
* @Author: your name
* @Date: 2020-06-04 16:21:01
* @LastEditTime: 2020-06-04 19:13:01
* @LastEditors: Please set LastEditors
* @Description: In User Settings Edit
* @FilePath: \huffman\main.cpp
*/
/*利用库中的优先级队列实现哈夫曼树,最后基于哈夫曼树最终实现文件压缩。
描述:
1.统计文件中字符出现的次数,利用优先级队列构建Haffman树,生成Huffman编码。
构造过程可以使用priority_queue辅助,每次pq.top()都可以取出权值(频数)最小的节点。每取出两个最小权值的节点,就new出一个新的节点,左右孩子分别指向它们。然后把这个新节点push进优先队列。
2.压缩:利用Haffman编码对文件进行压缩,即在压缩文件中按顺序存入每个字符的Haffman编码。
3.将文件中出现的字符以及它们出现的次数写入配置文件中,以便后续压缩使用。
4.解压缩:利用配置文件重构Haffman树,对文件进行减压缩。
*/
#include "FileCompress.hpp"
#include
#include
#include
#include
// 注意是用g++编译器
// 编译 g++ -o huffman main.cpp HuffmanTree.hpp FileCompress.hpp -std=c++11
int main(int argc, char** argv)
{
if (argc != 2)
{
std::cout << "usage: " << argv[0] << ": " << std::endl;
return 1;
}
FileCompress fc;
FileCompress fc1;
std::string fileName(argv[1]);
fc.Compress(fileName.c_str()); // 压缩文件
fileName += ".huffman"; // 压缩后的文件名
fc1.Uncompress(fileName.c_str()); // 解压缩
return 0;
} g++ -o huffman main.cpp HuffmanTree.hpp FileCompress.hpp -std=c++11