2020南京大学软件学院夏令营模拟机试题集
此文主要为了方便【想要参加南京大学软件学院】的同学熟悉机试题目类型。不知是否由于今年特殊原因,今年南软的机试类型和以往(一道算法题,一道面向对象编程题)不同。
注:南软通知入营后,会加入一个群聊,群文件中有《南京大学软院夏令营机试练习指南》,里面有介绍机试的慕测平台,以及如何注册账号、练习、参加考试等等
1,字符串的修改
1)题目
题目描述
依旧是字符串处理,设A和B是两个字符串。我们要用最少的字符操作次数,将字符串A转换为字符串B。这里所说的字符操作共有三种:
- 删除一个字符;
- 插入一个字符;
- 将一个字符改为另一个字符。 对任给的两个字符串A和B,计算出将字符串A变换为字符串B所用的最少字符操作次数。
输入描述
第一行为字符串A;第二行为字符串B;字符串A和B的长度均小于200。输出描述
只有一个正整数,为最少字符操作次数。测试样例
输入
sfdxbqw
gfdgw
输出
4
2)解题思路
动态规划经典例题——最小编辑距离(暗示今年可能会有动态规划方面的题目)
参考@Mcosy【【动态规划】最小编辑距离(字符串A到字符串B变化最少要多少步)】(感谢博主分享!图片素材及主要思想来自此文)
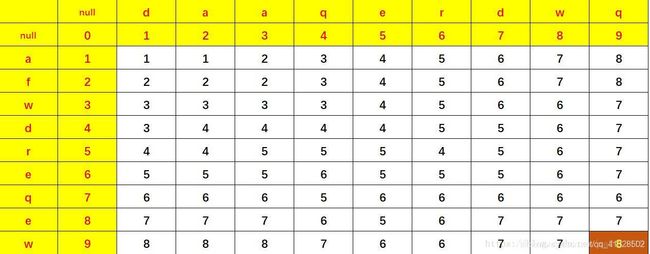
从字符串A"daaqerdwq"(横轴)到字符串B"afwdreqew"(纵轴),需经过最少的变换次数为8(棕色方框展示)
状态转移方程如下:
dp[i][j]=min(min(dp[i-1][j]+1,dp[i][j-1]+1),(A[j-1]==B[i-1]?dp[i-1][j-1]:dp[i-1][j-1]+1));- 由于从 字符串变为空 / 空变为字符串 只有单纯的 删除 / 添加 操作,所以dp[x][0]和dp[0][x]对应的最少操作次数,都是相应字符串位数;
- 由于字符串编号从0开始,而dp数组中对于字符串的处理从1开始(第0行,第0列有其他用途),所以A[j-1]对应的是A中第j个字符,B[i-1]同理;
- 计算dp[i][j]需要考虑三个位置的值,并选择最小值:
- dp[i-1][j]+1(字符串A[0,j-1]已经转换为字符串B[0,i-2],还需添加一个字符B[i-1]。比如daaqerdwq=》afwdreqew,再添加w即可)、
- dp[i][j-1]+1(字符串A[0,j-2]已经转换为字符串B[0,i-1],还需删去一个字符A[j-1]。比如daaqerdwq=》afwdreqew,再删除q即可)、
- dp[i-1][j-1]+(1/0)(当A[j-1]==B[i-1]时,可直接把A[j-2]转换为B[i-2]的操作次数dp[i-1][j-1],看作A[j-1]转换为B[i-1]的操作次数dp[i][j],否则只需将A[j-1]修改为B[i-1]即可。比如当A[j-1]不等于B[i-1]时,即daaqerdwq=》afwdreqew,q转换为w即可,dp[i][j] == dp[i-1][j-1]+1;当A[j-1]等于B[i-1]时,即daaqerdww=》afwdreqew,dp[i][j] == dp[i-1][j-1])。
3)AC代码(C++)
#include
using namespace std;
int getMinEditDis(string A, string B){
int lenA = A.length();
int lenB = B.length();
int dp[lenB + 1][lenA + 1]; //横轴原始字符串 纵轴目标字符串
dp[0][0] = 0;
for(int i = 1; i <= lenA; i++)
dp[0][i] = i;
for(int i = 0; i <= lenB; i++)
dp[i][0] = i;
for(int i = 1; i <= lenB; i++){ //i行对应linB j列对应lenA
for(int j = 1; j <= lenA; j++){
dp[i][j] = min(min(dp[i - 1][j] + 1, dp[i][j - 1] + 1), A[j - 1] == B[i - 1] ? dp[i - 1][j - 1] : dp[i - 1][j - 1] + 1);
}
}
return dp[lenB][lenA];
}
int main(){
string A, B;
cin>>A>>B;
int ans = getMinEditDis(A, B);
cout<
2,字符串正反连接
1)题目
题目描述
所给字符串正序和反序连接,形成新串并输出输入描述
任意字符串(长度<=50)输出描述
字符串正序和反序连接所成的新字符串测试样例
输入
123abc
输出
123abccba3212)解题思路
getline(cin, String)读取数据(不能直接用cin,因为字符串中间可能含有空格)
然后字符串遍历拼接(String类型操作还是很方便的)
3)AC代码(C++)
#include
using namespace std;
int main(){
string A, B;
cin>>A;
B = A;
for(int i = A.length() - 1; i >= 0; i--){
B += A[i];
}
cout<
3,字符串的展开
1)题目描述
题目描述
如果在输入的字符串中,含有 类似于“d-h”或者“4-8”的字串,我们就把它当作一种简写,输出时,用连续递增的字母获数字串替代其中的减号,即,将上面两个子串分别输出为 “defgh”和“45678”。在本题中,我们通过增加一些参数的设置,使字符串的展开更为灵活。具体约定如下:
(1) 遇到下面的情况需要做字符串的展开:在输入的字符串中,出现了减号“-”,减号两侧同为小写字母或同为数字,且按照ASCII码的顺序,减号右边的字符严格大于左边的字符。
(2) 参数p1:展开方式。p1=1时,对于字母子串,填充小写字母;p1=2时,对于字母子串,填充大写字母。这两种情况下数字子串的填充方式相同。p1=3时,不论是字母子串还是数字字串,都用与要填充的字母个数相同的星号“*”来填充。
(3) 参数p2:填充字符的重复个数。p2=k表示同一个字符要连续填充k个。例如,当p2=3时,子串“d-h”应扩展为“deeefffgggh”。减号两边的字符不变。
(4) 参数p3:是否改为逆序:p3=1表示维持原来顺序,p3=2表示采用逆序输出,注意这时候仍然不包括减号两端的字符。例如当p1=1、p2=2、p3=2时,子串“d-h”应扩展为“dggffeeh”。
(5) 如果减号右边的字符恰好是左边字符的后继,只删除中间的减号,例如:“d-e”应输出为“de”,“3-4”应输出为“34”。如果减号右边的字符按照 ASCII码的顺序小于或等于左边字符,输出时,要保留中间的减号,例如:“d-d”应输出为“d-d”,“3-1”应输出为“3-1”。
数据规模和约定
100%的数据满足:1< =p1< =3,1< =p2< =8,1< =p3< =3。字符串长度不超过100
输入描述
输入包括两行:
第1行为用空格隔开的3个正整数,一次表示参数p1,p2,p3。
第2行为一行字符串,仅由数字、小写字母和减号“-”组成。行首和行末均无空格。 输出描述
输出只有一行,为展开后的字符串。 测试样例
输入
1 2 1
abcs-w1234-9s-4zz
输出
abcsttuuvvw1234556677889s-4zz2)解题思路
类似于这种条件非常复杂的情况,我比较喜欢的做法是自顶向下,从主函数入手,看需要辅助函数得到什么样的结果,先把函数接口和输出接口定义好,便假定这个函数已经得到了我想要的东西,于是接着往下写。在构造辅助函数时,原理同上。
比如:
- 主函数:针对小的题目,由于不需要考虑参数在整个工程中的复杂关系,这里为了使函数参数列表看起来不那么臃肿,将输入字符串以及参数p1, p2, p3当作全局变量。而且我希望通过unford()函数得到完全处理后的字符串,于是就有了ans = unford();
- string unford():我要得到完全处理后的字符串,那么需要判断当前字符是否需要扩展needUnford,以及得到扩展后的字符串unfordString;
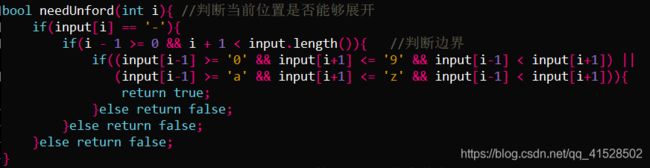
- bool needUnford(int i):希望通过此函数判断是否需要扩展;
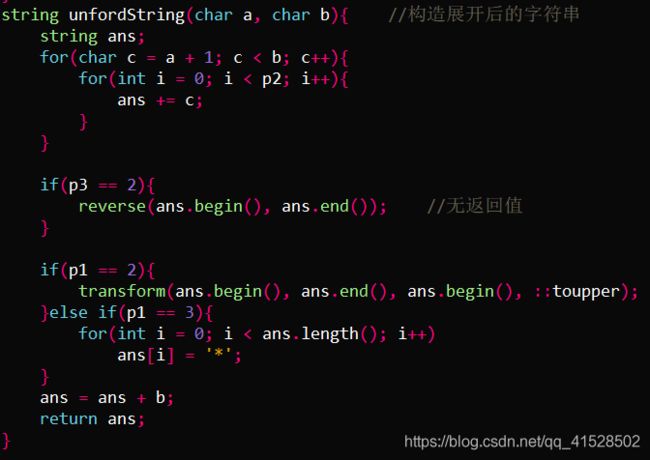
- string unfordString(char a, char b):希望通过此函数获得扩展部分的字符串,根据参数处理字符串即可;
3)AC代码(C++)
//#include
#include
#include
#include
using namespace std;
int p1, p2, p3;
string input;
bool needUnford(int i){ //判断当前位置是否能够展开
if(input[i] == '-'){
if(i - 1 >= 0 && i + 1 < input.length()){ //判断边界
if((input[i-1] >= '0' && input[i+1] <= '9' && input[i-1] < input[i+1]) ||
(input[i-1] >= 'a' && input[i+1] <= 'z' && input[i-1] < input[i+1])){
return true;
}else return false;
}else return false;
}else return false;
}
string unfordString(char a, char b){ //构造展开后的字符串
string ans;
for(char c = a + 1; c < b; c++){
for(int i = 0; i < p2; i++){
ans += c;
}
}
if(p3 == 2){
reverse(ans.begin(), ans.end()); //无返回值
}
if(p1 == 2){
transform(ans.begin(), ans.end(), ans.begin(), ::toupper);
}else if(p1 == 3){
for(int i = 0; i < ans.length(); i++)
ans[i] = '*';
}
ans = ans + b;
return ans;
}
string unford(){
string ans;
for(int i = 0; i < input.length(); i++){
if(needUnford(i)){
ans += unfordString(input[i-1], input[i+1]);
i++; //跳过 '-'后一个字符
}else{
ans += input[i];
}
}
return ans;
}
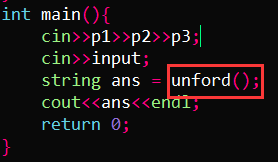
int main(){
cin>>p1>>p2>>p3;
cin>>input;
string ans = unford();
cout< 4,切开字符串
1)题目描述
Pear用如下方式评估切割的方案: 定义“正回文子串”为:长度为奇数的回文子串。 设切成的两段字符串中,前一段中有A个不相同的正回文子串,后一段中有B个不相同的非正回文子串,则该方案的得分为A*B。
注意,后一段中的B表示的是:“...非正回文...”,而不是: “...正回文...”。 那么所有的切割方案中,A*B的最大值是多少呢?
输入描述
输入第一行一个正整数N(<=10^5)
接下来一行一个字符串,长度为N。该字符串仅包含小写英文字母。输出描述
一行一个正整数,表示所求的A*B的最大值。测试样例
输入
10
bbaaabcaba
输出
382)解题思路
参考@ChiselStone【蓝桥杯-切开字符串】,文章中通过实例对算法进行讲解,过程很详细。
注意子串的概念!比如abc的子串为a, ab, abc, b, bc, c;
基本思想是:遍历字符串中每一个位置,将其分为两部分,左边统计正回文子串数目,右边统计非正回文数目,存入echoNum和notEchoNum数组中,最后遍历这两个数组求得相应位置乘积,取得最大值;
利用集合set
正回文子串:
b b a a a b c a b a
1 1 2 2 3 4 5 5 5 6
非正回文子串:
b b a a a b c a b a
39 30 24 19 13 9 5 2 1 0
3)AC代码(C++)
//#include
#include
#include
#include
#include
using namespace std;
set echo, notEcho;//当前字符串所有字串含有的回文/非回文子串
bool isEcho(string s){
if(s.length() % 2 != 1){
return false;
}else{
for(int i = 0; i < s.length() / 2; i++){
if(s[i] != s[s.length() - 1 - i]){
return false;
}
}
return true;
}
}
int main(){
int n, echoNum[100010], notEchoNum[100010];
string input, temp;
cin>>n>>input;
for(int i = 0; i < n; i++){ // 自左向右 统计位置0到i为止 所有正回文子串数目
for(int j = 0; j <= i; j++){
temp = input.substr(j, i - j + 1);
if(isEcho(temp)){
echo.insert(temp);
}
}
echoNum[i] = echo.size();
}
for(int i = n - 1; i >= 0; i--){ // 自右向左 统计位置i到n-为止 所有非正回文子串数目
for(int j = i; j < n; j++){
temp = input.substr(i, j - i + 1);
if(!isEcho(temp)){
notEcho.insert(temp);
}
}
notEchoNum[i] = notEcho.size();
}
int ans = 0;
for(int i = 0; i < n - 1; i++){ // 划分的两部分均不能为空 所以只到n-1
ans = max(ans, echoNum[i] * notEchoNum[i+1]);
}
cout<
5,正则表达式
1)题目描述
题目描述
给出一个非空的正则表达式和一个字符串,求该字符串是否能匹配该正则表达式。
这个正则表达式可能含有:
基本元素:
空串,输入中不体现;
单个小写字母(例如 a ),a 匹配小写字母 a,这里 a 表示小写字母 a。
运算符:
连接(例如 ab),ab 匹配可以表示成一个与 a 匹配的串与一个与 b 匹配的串相连接的串,这里 a 表示一个正则表达式,下同。
或(例如 a|b),a|b 匹配与 a 和 b 中至少一个匹配的串。
闭包(例如 a),a 匹配零个或多个与 a 匹配的串的连接。
正闭包(例如 a+),a+ 匹配一个或多个与 a 匹配的串的连接。
括号(例如 (a))
其中连接和或是二元运算符,闭包和正闭包是一元运算符。
所有运算符都是左结合的,即同等优先级的运算顺序从左到右。
闭包和正闭包的优先级最高,连接次之,或的优先级最低。
输入描述
多组数据,每组数据两行:
第一行是一个非空正则表达式,保证符合上述定义,但可能出现多余括号。保证不出现空括号。
第二行是一个由小写字母组成的非空字符串。输出描述
对于每组数据,如果正则表达式能匹配该字符串,输出一行 "Yes",否则输出一行 "No",不含引号。测试样例
输入
aa
a
a*
aa
a+
a
c*a*b
aab
ab*a
bbb
a(a|b+)*a
aa
a(a|b+)*a
aababba
a(a|cb+)*a
aca
a(a|cb+)*a
acbbbaacba
a(a|cb+)*a
acbbbaacb
((a*))
aa
输出
No
Yes
Yes
Yes
No
Yes
Yes
No
Yes
No
Yes2)解题思路
这一题要用到有限自动机相关的知识,且较为复杂,这里就不再介绍了