线段树入门学习总结
**
线段树
线段树是一种二叉搜索树,与区间树相似,它将一些区间划分成一些单元区间,每个单元区间对应线段树上的一个叶节点。
对于线段树中每个非叶子结点【a,b】,他的左儿子表示的区间为【a,(a+b)/2】,右儿子表示的区间【(a+b)+1,b】,因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
其时间复杂度为O(m*logN).
线段树有很多模板,基本上每道题都是稍微改下或者不用改就可以使用。
例题1
CDUTCM1584忠诚
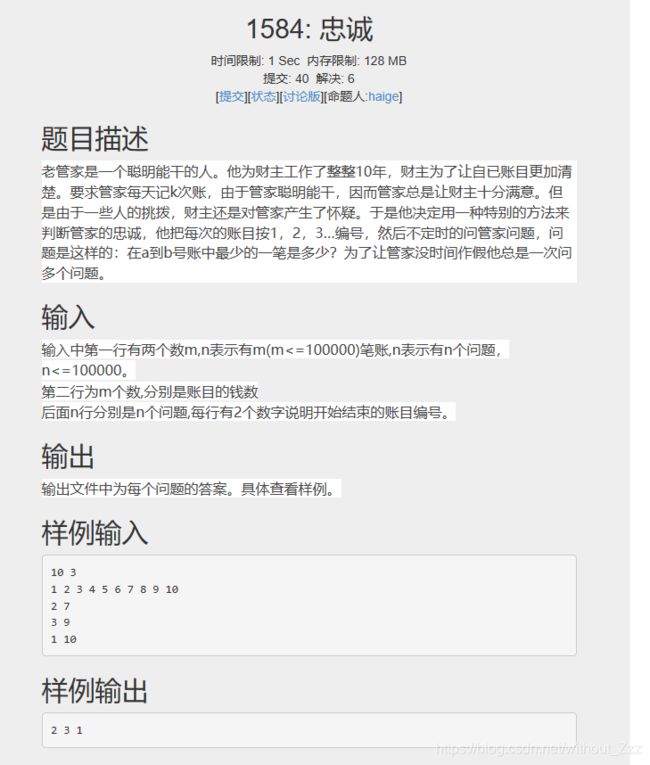
最简单的模板题,直接用模板即可
#include#include !!!)
#define SIZE 400010 // 数组大小,在线段树问题中一般是数据个数的四倍
#define INF 2e+09 // 用一个很大的数 (如 2e+09, 或2 000 000 000) 来表示无穷大
using namespace std; // 使用标准 (std) 命名空间
int res[SIZE]; // 存储区间的最小值,下标是对应节点的代号
void buildtree(int pos, int l, int r) // 建一颗线段树
// pos : 当前节点的代号
// l : 当前区间的左端
// r : 当前区间的右端
// 该函数的时间复杂度 : O (n)
{
int mid;
if (l == r) // 此区间只有一个数!
{
scanf("%d", &res[pos]); // 直接把这个数据给输入了
return; // 直接溜走
}
mid = l + r >> 1; // 得到区间的中间点mid
buildtree(pos << 1, l, mid); // 建造表示该区间左半段的树
buildtree((pos << 1) + 1, mid + 1, r); // 建造表示该区间右半段的树
res[pos] =min(res[pos<<1], res[(pos<<1)+1]); // 当前区间最小值取该区间左半段和该区间右半段最小值的最小值
return;
}
void update(int pos, int l, int r, int x, int y) // 更新一个点的值
// pos : 当前节点的代号
// l : 当前区间的左端
// r : 当前区间的右端
// x : 要改变的数的下标
// y : 要把那个数改为y
// 该函数的时间复杂度 : O (log2 n)
{
int mid;
if (l == r) // 该区间只有一个数,也就是说找到了要改变的那个数!
{
res[pos] = y; // 直接改变该数的值
return; // 直接溜了
}
mid = l + r >> 1; // mid表示该区间的中间点
if (x <= mid) // 如果要改变的点在该区间的左半段
{
update(pos << 1, l, mid, x, y); // 那么,就在该区间的左半段寻找要改变的数
}
else // 否则,要改变的点在该区间的右半段
{
update((pos << 1) + 1, mid + 1, r, x, y); // 那么,就在该区间的右半段寻找要改变的数
}
res[pos] = min(res[pos<<1], res[(pos<<1)+1]); // 由于这个区间的左半段或者右半段的最小值已经被改变,需要更新该区间的最小值
return;
}
int query(int pos, int l, int r, int x, int y) // 询问区间 [x, y] 中的最小值
// pos : 当前节点的代号
// l : 当前区间的左端
// r : 当前区间的右端
// x : 要查询最小值的区间的左端
// y : 要查询最小值的区间的右端
// 该函数时间复杂度 : O (log2 n)
{
int t1, t2, mid;
if ((r < x) || (l > y)) // 此区间和要询问的最小值的区间 [x, y] 没有重合部分
{
return INF; // 直接开溜
}
if ((x <= l) && (y >= r)) // 此区间完全包含在要询问最小值的区间 [x, y] 中
{
return res[pos]; // 直接返回
}
mid = l + r >> 1; // mid表示该区间的中间点
t1 = t2 = INF; // 这样做是为了不符合下一步递归条件的值设为无穷大 (INF)
if (x <= mid) // 如果该区间的左半段 [l, mid] 和要询问最小值的区间 [x, y] 有重合部分
{
t1 = query(pos << 1, l, mid, x, y); // 在该区间的左半段 [l, mid] 寻找答案
}
if (y > mid) // 如果该区间的右半段 [mid + 1, r] 和要询问最小值的区间 [x, y] 有重合部分
{
t2 = query((pos << 1) + 1, mid + 1, r, x, y); // 在该区间的右半段 [mid + 1, r] 寻找答案
}
return min(t1, t2); // 返回该区间的左半段的答案和右半段的答案的最小值
}
int main(void) // 终于到主函数了!
{
int n, m, p, x, y;
scanf("%d%d", &n, &m); // 输入数据数目以及操作个数
buildtree(1, 1, n); // 建一颗线段树,顺便输入数据
while (m--)
{
scanf("%d%d%d", &p, &x, &y); // 输入操作编号和操作参数
if (p == 1)
{
printf("%d ", query(1, 1, n, x, y)); // 询问区间的最小值
}
else
{
update(1, 1, n, x, y); // 更新一个数据
}
}
return 0;
}
例题3
#include其实线段树这种算法主要是要学会用模板就可以了
**

