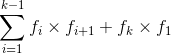hdu5448(三角剖分+前缀和)

题意：按逆时针给定一个凸多边形上的点，选取若干个点形成凸包，这些所有凸包的面积之和的2倍

这个题以前就碰过，印象深刻（指标题），然后刚好看见tls写了这题的题解就瞄了一眼。。

其实。。就只是一个结论而已，一个三角剖分的应用。。

令原点和凸包的顶点（逆时针排列）构成的向量分别为，

那么利用三角剖分该凸包的面积可以表示为

然后就直接考虑的贡献就可以了，演着i->j这个方向至少要有一个点和他构成凸包，所以有

然后求个前缀和就能降成O(n)

 

 

 

/**
 *　　　　　　  　　┏┓　　 　┏┓
 * 　　　　　  　　┏┛┗━━━━━━━┛┗━━━┓
 * 　　　　　  　　┃　　　　　　　┃ 　
 * 　　　　　  　　┃　　　━　　 　┃
 * 　　　　　  　　┃　＞　　　＜　┃
 * 　　　　　  　　┃　　　　　　　┃
 * 　　　　　  　　┃...　⌒　... 　┃
 * 　　　　　　  　┃              ┃
 * 　　　　　　  　┗━┓          ┏━┛
 * 　　　　　　　　　┃          ┃　Code is far away from bug with the animal protecting　　　　　　　　　　
 * 　　　　　　　　　┃          ┃   神兽保佑,代码无bug
 * 　　　　　　　　　┃          ┃　　　　　　　　　　　
 * 　　　　　　　　　┃          ┃  　　　　　　
 * 　　　　　　　　　┃          ┃
 * 　　　　　　　　　┃          ┃　　　　　　　　　　　
 * 　　　　　　　　　┃          ┗━━━┓
 * 　　　　　　　　　┃              ┣┓
 * 　　　　　　　　　┃              ┏┛
 * 　　　　　　　　　┗┓┓┏━━━━━━━━┳┓┏┛
 * 　　　　　　　　　　┃┫┫       ┃┫┫
 * 　　　　　　　　　　┗┻┛       ┗┻┛
 */ 
#include
#include
#include
#include
#include
#include

 

 

 

 

Marisa’s Cake

Time Limit: 3000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 340    Accepted Submission(s): 198

 

Problem Description

Today is Marisa’s birthday and she is given a cake the shape of a convex polygon of n vertices. Furthermore, all the n vertices are all going to be on integer points of the Cartesian coordinate system. Marisa asks her friend Reimu to randomly cut off some vertices of the cake. The set of vertices chosen to be cut off has size at most n−3, and all possible choices have the same probability to be picked up. In order to remove all chosen vertices, Reimu might cut the cake several times. Since Reimu is a perfectionist, she will always cut the cake from one vertex to another. Hence, Reimu’s cutting will not generate vertices which are not in the original polygon.

Marisa wants to know the expected size of the cake she might get, and because you are madly in love with her, you decided to do anything she wants for her! You take out your laptop and are ready to calculate the expected size for Marisa. However, Marisa is bad with fractions. She wants to make sure the answer she gets is always an integer. To do that, she would like you to multiply the answer with the total number of possible cakes there are. Unfortunately, that still doesn’t guarantee the answer be an integer. An additional 2 must also be multiplied into the answer as well. For example, let A=(0,0),B=(1,0),C=(1,1),D=(0,2) and ABCD is the shape of Marisa’s birthday cake. There are 5 possible pieces ABCD,ABC,BCD,CDA,DAB that Marisa might get, and the corresponding area of these convex polygons are 32,12,12,1,1 respectively. The expected size of the cake that Marisa might get is (32+12+12+1+1)÷5=910 , and what you should tell Marisa 910×5×2=9. Calculate the answer for Marisa and who knows, maybe she would love you back!

 

 

Input

The first line on the input contains an integer T(T≤10). There will be T test cases. The first line of each test case contains an integer n(3≤n≤100000) indicating the number of vertices of the convex polygon. The i−th of the following n lines contains two integers xi and yi(0≤x,y≤109) separated by a blank. (xi,yi) is the i−th vertex of the convex polygon, and (x1,y1),...,(xn,yn) will be in counterclockwise order.

 

 

Output

For each test case, output a number as the answer. In case the answer is greater than 1000000006, please modulo the answer with 1000000007. (You might figure out by now that Marisa is not good at dealing with large numbers either)

 

 

Sample Input

2 4 0 0 1 0 1 1 0 2 5 1 1 3 1 3 2 2 3 1 2

 

 

Sample Output

9 50

 

 

Source

2015 ACM/ICPC Asia Regional Changchun Online

 

 

Recommend

hujie   |   We have carefully selected several similar problems for you:  6460 6459 6458 6457 6456 

 

 

Statistic | Submit | Discuss | Note