状压DP学习总结 (详解,适合没状压dp基础的人学习,还在更新中,,,,)
本次博客,主要是给学弟学妹们讲解一下状压dp,不适合有基础的同学观看,可能会浪费时间,因为偏基础
先来最简单的一个吧 http://acm.hdu.edu.cn/showproblem.php?pid=1565 hdu 1565
方格取数(1)
Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 11722 Accepted Submission(s): 4391
Problem Description
给你一个n*n的格子的棋盘,每个格子里面有一个非负数。
从中取出若干个数,使得任意的两个数所在的格子没有公共边,就是说所取的数所在的2个格子不能相邻,并且取出的数的和最大。
Input
包括多个测试实例,每个测试实例包括一个整数n 和n*n个非负数(n<=20)
Output
对于每个测试实例,输出可能取得的最大的和
Sample Input
3 75 15 21 75 15 28 34 70 5
Sample Output
188
首先我们如果不考虑不能取连续的两个数,那么就像是一个数塔一样最简单的dp模型了,相邻的两个数不能取,我们要先理解最基本的状态,在类似状压bfs的时候也可以类比出来,再推一道很基本的状压bfs:http://acm.hdu.edu.cn/showproblem.php?pid=1429
那么我们可以对每一列,设为二进制状态,因为n比较少,最多也就(1 << 17)
如果第i行状态为11001,那么说明我们第i行取得是1,4,5位置,那么对于第i行我们可以取这个状态,只与第i - 1行取得什么状态有关,如果第i - 1行的状态为y,要取第i行为x,那么一定要(x & y) == 0才满足不取相邻的两个(具体就是二进制位上不能有相同的1,利用&的特性,很容易理解),方程也很容易可以得到f[i][j]代表第i行取j这个状态,然后可以枚举第i - 1行的状态,在枚举第i行的状态,并且不冲突即可。当然我们暴力枚举时间复杂度是多少呢?显然是n*(1 << n)*(1 << n) ,复杂度肯定会挂,然而我们还需要考虑,因为我们每一行对于这个状态,都不能有相邻的两个1,对吧?
所以需要我们需要保存一些合法的状态,这个可以打表看一下最多有多少个(其实这个n根本就没有20,不然平方级别17000 * 17000 * 20还可以过5s么,亲测了一下,n只有16)
所以就是 2584 * 2584 * 16,所以复杂度现在就解决了,至于去除不合法的状态,就很简单了,(i & (i >> 1) )== 0则证明是合法状态,因为i往后搓一位后,如果还没有和i有重叠的1,那肯定都是合法的。
代码:
int a[19][1 << 17];
int f[19][1<<17];
int tot[maxn];
int calc(int i,int x){
int cnt = 1,res = 0;
while(x){
if(x & 1) res += a[i][cnt];
x /= 2;cnt++;
}
return res;
}
int main()
{
ios::sync_with_stdio(false);
int n;
while(cin >> n){
// if(n >= 17){ while(1){ } }
int cnt = 0,ans = 0;
for(int i = 0;i < (1 << n);i++) if((i & (i >> 1)) == 0) tot[++cnt] = i;
for(int i = 1;i <= n;i++) for(int j = 1;j <= n;j++) cin >> a[i][j];
MS0(f);
for(int i = 1;i <= n;i++){
for(int k = 1;k <= cnt;k++){
int val = calc(i,tot[k]);
for(int j = 1;j <= cnt;j++){
if((tot[j] & tot[k]) == 0){
f[i][k] = max(f[i][k],f[i - 1][j] + val);
}
}
}
}
for(int j = 1;j <= cnt;j++) ans = max(ans,f[n][j]);
cout << ans << endl;
}
return 0;
}
另外学习了上面的题,再来一个类似的, poj 1185 http://poj.org/problem?id=1185
炮兵阵地
| Time Limit: 2000MS | Memory Limit: 65536K | |
| Total Submissions: 34387 | Accepted: 13208 |
Description
司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队。一个N*M的地图由N行M列组成,地图的每一格可能是山地(用"H" 表示),也可能是平原(用"P"表示),如下图。在每一格平原地形上最多可以布置一支炮兵部队(山地上不能够部署炮兵部队);一支炮兵部队在地图上的攻击范围如图中黑色区域所示:
![]()
如果在地图中的灰色所标识的平原上部署一支炮兵部队,则图中的黑色的网格表示它能够攻击到的区域:沿横向左右各两格,沿纵向上下各两格。图上其它白色网格均攻击不到。从图上可见炮兵的攻击范围不受地形的影响。
现在,将军们规划如何部署炮兵部队,在防止误伤的前提下(保证任何两支炮兵部队之间不能互相攻击,即任何一支炮兵部队都不在其他支炮兵部队的攻击范围内),在整个地图区域内最多能够摆放多少我军的炮兵部队。
Input
第一行包含两个由空格分割开的正整数,分别表示N和M;
接下来的N行,每一行含有连续的M个字符('P'或者'H'),中间没有空格。按顺序表示地图中每一行的数据。N <= 100;M <= 10。
Output
仅一行,包含一个整数K,表示最多能摆放的炮兵部队的数量。
Sample Input
5 4
PHPP
PPHH
PPPP
PHPP
PHHP我们再看这个题,只有P位置才可以放炮台,并且其他位置距离2的位置都会被占领,和刚刚的题很类似,刚刚的第i行只和i - 1有关,这个则与i - 1和i - 2有关,显然就多了以一维dp,那还是首先把所有合法的状态找出来,和刚刚的一样操作,定义f[i][j][k]状态为:第i行状态为j,第i - 1行状态为k的能放炮兵的个数。现在就又可以枚举第i行的第j个状态,另外再接着枚举第i - 1行的状态和第i - 2行的状态,首先先要check(j)这个状态是不是合法的,这个合法代表的是选取的每一位是否和第i行的位置对应并且他们都有p,或者这个状态是所有p的子集,一种方法,暴力挨个位数判断,那我们对于每个状态都要判断,第i、i - 1、i - 2,所以就会再复杂度上再加上一个级别
现在我们考虑怎么优化,我们可以把第i行的状态预处理出来,即有P的地方都变为1,处理出op[i],代表第i行的全集,那么op[i] & j 如果>0则可以表示与第i行的P的位置有冲突 其他的i - 1和i - 2一样的道理
那么我们可以列出方程
j 为 第i行的状态,k为第i - 1行的状态,p为i - 2行的状态,num则是j状态1的个数,就是选了多少个P,对于这个num,我们可以用暴力算出二进制1的个数从而得来,但是我们对这里也可以进行一个优化
f[i][j][k] = max(f[i][j][k],f[i - 1][k][p] + num)
现在问题就来到了能不能O1时间内得到x的二进制1的个数,那么我们可以根据树状数组的lowbit(x)在O1时间内得到x的末尾0的个数(当然这个(x&(-x))是真的太神奇了),现在我们可以枚举状态到(1 << m),假设
101100这个1的个数显然可以从101的1的个数+1得来,所以我们可以到i - lowbit(i)得到101的1的个数,并且101的个数是以及枚举过得
代码:
char str[190][1 << 10];
int f[190][80][80];
int tot[maxn];
//int f[i][j][k];///第i行,第i行取的状态是j,第i - 1行取得状态是k
int op[maxn];
int num[maxn];
int main()
{
// ios::sync_with_stdio(false);
int n,m;
cout << lowbit(3) << endl;
while(cin >> n >> m){
int cnt = 0;
for(int i = 1;i <= n;i++) scanf("%s",str[i]);
for(int i = 0;i < (1 << m);i++) if(((i & (i >> 2)) == 0) && (i & (i >> 1)) == 0) tot[++cnt] = i;
for(int i = 1;i < (1 << m);i++) {
num[i] = num[i - lowbit(i)] + 1;
cout << lowbit(i) << " ";
cout << i <<" " << i - lowbit(i) << " " << num[i] <= 2 && (tot[k] & op[i - 1]))continue;
for(int p = 1;p <= cnt;p++){///枚举第i - 2的状态
if(tot[p] & op[i - 2]) continue;
if((tot[p] & tot[k]) == 0 && (tot[j] & tot[p]) == 0) f[i][j][k] = max(f[i][j][k],f[i - 1][k][p] + val);
}
ans = max(f[i][j][k],ans);
}
}
}
cout << ans << endl;
}
return 0;
}
最后再来一个例子吧 uva11825
https://uva.onlinejudge.org/index.php?option=com_onlinejudge&Itemid=8&page=show_problem&problem=2925
Miracle Corporations has a number of system services running in a distributed computer system which
is a prime target for hackers. The system is basically a set of N computer nodes with each of them
running a set of N services. Note that, the set of services running on every node is same everywhere
in the network. A hacker can destroy a service by running a specialized exploit for that service in all
the nodes.
One day, a smart hacker collects necessary exploits for all these N services and launches an attack
on the system. He finds a security hole that gives him just enough time to run a single exploit in each
computer. These exploits have the characteristic that, its successfully infects the computer where it
was originally run and all the neighbor computers of that node.
Given a network description, find the maximum number of services that the hacker can damage.
Input
There will be multiple test cases in the input file. A test case begins with an integer N (1 ≤ N ≤ 16),
the number of nodes in the network. The nodes are denoted by 0 to N − 1. Each of the following
N lines describes the neighbors of a node. Line i (0 ≤ i < N) represents the description of node i.
The description for node i starts with an integer m (Number of neighbors for node i), followed by m
integers in the range of 0 to N − 1, each denoting a neighboring node of node i.
The end of input will be denoted by a case with N = 0. This case should not be processed.
Output
For each test case, print a line in the format, ‘Case X: Y ’, where X is the case number & Y is the
maximum possible number of services that can be damaged.
Sample Input
3
2 1 2
2 0 2
2 0 1
4
1 1
1 0
1 3
1 2
0
Sample Output
Case 1: 3
Case 2: 2
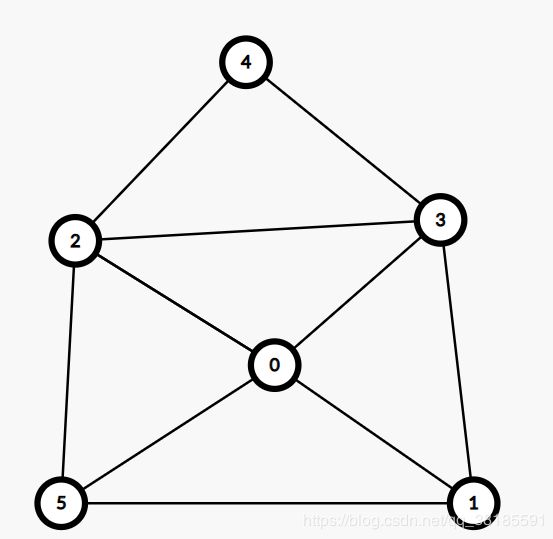
仔细读题,题意描述有点怪,其实就是给你第i个点和与他相邻的点,让你求出他可以最多有多少个没有任何交集的集合,使得任意集合的所有点再加上相邻的点,从而覆盖全部的图,问你最多可以有多少个这样的集合
对于下面这个图,那他就可以找出3个集合,分别是
{4,0}、{3,5}、{1,2}
对这种,我们显然是肯定可以枚举他的子集的,并且再去找与他不相交的集合里,能不能构成覆盖所有点的条件
我们就可以针对n来枚举子集,看下面这个dfs函数,n代表我取得状态,然后我们再去枚举n的子集,那么枚举n的子集需要多少复杂度呢,最明显的可以用枚举所有状态&n,判断他是不是n的子集,并且再考虑计算,这样的话,复杂度就是2^n,我们最外层枚举n的所有状态又是2^n,这样就得到了4^n,n = 16,所以是不可行的,虽然有的地方我们可以加一个记忆化,但是复杂度还是通过不了的(dfs的复杂度可能不好计算,下面还有一个递推方式的写法)
int dfs(int n){
if(f[n] != -1) return f[n];
int ans = 0;
for(int i = n;i;i = ((i - 1) & n)) if(check(j)) ans = max(ans,dfs(i ^ n) + 1);
return f[n] = ans;
}
for(int i = 0; i < (1 << n);i++){
int ans = 0;
for(int j = i;j;j = (j - 1) & i){
if(check(j)){
ans = max(ans,f[i ^ j] + 1);
}
}
f[i] = ans;
}
现在我们来考虑怎么优化,怎么快速的找到i的子集呢,假如我们枚举所有的状态, 那么就会出现很多浪费枚举的时候,所以我们可以用一个特别巧妙地方法我们知道 i & n == i 是用来判断i是否是n的子集的(具体是为什么,写一下就知道了),那我们如果想枚举完i的子集,我们可以还是通过i--,来找到i的下一个最近的状态,但是这个i不一定是n的子集,所以我们可以用上面判断的方法来得到最近的符合是n的子集的状态,那就是(i - 1) & n,实在理解不了,就记下来吧。那这样可以优化多少时间复杂度呢
我们来看递推的dp复杂度,观察第一层for是2^n的复杂度,第2层for是只跟集合的大小有关系的,那么就是有
C(n,1) + C(n,2) + .... = ,这样的话,我们考虑大小为i的集合,就有2^i个子集, 那我们现在一起来考虑整个两层for循环的复杂度,就是∑C(n,i) * 2 ^ i,有没有发现这个东西很熟悉,那就是二项式定理了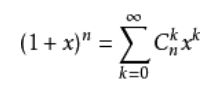
所以 ∑C(n,i) * 2 ^ i = 3 ^ i,大小为n的集合就是 3 ^ n,所以现在复杂度就有了
那我们的check要怎么写的呢,要在O1时间内,check出当前选的状态,可以覆盖完所有的图
首先我们可以对他输入的边进行处理,因为他出的是第i个点和哪些点有边,所以我们可以先预处理出一个p数组,表示选择i点可以与那些点相连,就是p[i] |= (1 << x),然后我们再来枚举0到(2^n)- 1的所有状态,定义一个arr数组,arr[i],i这个状态可以达到的点都有谁,对于每个状态,我们看看选了哪些点j,arr[i] |= p[j] ,就可以得到当前i状态可以达到的所有点的状态,那判断的时候,arr[i] == (1 << n) - 1 就可以表示所有的图的点都可以被覆盖了
代码:
int f[maxn];int k;
int p[maxn],arr[maxn];
int dfs(int n){
if(f[n] != -1) return f[n];
int ans = 0;
for(int i = n;i;i = ((i - 1) & n)) if(arr[i] == ((1 << (k)) - 1)) ans = max(ans,dfs(i ^ n) + 1);
return f[n] = ans;
}
int main()
{
int n;
int cas = 1;
while(cin >> n){
k = n;
if(n == 0) break;
MS1(f); MS0(p);MS0(arr);
int m,x;
for(int i = 0;i < n;i++){
cin >> m;
p[i] = (1 << i);
for(int j = 1;j <= m;j++){
cin >> x;
p[i] |= (1 << x);
}
}
for(int i = 0; i < (1 << n);i++){ ///2 ^ n
for(int j = 0;j < n;j++){
if(i & (1 << j)) arr[i] |= p[j];
}
}
/**
for(int i = 0; i < (1 << n);i++){
int ans = 0;
for(int j = i;j;j = (j - 1) & i){
if(arr[j] == (1 << n) - 1){
ans = max(ans,f[i ^ j] + 1);
}
}
f[i] = ans;
}
*/
dfs((1 << n)- 1);
printf("Case %d: %d\n",cas++,f[(1 << n) - 1] );
}
return 0;
}